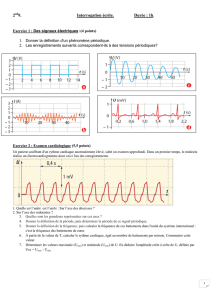
Redressement d`une tension rectangulaire ou sinusoïdale

TD: Redressement d’une tension rectangulaire ou sinuso¨ıdale
1 Position du probl`eme
L’´electricit´e nous est fournie par l’EDF sous forme d’une tension sinuso¨ıdale. Or, un grand nombre des
usages du courant ´electrique n´ecessite une tension continue. Le but de cet exercice est de d´eterminer et de
simuler les op´erations de transformation n´ecessaires.
CR
r
V U
1. ´ Etude en signaux carr´es.
On consid`ere le montage ci-dessus. Il est aliment´e par un g´en´erateur Vde p´eriode 50 Hz dont la tension
est V0si t∈[0, T/2], puis −V0si t∈[T/2, T ],. . . avec V0= 1 V.
La diode (D) ne laisse passer le courant que si V≥U.R= 1000 Ω repr´esente le circuit d’utilisation; rest
une petite r´esistance repr´esentant les caract´eristiques de la diode (r= 20 Ω).
a. Que vaut Upendant une p´eriode ? On distinguera les deux demi-p´eriodes.
b. Calculer la tension maximale Umax et minimale Umin.
c. On d´efinit le taux d’ondulation par: τ=Umax −Umin
Umax +Umin . Calculer τpour C= 10 µF, puis C= 100 µF.
2. ´ Etude en signaux sinuso¨ıdaux.
Le g´en´erateur est maintenant sinuso¨ıdal, de f.e.m. V=V0.cos(ω.t), avec V0= 1 V, la fr´equence ´etant
toujours 50 Hz.
a. ´ Ecrire l’´equation diff´erentielle v´erifi´ee par Ulorsque la diode conduit (V > U) et lorqu’elle est bloqu´ee.
b. ´ Ecrire le programme tra¸cant la courbe U(t).
c. Mesurer le taux d’ondulation τ, les valeurs de Umax et Umin. Pourquoi Umin est-il plus petit que dans
le cas des signaux carr´es ? On tracera les courbes pour C= 10 µF et C= 100 µF.
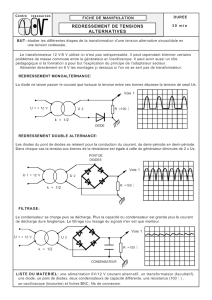
3. Am´elioration: redressement double alternance.
Dans le montage pr´ec´edent, la source est tr`es mal utilis´ee, car une seule fournit du courant au syst`eme.
Le sch´ema ci-dessous permet de profiter de chacune d’elles: si V > 0, D1 et D4 conduisent et la borne A
est positive.
r
VU
CR
D1 D2
D3 D4
A
Si V < 0, ce sont D2 et D3 qui conduisent et A est encore positive. tout se passe donc comme si l’on
alimentait le montage avec la tension |V0.cos(ω.t)|.
Tracer les courbes dans ce cas. Quel est le taux d’ondulation ? Comparer avec le cas pr´ec´edent.
1

ISEN-Brest. Kany. TD: Redressement d’une tension rectangulaire ou sinuso¨ıdale
Solution
1. a. Pendant la premi`ere demi-p´eriode o`u V−U > 0, la diode conduit: le courant dans la r´esistance Rest
U
R, celui dans le condensateur C.dU dt. La loi des nœuds donne: V−U r=U R+C. dU dt.
D’o`u: V=U.r+R
R+r.C. dU dt.
En posant k=r+R
r.R.C , la solution s’exprime sous la forme: U=V. R r+R+U1.e−k.t. Cette tension est
minimale `a t= 0:Umin 1=V. R
r+R+U1; elle est maximale pour t=T 2:Umax 1=V. R r+R+U1.e−k.T /2.
Pendant la deuxi`eme demi-p´eriode o`u V−U < 0, la diode bloque: le condensateur se d´echarge dans la
r´esistance R. On a: U=U2.e−
t−
T
2
(R.C). Cette tension est maximale `a t=T
2:Umax 2=U2et minimale
`a t=T:Umin 2=U2.e−
T
2
(R.C).
b. D’apr`es la continuit´e de la tension aux bornes du condensateur `a t=T
2:Umax 1=Umax 2et `a t=T:
Umin 2=Umin 1.
c. Pour C= 10 µF, Umin = 0,37 V, Umax = 1 V et τ= 0,46.
Pour C= 100 µF, Umin = 0,90 V, Umax = 1 V et τ= 0,05 (tension presque continue).
2. a. Les ´equations diff´erentielles sont inchang´ees.
Lorsque V−U > 0, la diode conduit: V=U.r+R
R+r.C. dU dtpour t∈[t0,T 2].
Lorsque V−U < 0, la diode bloque: U=U2.e−
t−t0
(R.C)pour t∈[T
2, T +t0].
c. Pour C= 10 µF, τ= 0,61; pour C= 100 µF, τ= 0,10. Les taux d’ondulation sont sup´erieurs car le
temps de charge du condensateur est inf´erieur `a T
2.
3. Pour C= 10 µF, τ= 0,29; pour C= 100 µF, τ= 0,04. Les taux d’ondulation sont inf´erieurs car le
condensateur se charge deux par p´eriode.
2 Code avec Mathematica
Redressement
Monoalternance
In[1]:= f=50;omega=N[2 Pi f];R=1000;r=20;Capa=.; T=1/f;V0=1;
•Cr´enaux
In[3]:= V[t ]:=If[Mod[t,T]<T/2,V0,-V0];
In[4]:= Equ[U ,t ,Capa ]:=( If[V[t]>U, (V[t]-U (r+R)/R)/(r Capa), -U/ (R Capa)])
In[5]:= Redressement[Capa ]:=( t=0; U=0;tmax=0.1;pas=0.00005;
Sol=Table[i,{i,0,tmax/pas}];i=0;
While[t<=tmax, U1=U+pas*Equ[U,t,Capa]; t1=t+pas;
U=U+pas*(Equ[U,t,Capa]+Equ[U1,t1,Capa])/2; i++;Sol[[i]]=U; t=t1;];
ListPlot[Sol,AxesOrigin->{0,0},PlotRange->{0,V0}]);
In[6]:= Redressement[10 10^-6]; Redressement[100 10^-6];
2

ISEN-Brest. Kany. TD: Redressement d’une tension rectangulaire ou sinuso¨ıdale
Out[7]=-Graphics-
•Sinuso¨ıde
In[8]:= V[t ]:=V0 Cos[omega t]; Redressement[10 10^-6]; Redressement[100 10^-6];
Out[9]=
Double alterance
•Sinuso¨ıde
In[11]:= V[t ]:=Abs[V0 Cos[omega t]]; Redressement[10 10^-6]; Redressement[100 10^-6];
Out[12]=
3 Code avec Python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
from pylab import mod
# Monoalternance
3

ISEN-Brest. Kany. TD: Redressement d’une tension rectangulaire ou sinuso¨ıdale
f=50;omega=2*np.pi*f;R=1000;r=20;T=1/f;V0=1;
#Cr´enaux
# Sinuso¨ıde
#Double alterance
# Sinuso¨ıde
4