TP C7 CHAMPS MAGNETIQUE ET GRAVITATIONNEL Objectifs

TP C7
CHAMPS MAGNETIQUE ET GRAVITATIONNEL
Objectifs:
 Cartographier un champ électrostatique
 Etudier le champ de pesanteur local
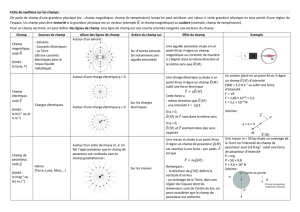
I. CHAMP MAGNETIQUE
1. Manipulations
Vous disposez d’un aimant droit, d’un aimant en U, d’aiguilles aimantées, une plaque contenant de petites aiguilles métalliques
et d’un tesla mètre permettant de mesurer la valeur du champ magnétique
Placer l’aimant droit sur la plaque. Noter vos observations et représenter la figure obtenue
Positionner les aiguilles aimantées à proximité de l’aimant, puis les déplacer le long des lignes formées. Noter vos
observations
Déplacer le tesla mètre autour de l’aimant, le long des lignes de champ. Noter vos observations
Répéter ces opérations avec l’aimant en U
2. Exploitation
1) Comment s’orientent les aiguilles aimantées en l’absence d’aimant ? Expliquer
2) Le champ créé par l’aimant est-il scalaire ou vectoriel ? Expliquer
3) Lorsque les lignes de champ se resserrent le champ magnétique est plus intense. Dans l’aimant en U, où le champ
magnétique est-il le plus intense ? Dans l’aimant droit ? Les mesures vérifient-elles cette affirmation ?
4) Lorsque les lignes de champ sont parallèles, le champ magnétique est uniforme. Quel(s) dispositif(s) permet(tent)
d’obtenir un champ magnétique uniforme. Situez le lieu du dispositif où cela se produit. Les mesures effectuées
confirment-elles cette affirmation ?
5) En un point M, le vecteur champ magnétique B a : pour direction la droite sud-nord de l’aiguille aimantée et pour sens
du nord vers le sud. Tracez les vecteurs champ magnétique.
6) Les lignes de champ et les vecteurs champ magnétique sont dans une disposition particulière. Laquelle ?
7) Les lignes de champ sont orientés dans le même sens que
B
. Placez des flèches montrant leur orientation.
8) Dans un aimant, on repère le pôle nord en rouge. Les lignes de champ sortent d’un pôle de l’aimant pour entrer dans
l’autre. Faîtes une phrase complète en indiquant clairement les pôles.

II. CHAMP DE PESANTEUR
1. Mesure du champ de pesanteur à l’aide d’un pendule simple
a. Principe
Un pendule simple est constitué d’un objet de petite dimension, de masse m, fixé à l’extrémité d’un fil inextensible de
longueur l. Il oscille sous l’effet du champ de pesanteur local
Pour de petites oscillations, la période T d’un pendule simple ne dépend que de la longueur l et de l’intensité du champ de
pesanteur local g0 : T = 2 l
g0
b. Expérience
Pour les différentes valeurs de l proposées, compléter le tableau :
l(m)
0,10
0,20
0,30
0,40
0,50
5T(s)
T(s)
T²(s²)
c. Exploitation
1) Pourquoi mesure-t-on 5 périodes et non une seule ?
2) Rentrer les valeurs l et T² dans le tableur de Latispro et tracer la courbe l = f(T²). Quel type de courbe obtient-on ?
3) Exprimer l en fonction de T²
4) A l’aide du tableur, déterminer la valeur de g0.
5) La valeur exacte du champ de pesanteur à Bourges étant g0th = 9,81 SI, déterminer l’écart relatif g0 = lg0-g0thl
g0th 100
2. Mesure de l’accélération de la pesanteur
a. Principe
Tout objet lâché chute verticalement en raison du champ de pesanteur qui règne à la surface de la Terre. Sa vitesse de
chute augmentant, l’objet en chute libre subit une accélération, appelée accélération de la pesanteur, correspondant en fait
au champ de pesanteur g0
b. Manipulation
 Ouvrir le logiciel Latispro. Cliquer sur l’icône Lecteur de séquences AVI. Ouvrir le fichier TP1Schutvert.
 Revenir à la première image, puis étalonner et sélectionner comme origine la position de la balle
 Effectuer le pointage des différentes positions de la balle après avoir cliqué sur sélection manuelle des points
 Dans la fenêtre paramètre à gauche, cliquer sur liste des courbes et faire glisser Mouvement Y sur l’axe vertical
 Afin de permettre une étude plus efficace, « corriger » le pointage en modélisant cette courbe : cliquer sur l’icône
modélisation, faire glisser la courbe mouvement Y dans la courbe à modéliser, puis choisir le modèle adéquat, et cliquer
sur calculer le modèle : la courbe « corrigée » s’affiche
 La vitesse de la balle peut être calculée en dérivant la courbe suivante : dans le menu traitement, calculs spécifiques,
sélectionner Dérivée. Faire glisser la courbe Modèle de mouvement Y dans la fenêtre, et lancer le calcul. La courbe
s’affiche
c. Exploitation
1) Que peut-on dire de la courbe représentant la vitesse de la balle ?
2) A l’aide des fonctionnalités du logiciel, déterminer le coefficient directeur de cette courbe : a =
3) Que peut-on dire de cette valeur ? Commenter par rapport au texte présenté en principe
4) Calculer l’écart relatif g0 = lg0-g0thl
g0th 100