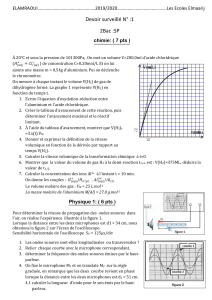
Plan Ondes Sonores dans les fluides

PSI* 1 Ondes sonores
ONDES SONORES DANS LES FLUIDES
I. Approche qualitative
A. Quelques résultats expérimentaux
 Faible atténuation
 Faible dispersion
 Quelques valeurs dans différents milieux :
Phase du milieu
Nature du milieu
Vitesse du son
(m/s)
Gazeux
Dioxyde de Carbone (CO2)
260
Gazeux
Oxygène
320
Gazeux
Air
330
Gazeux
Hélium
930
Gazeux
Hydrogène
1270
Liquide
Mercure
1450
Liquide
Eau douce
1460
Liquide
Eau de mer
1520
Solide
Acier
5000
Solide
Verre
5500
Solide
Granite
5950
Fortement fonction de la température dans les gaz (cf.infra)
 Gammes de fréquence
B. Mécanisme de la propagation
 Couplage surpression – vitesse de déplacement
 Influence de l’inertie et de la compressibilité : expression de c par analyse dimensionnelle
II. Equation d’onde
Notion de particule de fluide
Notations : P(M, t) = P0 + p(M, t) ; (M, t) ; t + µ(M, t)
A. Relation fondamentale – Approximation acoustique
  << c et a << 
p(M,t))

PSI* 2 Ondes sonores
B. Equation de conservation de la masse
(µ) = - div()
C. Hypothèse adiabatique
µ = Sp(M, t)
D. Equation de D’Alembert
 -   = 0 ; c = 
Pour un gaz supposé parfait : c = 
III. Solutions de l’équation
A. Ondes planes progressives harmoniques
 p(x, t) = p0exp(j(t – kx) ; (x,t) = v0exp(j(t – kx)
 Impédance acoustique : ZC = c
B. Ondes sphériques
C. Ondes stationnaires
 Expérience du tube de Kundt
 Une toute récente technique de lévitation : https://www.youtube.com/watch?v=odJxJRAxdFU
et https://www.youtube.com/watch?v=NLgD3EtxwdY
IV. Etude énergétique
A. Puissance échangée à travers une surface
Le vecteur densité de courant d’énergie sonore est défini par :  = p(M,t) (M, t)
B. Bilan d’énergie
 div( ) + 
, où e est la densité volumique d’énergie sonore e = ½ + ½ Sp2
 Application à l’OPPM
C. Intensité acoustique – Niveau sonore
 IS = <>
 L = 10log( IS
,0
) ; IS,0 est le seuil d’audition
minimum pour l’oreille humaine à
1 kHz : 10-12 W.m-2.

PSI* 3 Ondes sonores
V. Réflexion et réfraction d’une OPPH à l’interface entre deux fluides
A. Conditions aux limites
 Continuité de la vitesse par non-miscibilité à l’interface
 Continuité de la pression à l’interface
B. Coefficients de réflexion et de transmission en amplitude
 Forme des ondes de pression incidente, réfléchie et transmise
 Forme des ondes de vitesse incidente, réfléchie et transmise en fonction des ondes de
pression
 Expression des conditions aux limites
 =,1,2
,1+,2
; =2,1
,1+,2
=,1,2
,1+,2
; =2,2
,1 +,2
C. Coefficients de réflexion et de transmission en énergie
 Expression des normes des vecteurs de Poynting sonores moyens incident, réfléchi et
transmis.
 R = (,1,2
,1+,2
)2 et T = (2,1 ,2
,1+,2
)2
 La conservation de l’énergie impose R + T = 1
 Adaptation d’impédance si R = 0
 Importance de l’adaptation d’impédance pour l’échographie ultrasonore
Légende : 1. Sondes 2. Ecran 3. Flacon de gel 4. et 5. Consoles de commande et d’acquisition
 Importance des pavillons acoustiques : voir le TD 15