Circuit électrique en surtension

INSA de Rouen - STPI1 - E.C. P3
Circuit ´electrique en surtension
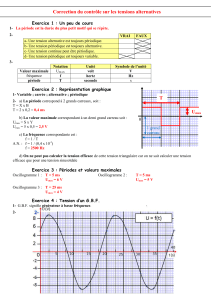
On consid`ere le circuit ci-contre aliment´e par une tension si-
nuso¨ıdale e(t) d’amplitude Emax = 3 V et de pulsation ω. On
consid`ere une bobine d’inductance Lconnue : L=7 mH
1) D´eterminer analytiquement le mod`ele ´equivalent de Th´evenin
(eT h, ZT h) du dipˆole AB vu de la r´esistance R. Faire l’analyse
dimensionnelle des r´esultats.
2) D´eterminer l’expression de la tension ucomplexe aux bornes de la r´esistance Ren fonction
de eT h, ZT h, et Rpuis en fonction de e, L, C, ω et R.
3) On donne sans d´emonstration les r´esultats suivants :
•Pulsation propre du r´eseau : ω0=1
√LC
•Soit Q=RrC
Lle facteur de surtension du r´eseau
•L’amplitude de la tension u(t) est maximum pour la pulsation : ωr=ω0
q1−1
2Q2
Les d´emonstrations ne sont pas demand´ees.
Nommer le ph´enom`ene physique mis en ´evidence.
4) L’exp´erience a permis de tracer l’amplitude Umax de la tension aux bornes de la r´esistance en
fonction de la pulsation de la f.e.m sinuso¨ıdale e(t), l’amplitude Emax de e(t) ´etant maintenue
constante. La courbe est repr´esent´ee ci-dessous.
On supposera dans toute la suite de l’exercice fr≈f0.
D´eterminer graphiquement la fr´equence de r´esonance fr.
En d´eduire la valeur de la capacit´e Cdu condensateur.
5) a) D´eterminer graphiquement la valeur de l’amplitude Ur
max de la tension u(t) `a la fr´equence
fr.
5) b) Donner la d´efinition de la bande passante `a -3 dB. Comment nomme-t-on fr´equences
d´elimitant celle-ci ? D´eterminer la largeur de la bande passante ∆fde cette r´esonance. On
exposera la m´ethode sur une reproduction de la courbe donn´ee ci-dessus.
6) a) D´eterminer l’expression analytique de Ur
max en fonction de Emax, R, L et C, puis de Q
et Emax.
6) b) D´eterminer la valeur num´erique de Q. Commenter alors l’appellation facteur de surtension
donn´ee `a Q. L’hypoth`ese fr≈f0est-elle bien justifi´ee ?
6) c) En d´eduire la valeur de la r´esistance R.
7) D´eterminer l’expression analytique de l’amplitude Ir
max du courant i(t) dans la r´esistance
Ren fonction de Emax, Q et Rpuis de Emax, L et C. Cette valeur d´epend-elle de R? R´ealiser
l’application num´erique.
1

INSA de Rouen - STPI1 - E.C. P3
Correction
1) Les ´equivalences entre les g´en´erateurs de Th´evenin et de Norton donnent les circuits ci-
dessous :
avec η=e/ZC=jCωe
Une association de dipˆoles en parall`ele donne : 1
ZT h
=jCω +1
jLω ce qui donne
ZT h =jLω
1−LCω2ou encore ZT h =1
jCω −1
Lω (1)
Enfin, eT h =ZT h ×η=jLω
1−LCω2jCω ·eet donc eT h =−LCω2 1−LCω2eou encore
eT h =Cω
Cω −1
Lω e(2)
Analyse dimensionnelle : [jLω]=[R] et 1
jCω = [R] ce qui donne donc [Cω −1 Lω ]=[R]−1
Ainsi 
1
jCω −1
Lω 
= [R]=[Z] L’expression (1) est bien homog`ene.
De mˆeme 
Cω
Cω −1
Lω 
=Z
Z[e] = [e] L’expression (2) est bien homog`ene.
2) Un pont diviseur de tension donne : u=R
ZT h +Rece qui s’´ecrit :
u=R
1
jCω −1
Lω +R
eT h et finalement u=jRCω
1 + jRCω −R
Lω e
3) L’amplitude Umax de la tension u(t) passe par un maximum pour une valeur donn´ee de la
pulsation : il s’agit d’un ph´enom`ene de r´esonance.
4) La pulsation de r´esonance correspond `a l’abscisse du maximum de la courbe repr´esentant
l’amplitude de la tension en fonction de la pulsation. Graphiquement, ωr= 4200 rad.s−1. Puisque
2

INSA de Rouen - STPI1 - E.C. P3
fr=ωr
2π, on trouve donc fr= 668 Hz
Puisque ωr≈ω0,C=1
ω2
rLce qui donne C= 8,1µF .
5 a) Ur
max correspond `a l’ordonn´ee du maximum de la courbe repr´esentant l’amplitude de la
tension en fonction de la pulsation. On trouve donc Ur
max = 41 V
5 b) La bande passante correspond `a l’ensemble des pulsations ωtelles que Umax(ω)≥Ur
max
√2.
Les fr´equences d´elimitant celle-ci sont les fr´equences de coupure.
Ici Ur
max
√2≈29 V, ce qui donne graphiquement ∆ω= 320 rad.s−1et donc ∆f= 51 Hz
6 a) L’amplitude Umax de la tension u(t) s’´ecrit : Umax =RCωEmax
s1 + R2Cω −1
Lω 2
A la r´esonance, puisque ωr≈ω0=1
√LC , on a donc Ur
max =RCωrEmax et donc Ur max =RrL
C
ce qui donne finalement Ur
max =QEmax
6 b) Q=Ur
max
Emax
=41
3et donc Q≈14
A la r´esonance, on a Ur
max =QEmax, c’est `a dire que la tension aux bornes de la r´esistance est
tr`es sup´erieure `a la tension d’alimentation du circuit, la r´esistance est donc en surtension.
Plus le facteur Qest ´elev´e, plus la surtension est importante.
r1−1
2Q2=s1−1 2·(14)2≈1 puisque Q >> 1. On v´erifie donc bien que fr≈f0.
6 c) On a R=QqL
Cce qui donne R= 412 Ω
7) On a u=Ri et donc Ir
max =Ur
max
Ret donc finalement Ir
max =QEmax
Rou encore Ir
max =EmaxrC
L,
valeur ind´ependante de R. AN : Ir
max = 102mA
3