Chapitre 7. Les lignes de transmissions

Ch.7.%Les%lignes%de%transmissions
•Une$ligne%de%transmission$est$un$ensemble$de$conducteurs$utilisé$pour$transmettre$un$signal$
d'une$source$vers$une$charge.$On$peut$classer$les$lignes$de$transmission$en$deux$grands$types$:$
les$lignes$bi<ilaires$et$les$lignes$coaxiales.
•Les$lignes$bi<ilaires$:$paires$droites$
•Lignes$bi<ilaires$:$paires$torsadées$
•Lignes$bi<ilaires$:$paires$torsadées$blindées
•Le$câble$coaxial
-$immunité$importante$au$bruit$
-$les$pertes$restent$grandes$et$dépendent$
fortement$de$la$qualité$du$diélectrique$utilisé
-$la$bande$passante$est$importantes
-$utilisé$dans$le$domaine$du$câblage$vidéo,$
informatique,$de$l'électronique$basse$fréquence,$
mais$aussi$dans$le$domaine$des$hyperfréquences$
1/5

jusqu'à$plusieurs$dizaines$de$GHz
Habituellement,les$dimensions$des$circuits$étant$très$faibles$devant$la$longueur$d'onde$des$signaux$qui
se$propagent$dans$les$câbles,$cet$aspect$ondulatoire$est$négligeable$mais,$dès$lors$qu'on$transmet$de$
l'information$sur$des$longues$distances$ou$à$des$fréquences$très$élevées,$ce$n'est$plus$le$cas$et$des$
phénomènes$de$propagation$propres$à$toute$onde$apparaissent.$
•Modélisation%d'une%ligne%de%transmissions
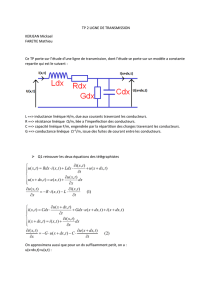
Pour$modéliser$une$ligne,$on$considère$qu'elle$est$formée$d'une$in<inité$de$tronçons$de$longueur$
in<iniment$petite$dx$en$cascade$(voir$<igure$ci-dessous).
On$dé<init$pour$la$ligne$4$grandeurs$:
On$dé<init$pour$la$ligne$:
•R-$résistance$linéique$(en$Ω.m-1)
•L-$inductance$linéique$(en$H.m-1)
•G-$conductance$linéique$(en$S.m-1)
•C-$capacité$linéique$(en$F.m-1)
Pour$les$ligne$actuelles,$la$résistance$et$la$conductance$linéique$sont$négligeables.
Le$câble$pourra$alors$être$considéré$comme$la$mise$en$cascade$d'un$grand$nombre$de$cellules$LC$
élémentaires$:
•L'impédance$caractéristique$d'une$ligne$est$dé<inie$par$:$
Zc=
√
R+jL ω
G+jC ω
.$
•Si$la$ligne$est$sans$pertes$:$
Zc=
√
L
C
•Les$paramètres$L$et$C$<ixent$également$la$valeur$de$la$célérité$des$ondes$dans$la$ligne
c=1
√
LC
2/5

•Atténuation%linéique%d'une%ligne
En$pratique,$les$pertes$font$que$l'amplitude$Usmax$de$la$tension$disponible$en$sortie$de$ligne$est$plus$
faible$que$celle$Uemax$de$la$tension$d'entrée$Uemax.$Une$ligne$de$longueur$l$(en$m)$introduit$une$
atténuation$linéique$Al$dont$l'expression$(en$dB/m)$est$:
Al=20
llog (UEmax USmax
)
•Propagation$d'un$signal$dans$une$ligne$de$transmissions
La$transmission$d'un$signal$électrique$de$fréquence$f$le$long$d'une$ligne$est$associé$à$une$onde$
électromagnétique$de$longueur$d'onde$λ.$
On$peut$modéliser$ce$signal$à$un$instant$donné$par$la$fonction$
u(x)=Asin (2⋅π⋅x
λ)
où$u(x)-est$la$tension$au$point$x,$
A-est$l'amplitude$du$signal,$
x$–$la$position$sur$la$ligne$(un$bout$de$la$ligne$est$placé$à$l'origine$de$l'axe$Ox),$$
λ-$la$longueur$d'onde$du$signal.
•Ligne%en%érgime%impulsionnel%%%:%adaptation%d'impédance%
Lorsqu'une$ligne$n'est$pas$chargée$par$son$impédance$caractéristique,$l'onde$de$tension$incidente$ui$
perçoit$la$charge$disposée$en$extrémité$de$ligne$comme$un$obstacle$sur$lequel$elle$se$ré<léchit.$Une$
onde$ré<léchie$uR$se$propageant$en$sens$inverse$(de$la$charge$vers$la$source)$prend$alors$naissance.$
Dans$ce$cas,$on$dit$que$la$ligne$n'est$pas$adaptée$et$seule$une$partie$de$la$puissance$injectée$par$le$
générateur$sur$la$ligne$est$transmise$à$la$charge,$le$reste$lui$revenant$en$retour
En$tout$point$de$la$ligne,$la$tension$est$la$résultante$des$deux$ondes$:$incidente$et$ré<léchie.$L'onde$
ré<léchie$peut$elle-même$engendrer$au$niveau$du$générateur$une$nouvelle$ré<lexion.$Pour$éviter$ce$
phénomène,$on$adapte$le$générateur$à$la$ligne$:$Rgénérateur$=$RC$.
3/5

•$le$coef<icient$de$ré<lexion$ρ$
URmax=ρUImax
Le$coef<icient$de$ré<lexion$est$lié$à$la$résistance$caractéristique$de$la$ligne$RC$et$à$la$résistance$de$
charge$par$la$relation$:
ρ=Rch−RC
Rch+RC
Ligne%en%régime%sinusoïdal%%%:%adaptation%d'impédance
Comme$en$régime$impulsionnel,$en$régime$sinusoïdal$une$ligne$est$adaptée$si$la$résistance$de$charge$
est$égale$à$la$résistance$caractéristique$Rch$=$RC
Si$la$ligne$n'est$pas$adaptée$(Rch$≠$RC$),$des$phénomènes$de$ré<lexion$ont$lieu$:$les$ondes$incidente$et$
ré<léchie$se$superposent$en$tout$point$de$la$ligne.$Il$y$a$alors$apparition$d'un$régime$d'ondes$
stationnaires.
L'amplitude$de$la$tension$varie$entre$une$valeur$maximale$UMAX$et$UMIN$.$Dans$ces$conditions$il$y$a$
dégradation$de$la$transmission$dont$la$qualité$est$quanti<iée$par$le$taux$d'ondes$stationnaires$:
TOS =UMAX
UMIN
=1+
|
ρ
|
1− | ρ |
4/5

$$
5/5