PCSI Les Ulis TD1 CI2 : SLCI - PCSI

PCSI Les Ulis
TD1
CI2
: S.L.C.I
Sciences Industrielles pour l’Ingénieur 1
Asservissement en vitesse d’une caméra mobile
Mise en situation :
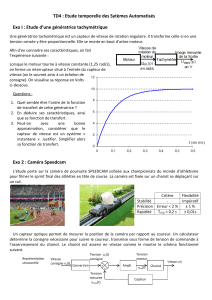
L’étude porte sur la caméra de poursuite SPEEDCAM utilisée aux derniers championnats du monde
d’athlétisme à Berlin pour filmer le sprint final des athlètes en tête de course. La caméra est fixée
sur un chariot se déplaçant sur un rail.
Un capteur optique permet de mesurer à chaque instant la position de la caméra par rapport au
coureur. Un calculateur détermine alors la vitesse réelle de l’athlète et en déduit la consigne
nécessaire à fournir à la caméra pour suivre le coureur. Cette dernière est transmise sous forme de
tension de commande à l’asservissement du chariot. Le chariot est asservi en vitesse comme le
montre le schéma fonctionnel suivant. Pour cela, un capteur de vitesse mesure en permanence la
vitesse de la caméra par rapport au sol pour pouvoir la comparer à la vitesse de consigne. Toutes les
informations provenant des capteurs sont converties en tension afin de pouvoir être traitées.
Figure 1
Partie 1 : réponse du système non asservi
On appelle S le système composé de la caméra et du chariot mobile
v(t) est la vitesse du chariot, c’est la sortie du système.
u
m
(t) est la tension du moteur, c’est l’entrée du système.
On peut donc modéliser S par le schéma bloc suivant :
position de
l’athlète
par rapport à
la caméra
Vitesse
Tension
moteur
+
-
Tension
mesurée
Tension
consigne
Calculateur Ampli. Chariot
+caméra
Capteur
de vitesse
Chariot + caméra
( )
m
u t
( )
v t

PCSI Les Ulis
TD1
CI2
: S.L.C.I
Sciences Industrielles pour l’Ingénieur 2
L’objectif de cette partie est de déterminer la réponse d’un tel système aux entrées types.
Il faut donc dans un premier temps déterminer le modèle de comportement qui permet de créer une
relation entre
( )
m
u t
et
( )
v t
.
M
: masse du système S
m
F
: force motrice de l’ensemble S, cette force est proportionnelle à la tension d’alimentation du
moteur du chariot,
. ( )
m m m
F K u t
=
r
F
: force de frottement qui s’oppose au déplacement du chariot, cette force est proportionnelle à
la vitesse du chariot,
. ( )
r
F v t
µ =
( )
m
u t
: tension d’alimentation du moteur
Questions :
Question 1 : Réaliser les diagrammes SADT A-0 et SADT A0 du système speedcam
Question 2 : En appliquant le théorème de la résultante dynamique à l’ensemble S (la somme des
forces appliquées est égale à la masse multipliée par l’accélération), démontrer que l’équation de
mouvement du chariot peut s’écrire sous la forme :
)(.)(
)(
.tuKtv
dt
tdv
m
=+ τ
Déterminer les valeurs de
τ
et de
K
en fonction des données de l’énoncé.
Pour la suite de l’étude on prendra :
0.01
s
τ
=
et
1 1
10 . .
K m s V
− −
=
Question 3 : Appliquer la transformée de Laplace à cette équation en considérant que toutes les
conditions initiales sont nulles.
Montrer que V(p) peut se mettre sous la forme
( ) ( ) ( )
m
V p H p U p
= et déterminer
H(p).
Question 4 : Modéliser le système S sous forme de schéma bloc en prenant Um(p) comme entrée et
V(p) comme sortie.
Question 5 : Déterminer la réponse impulsionnelle
( )
v t
δ
(réponse à un dirac) du système et
représentez approximativement cette réponse.
Question 6 : Déterminer la réponse indicielle
( )
u
v t
(réponse à un échelon unitaire) du système S.
Question 7 : Justifier l’allure de cette courbe à partir de la réponse impulsionnelle (figure 2)
théorique obtenue à l’aide d’un logiciel de simulation.

PCSI Les Ulis
TD1
CI2
: S.L.C.I
Sciences Industrielles pour l’Ingénieur 3
Figure 2
Question 8 : Déterminer la réponse du système à une rampe
( )
r
v t
fonction de K et de
τ
On prendra
( ) . ( )
r t t u t
=
Partie 2 : performances du système asservi
Pour améliorer les performances du système, il est nécessaire de l’asservir en vitesse selon le
schéma de principe suivant :
On extrait du cahier des charges les performances attendues de la caméra :
• Erreur statique nulle
• Temps de réponse à 5% : 0.08s
Le chariot est actionné par un moteur électrique piloté par sa tension d’entrée u
m
(t). Cette tension
est obtenue à l’aide d’un amplificateur fournissant une tension u
m
(t) proportionnelle à la tension de
commande ε(t) (le gain K
A
est réglable et peut au maximum être égal à 20). Un capteur de vitesse
mesure la vitesse v(t) et renvoi une information de tension u
e
(t) proportionnelle à la vitesse v(t)
(gain J = 0,3 V.s/m). Cette tension est ensuite comparée à la tension de consigne Uc pour former
l’écart ε(t).
Vc
V
Um
+
-
Ue
Uc
J KA H(p)
J
ε(t)

PCSI Les Ulis
TD1
CI2
: S.L.C.I
Sciences Industrielles pour l’Ingénieur 4
Question 9 : Expliciter à partir de schémas les critères de performance du cahier des charges
présentés.
Question 10 : En utilisant la formule de Black (que vous redémontrerez), calculer littéralement la
fonction de transfert
Tc
V(p)
H (p)
V (p)
= du chariot asservi.
On cherche maintenant à caractériser les performances du système asservi, c’est à dire la rapidité et
la précision.
Question 11 : En calculant la valeur à convergence de v(t) suite à une entrée en échelon
c
v (t) u(t)
=, déterminer si le système est précis (pour ce calcul on prendra Ka=1). Comment
augmenter cette précision? Est-il possible de satisfaire le cahier des charges en terme de précision.
Question 12 : Déterminer la rapidité du système. Comment augmenter la rapidité ? Quelle sera la
conséquence sur la précision ? Est-il possible de satisfaire le cahier des charges en terme de
rapidité.