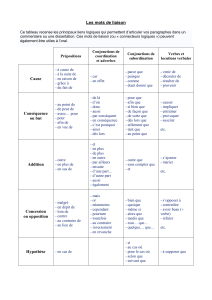
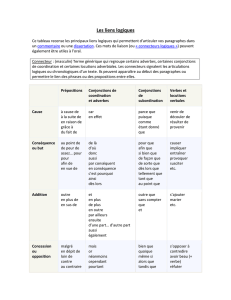
Chapitre II - Analyse et synthèse des circuits logiques combinatoires

Composants analogiques et logiques
Chapitre II - Analyse et synthèse des circuits logiques
combinatoires
II.1. Portes élémentaires :
Fig. 1 : Symboles des portes élémentaires.
Dans un boîtier de circuit intégré celui-ci peut comporter 14 broches comme celui présenté sur . On
compte sur ce boîtier
–2 bornes d'alimentation , + et masse -pin 7 et 14-,
–12 bornes disponibles pour les entrées/sorties des portes logiques.
Dans ce cas un boîtier peut contenir :
–6 inverseurs,
–4 portes à 2 entrées,
–3 portes à 3 entrées,
–2 portes à 4 entrées,
–1 portes à 8 entrées,
II.2. Fonctions logiques simples :
Les éléments que l'on retrouve le plus couramment sont les portes logiques NAND et NOR. Car
avec ces 2 types de portes ont peut réaliser l'ensemble des fonctions logiques possibles.
Fait sous Linux et OpenOffice/StarOffice page 1/4
a
b
cf
a
a
a
b
cf
a
b
cf
a
b
cf
NON ET -NAND- NON OU -NOR-
NON
ET -AND- OU -OR-

Composants analogiques et logiques
Fig. 2. Fonctions élémentaires et portes NAND.
Fig. 3. Fonctions élémentaires et portes NOR.
comment fabriquer une porte OU EXCLUSIF?
Rappel :
Fait sous Linux et OpenOffice/StarOffice page 2/4
NON ET -NAND-
a
b
a
b
a
a.b=ab
a.b=ab=ab
a.a=a
ab=a.b=a.b
b
a
NON
ET
OU
NON OU -NOR-
a
aa=a
a
b
a
b
b
a
ab=a.b
a.b=ab=ab
ab=a.b=a.b
NON
ET
OU

Composants analogiques et logiques
a b f
0 0 0
0 1 1
1 0 1
1 1 0
À partir de cette table on peut en déduire la fonction logique correspondante,
f=a.ba. b
(première forme canonique).
À partir uniquement de portes NAND :
f=f=a.ba. b=a. b .a. b=ab.ab=a. aa.ba.bb. b=a.ba.b
Fig. 4 : OU Exclusif et portes NAND.
M=a.b=ab
N=a. ab =a ab =aa.b
P=b. ab =b ab =ba.b
S= aa.b . ba.b =a.ba.b=a⊕b
Fig. 5 : OU Exclusif et portes NOR.
M=ab=a.b
N=aa.b=a. a.b =a. ab =a.b
P=ba.b=b. a.b =b. ab =a. b
S= a.b a.b =a.ba.b=a⊕b
II.3. Analyse et synthèse des circuits logiques :
Ce que l'on nomme :
–analyse : c'est l'utilisation de l'algèbre de Boole et de la table de véritè pour connaître le
Fait sous Linux et OpenOffice/StarOffice page 3/4
a
b
M
N
P
S
a
bM
N
P
S

Composants analogiques et logiques
fonctionnement du circuit.
–Synthèse :
–l'utilisation de la fonction logique, sa simplification par le tableau de Karnaugh (cad l'écriture
de la table de vérité sous forme de somme de produits ou produit de sommes). On modifie
cette expression en fonction des portes disponibles.
–Réalise le logigramme
–optimise le nombre de boîtiers.
Fait sous Linux et OpenOffice/StarOffice page 4/4