1. Ingénierie
  2. Électrotechnique

Cours Fichier - Moodle UM - Université de Montpellier

Téléchargement
Ajouter à la (aux) collection (s) Ajouter à enregistré
∗
∗
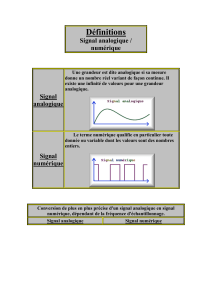
x(t)t
x[n]t
x[n] = x(nT e)
TeTe
fe=1
Te
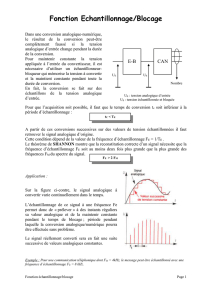
H(jω)
z
jω =2
Te
z−1
z+ 1
z H(z)
1 / 6 100%
Documents connexes
Artistes / matière numérique - Reso
Artistes / matière numérique - Reso
Signaux Analogiques et Numériques : Définitions
Signaux Analogiques et Numériques : Définitions
PANETTO Jérémy 22/02/09
PANETTO Jérémy 22/02/09
conversion analogique numerique
conversion analogique numerique
4AO/8AI-3 Module 4 Sorties analogiques 12 bits et 8 Entrées
4AO/8AI-3 Module 4 Sorties analogiques 12 bits et 8 Entrées
4AO/8AI-1 Module 4 Sorties analogiques 8 bits et 8 Entrées
4AO/8AI-1 Module 4 Sorties analogiques 8 bits et 8 Entrées
LE SON NUMERIQUE
LE SON NUMERIQUE
La numérisation du son - E
La numérisation du son - E
Chapitre 20 : De la chaine de transmission de l`information à la
Chapitre 20 : De la chaine de transmission de l`information à la
Fonction Echantillonnage/Blocage
Fonction Echantillonnage/Blocage
La catégorie de ce document est-elle correcte?
  1. Ingénierie
  2. Électrotechnique
Merci pour votre participation!

Faire une suggestion

Avez-vous trouvé des erreurs dans l'interface ou les textes ? Ou savez-vous comment améliorer l'interface utilisateur de StudyLib ? N'hésitez pas à envoyer vos suggestions. C'est très important pour nous!

Produits
Assistance
© 2013 - 2025 studylibfr.com toutes les autres marques déposées et droits dauteur sont la propriété de leurs propriétaires respectifs
GDPR Confidentialité Conditions d'utilisation