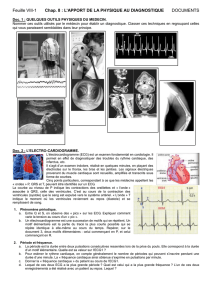
Ondes électromagnétiques et rayons lumineux (1) Le principe de

Ondes électromagnétiques et rayons lumineux (1)
Limites de l’optique géométrique :
Pour un faisceau réel les lignes de champ du vecteur de Poynting
ne sont pas rectilignes mais courbes.
Les seules zones où l’on peut faire un lien entre la propagation de l’énergie et
Les rayons lumineux sont les zones où l’onde a la structure d’onde quasiment plane
pour la phase et l’amplitude.
Dans ce cas le vecteur de Poynting est orthogonal aux surfaces d’ondes et ses
lignes peuvent être assimilées aux rayons lumineux.
Le principe de Huygens pour expliquer la propagation
d’un front d’onde.

Ondes électromagnétiques et rayons lumineux (2)
Principe de Huygens : Tout point d’un front d’onde primaire sert de source
à des ondes sphériques secondaires telles que le front d’onde plus tard est
l’enveloppe de ces ondes. De plus, ces ondes avancent avec une longueur
d’onde et une fréquence égale à celle de l’onde primaire.
rayons lumineux
Onde plane Onde sphérique

Ondes électromagnétiques et rayons lumineux (3)
Propagation d’une surface d’onde
Soit un champ électrique noté :
!
" r,t
( )
=E0r
( )
ei
# r,t
( )
# r,t
( )
= $ r
( )
% & t
à l’instant t en r0 :
À l’instant t+ τ en r0 +dr :
!
" r
0,t
( )
= # r
0
( )
$ % t= "
0
!
" r0+dr,t+ #
( )
= $ r0+dr
( )
% & t+ #
( )
= $ r0
( )
+grad $ .dr % & t+ #
( )
!
" r0+dr,t+ #
( )
= " r0,t
( )
= "
0si grad
$ .dr = %#
ou encore
k r0
( )
k r0
( )
.dr =
%
k r0
( )
# =v #

Ondes électromagnétiques et rayons lumineux (4)
Conclusions :
- La notion de rayon lumineux est liée à la notion de front d’onde
(ou surface d’onde)
- Un rayon lumineux ne peut se concevoir seul --> On parle d’une famille de
rayons lumineux. Elle définit des fronts d’ondes qui sont des surfaces
orthogonales à ses rayons.
- Réciproquement un front d’onde détermine localement les rayons, ce sont
des courbes qui lui sont orthogonales.

Ondes électromagnétiques et rayons lumineux (5)
Chemin optique : loptique = n1 AB + n2 BC + n3 CD
!
Tp=AB
v1
+BC
v2
+CD
v3
=AB
c
n1
+BC
c
n2
+CD
c
n3
=1
cn1AB +n2BC +n3CD
[ ]
=1
cloptique ABCD
( )
!
" #
AD =
$
cloptique ABCD
( )