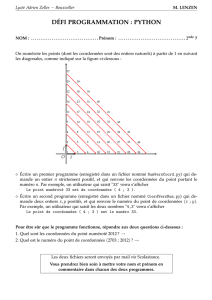
Prise en main Sympy

Prise en main du module complémentaire
Sympy de calcul formel pour Python
Ce module sous Python n'ayant pas l'ergonomie d'autres logiciels uniquement dédiés au calcul
formel, il n'est pas à recommander pour une étude demandant une succession de calculs.
Il permet cependant d'accéder à des calculs formels élémentaires et peut par exemple être
utilisé pour calculer une fonction dérivée, une primitive …
Il ouvre également de nouvelles possibilités dans la programmation d'algorithme sous Python.
On pourrait imaginer une étude d'une suite de nombres dérivés ou d'intégrales …
Vous trouverez toutes les informations pour le téléchargement du module et une explication
complète des possibilités de ce module à l'adresse suivante : http://sympy.org/index.html
Pour toutes les instructions en Python il faut impérativement respecter les majuscules et les
minuscules.
Pour faire appel à ce module, il faut saisir : from sympy import *
Voici quelques possibilités offerte par ce module.
Différents nombres.
1 désigne le nombre entier. Ainsi 1/4 donne 0 qui est l'arrondi à l'unité du quotient.
1.0 désigne le nombre réel. Ainsi 1/4 donne 0.25.
Rational(3/2) désigne le nombre rationnel
Error!
.
Le nombre  s'écrit pi, le nombre i s'écrit I, le nombre e s'écrit e, l'infini s'écrit oo (soit deux
fois la lettre "o").
Les variables utilisées doivent être déclarées. Par exemple : x=Symbol('x')
Ainsi si on saisit : >>> 3*x + 2 + x
On obtient : >>> 2 + 4*x
Opérations.
Développer. Si on saisit : >>> ((x+y)**2).expand()
On obtient : >>> 2*x*y + x**2 + y**2
Substituer. Si on saisit : >>> (2*x + x**3).subs(x,2)
On obtient : >>> 12
Réduire au même dénominateur : Si on saisit : >>> together(1/x + 1/y)
On obtient : >>> (x + y) / (x*y)
Calculer des limites : Si on saisit : >>> limit(1/x,x,oo)
On obtient : >>> 0
Dériver : Si on saisit : >>> diff(1/x,x)
On obtient : >>> -1/x**2
Intégrer : Si on saisit : >>> integrate(sin(x) , (x,0,pi/2))
On obtient : >>> 1
Résoudre des équations.
Pour résoudre l'équation x4 – 1 = 0 Saisir : >>> solve(x**4-1,x)
On obtient : >>> [1, -1, -I, I]