STATISTIQUES : AJUSTEMENT D`UN NUAGE DE POINTS

STATISTIQUES : AJUSTEMENT AFFINE D’UN NUAGE DE POINTS
Objectif : un nuage de point étant donné (par exemple série chronologique), on souhaite le modéliser par
une courbe (par exemple pour la prolonger pour faire des prévisions ).
On parle alors de courbe d’ajustement.
On s’occupe ici du cas où les points sont à peu près alignés : on va donc faire un ajustement affine.
On peut procéder : - au jugé
- par la méthode de Mayer
- par la méthode des moindres carrés
On note G le point moyen du nuage :
son abscisse est la moyenne des abscisses des points du nuage,
son ordonnée est la moyenne des ordonnées des points du nuage
Propriété : les droites d'ajustement obtenues par la méthode de Mayer ou par la méthode des
moindre carrés passent par le point moyen G
1. la méthode des points moyens : la droite de Mayer
On partage le nuage en deux sous-nuages.
On calcule le point moyen de chaque sous-nuage : on obtient deux points G1 et G2.
La droite (G1G2) est une droite d’ajustement du nuage.
2. la méthode des moindres carrés : la droite de « régression linéaire »
a) comment calculer l'équation de cette droite
On peut déterminer l'équation par la formule du manuel (page 148),
mais en pratique on utilise la calculatrice:
STAT → EDIT → compléter L1 avec les valeurs de x et L2 avec les valeur de y correspondantes
STAT → CALC → LINREG(ax+b) → ENTER
la calculatrice affiche les valeurs a et b de l'équation y=ax+b
b) intérêt de cette droite
Propriété (admise): la droite de « régression linéaire » est la droite « la plus proche » du nuage.
On cherche la droite « la plus proche « du nuage
Il faut pour cela mesurer, pour chaque droite possible, la distance qui la sépare du nuage.
On choisit de mesurer cette distance de la façon suivante :
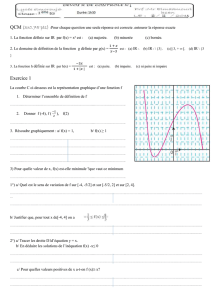
Soit (d) une droite.
Pour chaque point Mi du nuage, de
coordonnées (xi ; yi), on place le point Pi
d’abscisse xi appartenant à la droite (d) :
Pi (xi ; y’i).
On calcule alors les écarts Di entre Mi et
Pi : Di = /y’i – yi/
La « distance » qui sépare (d) du nuage est
alors :
D = la somme des carrés de ces écarts
D = D1² + D2² + D3² + D4²

Cette méthode de calcul des carrés pour en minimiser la somme s'appelle méthode des moindres carrés
la propriété affirme qu'il existe une droite qui minimise cette distance : c'est la droite de « régression
linéaire ».
c) comment tracer cette droite ?
rappel : pour tracer une droite d'équation donnée, on en cherche des points ; Pour cela on choisit des valeurs
de x et on calcule les y correspondants.
rappel : la droite de « régression linéaire » passe par le point moyen G, cette propriété permet de vérifier
que notre droite est correcte