chap-4-l-oeil-et-la

Chapitre 4 L’œil et la loupe
I- L’œil :
1) Description de l’organe ‘œil’:
Notre œil est un récepteur de lumière. Du point de vue optique, il est constitué essentiellement :
 de la pupille par laquelle entre la lumière (son diamètre est variable)
 du cristallin, qui concentre le flux de lumière pour former l’image sur la rétine
 de la rétine, surface sensible qui transforme l’énergie lumineuse en signal électrique.
Ce signal électrique est transmis par le nerf optique à certaines zones du cerveau, qui l’interprètent.
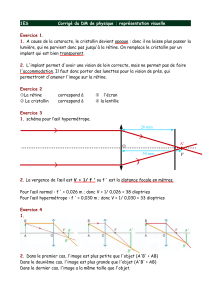
2) Modèle de l’œil :
Pour un physicien un œil peut être modélisé par les trois éléments suivants :
 un diaphragme dont le diamètre peut varier selon la luminosité de l’objet
 une lentille convergente de distance focale pouvant varier selon la distance à laquelle se situe l’objet :
voir 3) pour l’explication
 un écran sur lequel se forme l’image de l’objet. lentille convergente
(cristallin)
Schéma du modèle de l’œil : diaphragme écran (rétine)
(pupille)
Le diaphragme joue le rôle de la pupille, la lentille convergente joue le rôle du cristallin et l’écran joue le
rôle de la rétine…
3) Pourquoi dit-on que l’œil est un système optique convergent à distance focale variable ?
Un objet n’est vu nettement par l’œil que si son image se forme sur la rétine située à une distance fixe du
cristallin.
Problème : Comment se fait-il que notre œil (du moins si il n’est pas malade : myopie,…) nous permette
d’observer nettement des objets à des distances très différentes de nous?
En effet, sur le banc d’optique nous avons eu l’occasion d’observer qu’à une position de l’objet et de la
lentille donnée, il ne correspond qu’une position de l’écran pour avoir une image nette…Si on change la
distance entre l’objet et la lentille, il faut changer la position de l’écran.

Dans le cas de l’œil, quand on change la distance de l’objet qu’on regarde (une montagne au loin ou un livre
tout près), la distance lentille-écran (cristallin-rétine) reste évidemment la même mais c’est la distance
focale du cristallin qui change comme nous allons le voir. C’est l’accommodation.
 Le cristallin au repos est fait pour observer des objets à l’infini car son foyer image F’ est alors sur la
rétine : (rappel : les rayons issus du même point d’un objet à l’infini sont parallèles)
 Si on observait un objet beaucoup plus proche sans rien changer, on serait alors dans la situation
suivante et l’image serait floue sur la rétine (car elle se formerait loin derrière…) :
 Mais en fait l’œil réagit spontanément sans qu’on s’en rende compte : des muscles compriment le
cristallin afin de diminuer sa distance focale en le rendant plus ‘bombé’ : on dit que l’œil
accommode. Le système ‘œil’ est alors plus convergent et on est dans la situation suivante où
l’image est à nouveau nette sur l’écran :
 Si on observe un objet encore plus proche de l’œil, les muscles doivent appuyer encore plus sur le
cristallin…mais il y a une limite : si l’objet est à moins de 25 cm de l’œil, le cristallin est à la limite
de sa déformation possible (au-delà l’œil se fatigue très vite : essayez, ça fait mal…).
C’est le fameux dm (distance minimale de vision distincte) qui vaut environ 25 cm.
Remarque : comme le suggère les schémas ci-dessus, l’image formée sur la rétine est renversée par rapport à
l’objet…et c’est en fait le cerveau qui la remet à l’endroit !
Conclusion :
L’œil est un système optique à distance focale variable (grâce à son cristallin déformable).
Quand on observe un objet ‘à l’infini’, l’œil n’accommode pas et ne se fatigue donc pas.
Il est possible d’observer un objet proche jusqu’à 25 cm mais il faut accommoder ce qui peut fatiguer
à la longue. Evidemment, plus l’objet est proche, plus il faut accommoder et plus c’est fatiguant.
La distance minimale à laquelle on peut observer un objet distinctement et sans fatigue excessive
s’appelle la distance minimale de vision distincte. Elle dépend de l’âge et des défauts de l’œil. Elle est
estimée à 25 cm pour un adulte jeune dont l’œil est normal.

4) Notion de diamètre apparent :
L’idée qu’un observateur se fait de la taille de l’objet qu’il observe dépend non seulement de la taille réelle
de l’objet mais aussi de la distance à laquelle il se trouve de l’observateur.
- Définition :
On appelle diamètre apparent d’un objet l’angle sous lequel cet objet est vu.
Si on note AB la taille de l’objet et d la distance qui le sépare de l’œil de l’observateur, le diamètre
apparent  est défini par :
Quand AB<<d, l’approximation tan des petits angles permet d’écrire
d
AB
. L’angle est alors
nécessairement exprimé en radians (AB et d étant exprimées avec la même unité, le mètre par exemple).
- Limite de l’œil :
On admet généralement que l’angle minimal sous lequel on peut observer 2 points à l’œil nu tout en les
distinguant est d’environ 3.10-4 radian. Si l’angle est plus petit, l’œil ne distingue plus qu’un seul point…
Ainsi une loupe est un instrument d’observation utilisée pour donner d’un objet (ou d’une partie d’un objet)
de petite taille, une image de diamètre apparent plus grand que lorsqu’on observe l’objet à l’œil nu.
II- L’observation à travers une loupe :
1) Modélisation d’une loupe :
On peut modéliser une loupe par une lentille convergente de distance focale f ’ de l’ordre de quelques cm.
L’objet est situé entre la lentille et le plan focal objet.
L’image se forme donc avant la lentille. Elle est dans le même sens que l’objet et plus grande que lui.
C’est cette image que l’œil observe. Elle lui sert d’objet dont il forme l’image sur la rétine.
Schéma n°1:
2) Grossissement de la loupe:
 La loupe étant un instrument d’observation, la façon dont elle modifie cette observation est décrite en
optique en comparant le diamètre apparent de l’objet observé à l’œil nu et le diamètre apparent
'
de
l’objet observé à la loupe.
 Le grossissement G est défini par la relation : G =
'
G étant sans unité, et
'
étant exprimés en radians et suffisamment petits pour que l’approximation tan 
  soit acceptable.
tan
d
AB
Schéma :

La valeur de G dépend de la loupe et des façons dont on observe l’objet à l’œil nu et à travers l’instrument.
Cependant, pour attribuer une valeur qui permette d’apprécier les performances d’une loupe et de les
comparer entre elles, les opticiens ont précisé des conditions particulières d’observation auxquelles ils ont
associé la notion de grossissement commercial.
 Le grossissement commercial :
Le grossissement commercial GC est défini pour les deux conditions d’observation particulières suivantes :
 Observé à l’œil nu, l’objet est situé à la distance minimale de vision distincte dm.
Dans ces conditions
m
d
AB
.
Explication sur ce choix : c’est naturel ! Si on veut comparer les performances de la loupe à celle de l’œil
nu, autant comparer à l’œil nu utilisé dans la situation où il est le plus performant pour voir les
détails…c’est-à-dire en s’approchant à 25 cm de l’objet à observer !
 Observé à travers l’instrument, il est placé dans le plan focal objet de la lentille qui le modélise.
Schéma n°2:
Dans ces conditions,
'
=
'f
AB
D’où GC =
m
d
AB
f
AB
'
=
'f
dm
.
Explication sur ce choix :
- On peut très bien utiliser une loupe sans mettre obligatoirement l’objet dans le plan focal de la loupe. Voir
le schéma n°1.
L’image de l’objet est à distance finie (il faut impérativement que cette distance soit supérieure à dm sinon
l’œil sera incapable d’accommoder) : l’œil accommode alors de façon à avoir une image nette sur la rétine.
La valeur du grossissement d’une loupe dépend alors de l’endroit ou l’on place l’objet entre F et O (centre
optique de la loupe).
- Mais il est plus judicieux de placer l’objet observé exactement en F car alors son image est renvoyée à
l’infini à gauche de la lentille et c’est comme si l’œil observait un objet à l’infini : les rayons issus d’un
point de l’objet sont parallèles entre eux après avoir traversé la loupe. L’œil reçoit ces rayons parallèles
entre eux et n’a pas besoin d’accommoder pour en faire une image nette sur la rétine. C’est la situation la
plus reposante pour l’œil et c’est d’ailleurs celle qu’on adopte spontanément sans s’en rendre compte
quand on utilise une loupe…
C’est pour cela que c’est dans cette situation qu’on défini le grossissement ‘commercial’ (ou grossissement
‘standard’ d’une loupe : GC.
Conclusion sur la loupe :
Une loupe a un double intérêt :
- elle permet d’augmenter la diamètre apparent sous lequel est vu un objet (on voit donc plus
de détails)
- elle permet à l’œil d’observer une image de l’objet renvoyée à l’infini par la loupe donc dans
les conditions les plus reposantes pour lui : pas besoin d’accommoder au maximum en se
rapprochant autant que possible de l’objet à observer !