VI. Le télescope de Newton.

Terminale S Spécialité TP de physique
Objectifs
Le but de ce TP est de modéliser une lunette astronomique et un télescope de Newton.
I. Problème posé :
Une lunette astronomique permet de voir une image grossie d’un objet éloigné.
Vous devez simuler une lunette astronomique sur le banc optique en utilisant les deux lentilles à votre disposition et sachant que :
Dans une lunette astronomique, on regarde à la loupe (l’oculaire), l’image formée par une lentille
convergente (l’objectif), d’un objet éloigné.
 Rappeler les conditions d’observation sans fatigue pour l’œil.
 Quelle est celle des deux lentilles qui permet d’obtenir l’image intermédiaire la plus grande ? En déduire quelle est la
lentille qui sera utilisée en objectif.
 Positionner sur le banc optique L1 et L2 de sorte que l’on puisse distinguer les graduations de la règle placée à 4 ou 5 m de
l’objectif.
II. Construction à l’échelle :
Représenter le schéma correspondant au montage réalisé. Prendre l’échelle 1/5 sur l’axe optique.
Corriger votre construction à l’aide du logiciel « simulation d’un banc d’optique ».
Vérifier les éléments de la construction par le calcul en complétant le tableau suivant :
L1 : objectif
L2 : oculaire
Objet : AB
Image A’B’
Objet : A’B’
Image A’’B’’
Position
Formule de
conjugaison à
utiliser
Grandeurs
algébriques de
position
Caractéristiques
Soit  est l’angle sous lequel on voit l’objet situé à l'infini sans instrument.
5. La lunette astronomique et le
télescope.

Soit ’ est l’angle sous lequel on voit l’objet à travers l’instrument.
Le grossissement de la lunette est donné par la relation : G = ’ / .
Exprimer puis calculer le grossissement de la lunette simulée.
Etudier la documentation sur les lunettes astronomiques fournie au TP 1.
Discuter la qualité d’une lunette astronomique.
Remarque : L’image finale obtenue grâce à la lunette d’un objet situé à l’infini est elle aussi à l’infini : cette lunette est un système
optique afocal.
V. Position de l’œil : le cercle oculaire.
Repérer le cercle oculaire.
Noter sa position et son diamètre.
Retrouver les caractéristiques du C.O. (cercle oculaire) sur un schéma à la même échelle qu’au II.
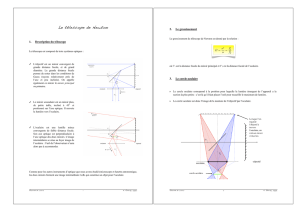
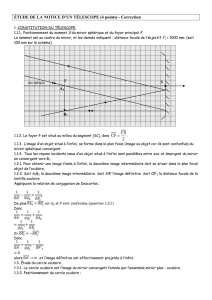
VI. Le télescope de Newton.
Tout comme pour la lunette astronomique il s’agit d’observer à la loupe l’image d’un objet éloigné,
l’objectif étant un miroir sphérique.
A l’aide de la documentation fournie au TP 1, proposer un schéma permettant de modéliser expérimentalement le télescope de
Newton.
Déterminer la distance focale du miroir dont vous disposez.
Réaliser à l’aide du matériel dont vous disposez ce télescope afin d’obtenir une image des immeubles sur Van Horne.
On utilisera une lentille + 4 comme oculaire.
Calculer le grossissement théorique de ce télescope.
Remarque : Le grossissement d’un télescope a la même formule que celui d’une lunette astronomique. C’est aussi un système
optique afocal.
Construire sur un schéma à l’échelle le trajet de la lumière dans un télescope de Newton dont l’objectif et l’oculaire ont une
distance focale, respectivement de 220 cm et 13 cm
L’échelle utilisée sera 1/10 sur les axes optiques.
VI. Pourquoi l’astronome amateur préfère-t-il le télescope à la lunette ?
Utiliser la documentation fournie au TP 1 pour répondre à cette question.

I. Problème posé :
 Rappeler les conditions d’observation sans fatigue pour l’œil.
L’image finale A’’B’’ devra se trouver à l’infini.
Cela suppose que l’image intermédiaire A’B’ se trouve dans le plan focal objet de L2.
 Quelle est celle des deux lentilles qui permet d’obtenir l’image intermédiaire la plus grande ? En déduire quelle lentille sera
utilisée en objectif.
Les élèves disposent de deux lentilles :
ils doivent déterminer expérimentalement la distance focale de chaque lentille (méthode de l’objet à l’infini : fin TP 1).
Objectif : L1 : distance focale 25 cm. (+4)
Oculaire : L2 : distance focale 12,5 cm. (+8)
Ils pourront dessiner :
L’image d’un objet éloigné, se forme dans le plan focal image de la lentille.
L’image obtenue est d’autant plus grande que la distance focale est grande.
Ils pourront conclure que la lentille de grande distance focale sera utilisée en objectif.
Quand à l’oculaire, nous avons vu au TP 2, qu’il grossit d’autant plus que sa distance focale est petite !
 Positionner sur le banc optique L1 et L2 de sorte que l’on puisse distinguer les différentes graduations de la règle placée à 4
ou 5 m de l’objectif.
Faire travailler les élèves sur les bancs posés sur les paillasse situées à gauche (par exemple) de la salle (coté opposé aux
fenêtres pour être dans la pénombre et obtenir un bon contraste)
Placer alors les règles sur les paillasses de droite, le plus loin possible du banc, à plus de 3,5 m si possible.
Eclairer fortement la règle.
Placer L1 sur le banc et récupérer l’image intermédiaire A’B’ sur un écran.
Utiliser L2 comme loupe. Eloigner progressivement L2 de A’B’ pour observer une image nette.
II. Construction à l’échelle :
Construire la situation expérimentale à l’échelle (1/5 sur l'axe optique):
5. La lunette astronomique et le
télescope.
Corrigé

Au programme officiel figure « retrouver par construction les caractéristiques d’un objet connaissant son image ».
Aussi la construction graphique devra se faire dans l’ordre suivant :
A’’B’’ à l’infini (les rayons émergeants de la lunette sont parallèles).
Par construction, retrouver les caractéristiques de A’B’ (A’ est sur F2) .
L’objet AB étant à l’infini, A’B’ est sur F’1..
On en déduit que F’1 est confondu avec F2.
Ainsi la distance séparant les deux lentilles est égale à la somme des distances focales de l’objectif et de l’oculaire.
Une lunette utilisée dans ces conditions est dite afocale.
Vérifier les éléments de la construction par le calcul en complétant le tableau suivant dans le même ordre que la construction.
L1 : objectif
L2 : oculaire
Objet : AB
Image A’B’
Objet : A’B’
Image A’’B’’
Position
L’objet AB est à
l’infini
A’ sur F’1
A’ sur F2
A l’infini pour une
observation sans
fatigue pour l’œil.
Formule de
conjugaison à utiliser
1111 '
11
'
1
FOAOAO 
2222 '
1
'
1
''
1
FOAOAO 
Grandeurs
algébriques de
position
AO1
= - 
'
1AO
11 'FO
'
1AO
= 25 cm
'
2AO
22 FO
'
2AO
= -12.5 cm
''
2AO
= 
Caractéristiques
A l’endroit
A l’envers
Plus grosse que A’B’
A l’envers
Soit  est l’angle sous lequel on voit l’objet situé à l'infini sans instrument.
Pour  petit, on peut écrire tan   = A’B’/ O1F’1.
Soit ’ est l’angle sous lequel on voit l’objet à travers l’instrument : Voir schéma ci-dessus.
Pour ’ petit, on peut écrire tan’  ’ = A’B’/ O2F2.
Le grossissement G = ’ /  de cette lunette est donné par la relation :
G =
22
11 ''
FO FO
=
1
2
V
V
= f’1/f’2
Nous avons construit une lunette de grossissement G = 8/4 = 2.
Une lunette grossit d’autant plus que la focale de l’oculaire est petite. Nous l’avons déjà vu.
Elle grossit d’autant plus que la focale de l’objectif est grande. Mais augmenter O1F’1 présente deux inconvénients :
cela augmente la longueur de l’instrument,
à trop augmenter la distance focale de l’objectif, on perd en luminosité.
F’1 = F2

C’est d’ailleurs pour cette raison qu’une autre grandeur entre en jeu : le diamètre de l’objectif ; plus il sera grand, plus lumineuse
sera l’image finale.
Ainsi une lunette portant les nombres (40070) indique un grossissement G = 400.
70 correspond au diamètre de l’objectif en mm
V. Position de l’œil : le cercle oculaire.
Orienter la lampe face à la lunette simulée. La lampe doit être placée le plus loin possible.
Déplacer l’écran après L2 et repérer la section du faisceau la plus étroite sortant de la lunette.
Rappeler que le C.O. est l’image de l’objectif donnée par l’oculaire.
L’œil doit être placé à son voisinage pour recevoir un maximum de lumière.
VI. Le télescope de Newton.
Le but de cette partie sera de réaliser un télescope simulé sur la paillasse professeur, l’objet étant une feuille, sur laquelle on
place de petits points très rapprochés, placée sur le mur au fond de la salle. Les points ne doivent pas être visibles à l’œil, le
télescope va permettre de les « séparer ».
(C’est une simulation de l’observation de deux étoiles proches non visibles à l’œil. Le télescope va permettre de les distinguer
car il augmente le pouvoir séparateur.)
L’image A’B’ d’un objet situé à l’infini donnée par un miroir sphérique se trouve dans le plan focal du miroir.
Former l’image de la mire, donnée par le miroir sphérique, sur un écran (papier calque)
Pour observer cette image à la loupe, il faudrait placer l’observateur entre l’objet et l’image intermédiaire. L’observateur stoppe
alors la lumière émise par l’objet.
Discuter avec la classe des solutions possibles.
Dans le cas du télescope de Newton on place un second miroir, plan, incliné de 45 ° sur l’axe optique.
Il se forme alors une image A’ que l’on place au foyer de l’oculaire pour une observation sans fatigue pour l’œil.
Construire sur un schéma à l’échelle le trajet de la lumière dans un télescope de Newton dont l’objectif et l’oculaire ont une
distance focale, respectivement de 220 cm et 13 cm
L’échelle utilisée sera 1/10 sur les axes optiques.