Les interactions fondamentales prof

Page 1/6 17/04/2017
1 S
LES INTERACTIONS FONDAMENTALES
P 2
Objectifs :
 Savoir que toute charge électrique est multiple d'une charge élémentaire.
 Connaître l'ordre de grandeur du rapport des masses du nucléon et de l'électron.
 Connaître l'ordre de grandeur du rayon d'un atome et d'un noyau.
 Connaître et savoir appliquer la loi de Coulomb
 Savoir que dans un métal une fraction des électrons est libre de se déplacer dans tout l’échantillon, alors que
dans un isolant les déplacements des charges sont inférieurs à la taille atomique
 Savoir qu’au niveau du noyau s’exercent deux types d’interactions dont les effets sont opposés
 Savoir que la cohésion de la matière est assurée par :
- l’interaction gravitationnelle à l’échelle astronomique
- l’interaction électromagnétique à l’échelle des atomes, des molécules et de la matière à notre échelle
- l’interaction forte à l’échelle du noyau.
1.Les particules élémentaires
Dans l’Univers, la matière se présente sous des formes très diverses (noyaux, atomes, molécules, ions,
phases condensées ou gazeuses, organismes vivants, systèmes astronomiques…). Elle résulte de
l’arrangement de trois particules élémentaires de bases : l’électron, le proton et le neutron.
(Les protons et les neutrons sont constitués chacun de 3 quarks mais seront considérés au lycée comme des
particules élémentaires.)
1.1.Les particules élémentaires
Historique :
Electron
De 1858 à 1897, étude des « rayons cathodiques » :
En 1879, W. Crookes constate que les rayons cathodiques sont
déviés par un aimant ;
En 1891, G. Stoney émet l’hypothèse de l’existence d’une
particule (qu’il nomme « électron ») dans les rayons
cathodiques ;
En 1895, J. Perrin montre que les rayons cathodiques sont
constitués de particules chargées négativement ;
En 1897, J. J. Thomson mesure le rapport
m
e
par action
combinée d’une force électrique et d’une force magnétique
puis fait l’identification d’un seul type de particule comme
constituant des « rayons cathodiques ») ;
En 1911, R. Millikan mesure la charge de l’électron.
Proton et neutron
En 1911, E. Rutherford met en évidence l’existence de noyaux
atomiques chargés positivement.
En 1914, E. Rutherford suggère l’existence du proton
En 1919, E. Rutherford réalise une « transmutation nucléaire »
en bombardant des noyaux d’azote par des particules , il
obtint un autre élément et une particule positive nommé
« rayon H » puis proton.
En 1920, E. Rutherford émet l’hypothèse de la présence de
neutrons dans le noyau.
En 1932, J. Chadwick met expérimentalement en évidence
l’existence des neutrons.
 L’électron est une particule élémentaire de masse
e
m
et de charge électrique négative
e
qe
où e est
la charge élémentaire.
 Le proton est une particule de masse
p
m
et de charge électrique positive
p
qe
.
 Le neutron est une particule de masse
n
m
et de charge électrique nulle. La masse du neutron est
proche de celle du proton.
Masse
Charge
Le coulomb, de symbole C,
est l'unité de charge électrique
dans le système international
(S.I.).
Électron
kg109,1m 13
e
C101,6q 19
e
Proton
27 27
p
m 1,6726231 10 kg 1,67 10 kg
C101,6q 19
p
neutron
27 27
n
m 1,674929 10 kg 1,67 10 kg
0qn
La charge élémentaire :
L'électron porte la plus petite charge électrique existante dans l'état actuel de nos connaissances. On la
considère comme indivisible et on l'appelle charge élémentaire.
Une charge électrique est toujours un multiple de la valeur de la charge élémentaire notée
C101,6e 19
.

Page 2/6 17/04/2017
Comparaison des masses d'un nucléon et d'un électron :
27 33
31
p
e
1,67 10 1,8 10 2 10
9,1 1
m
m0
La masse d'un nucléon est 2 000 fois supérieure à celle d'un électron.
1.2. L'atome et le noyau
Dans un atome, les protons et les neutrons sont localisés dans le noyau, les électrons sont en mouvement
autour du noyau.
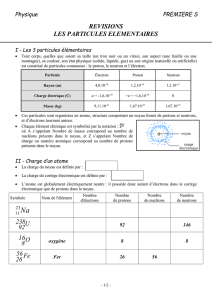
Les protons et les neutrons sont appelés les nucléons.
Le noyau d'un atome de symbole X est représenté par
X
A
Z
avec :
A le nombre de nucléons
Z le nombre de charge ou numéro atomique correspondant au nombre de protons
N = A – Z le nombre de neutrons
L'atome est électriquement neutre.
Le diamètre d'un atome est de l'ordre de
m10 10
, celui du noyau est de l'ordre de
m10 15
. (Cent mille fois
plus petit que l'atome, comparaison noyau tête d'épingle au centre du terrain de foot représentant l'atome.)
On appelle élément chimique l'ensemble des particules caractérisées par le même numéro atomique Z.
On appelle isotope les éléments chimiques dont les noyaux ont le même nombre de protons mais des
nombres de neutrons différents (Z est le même mais A est différent,
C
12
6
;
C
13
6
;
C
14
6
).
La masse d'un atome est pratiquement égale à la masse de son noyau.
atome p n e p n nucléon
m Z m (A Z) m Z m Z m (A Z) m A m     
.
Applications :
1°/ Le rayon d’un atome d’or est 0,144 nm. Le symbole de l’unique isotope de l’or est
197
79 Au
.
1.1. Quelle est la masse approchée de l’atome d’or ?
atome nucléon
m A m
A.N. :
27 25
atome
m 197 1,67 10 3,29 10 kg
1.2. Quelle est la masse volumique de l’atome d’or ?
atome
atome atome
m (Au)
(Au) V (Au)
et
3
atome Au
4
V (Au) R
3
donc
atome atome
atome 3
3Au
Au
m (Au) 3m (Au)
(Au) 44R
R
3
A.N. :
25 43
atome 93
3 3,29 10
(Au) 2,63 10 kg.m
4 (0,144 10 )
(
29 3
atome
V (Au) 1,25 10 m
))
1.3.. Comparer cette valeur avec la masse volumique de l’eau.
2
HO
Au
26,3
La masse volumique de l’or est 26,3 fois plus grande que celle de l’eau, l’or est plus dense
que l’eau.
Remarque : la masse volumique calculée n’est pas correcte car les atomes étant assimilé à des sphères, elles
ne sont pas jointives, il y a des espaces vides entre chaque atome dont nous n’avons pas tenu compte. La
masse volumique réelle est plu faible que celle calculée.
1.4. Calculer la valeur de la charge portée par le noyau de l’atome.
noyau p
q Z q Z e
A.N. :
19 17
noyau
q 79 1,6 10 1,26 10 C
2°/ Le noyau d’un atome porte une charge de
17
q 1,47 10 C
.
2.1. Calculer le nombre de charges élémentaires qu’il contient. En déduire son numéro atomique Z.

Page 3/6 17/04/2017
noyau
noyau p
q
q Z q Z e Z e
A.N. :
17
19
1,47 10
Z 92
1,6 10
2.2. Quel est le nom de cet atome ?
Uranium
2.3. Sachant que le nombre de nucléons est 238
2.3.1. Donner la composition du noyau de cet atome ;
Z 92
donc le noyau contient 92 protons.
A 238
donc
N A Z 238 92 146    
, il y a 146 neutrons.
2.3.2. Calculer la masse de cet atome en négligeant la masse des électrons ;
atome nucléon
m A m
A.N. :
27 25
atome
m 238 1,67 10 3,97 10 kg
2.3.3. Calculer la masse d’une mole de cet atome.
C’est la masse molaire de cet atome.
A atome
M(U) N m
A.N. :
23 25 1
M(U) 6,02 10 3,97 10 2,39 10 kg
soit 239 g
2. Les interactions fondamentales
2.1. Qu’est-ce qu’une interaction ?
Quand un objet A agit sur un objet B, alors l’objet B agit sur l’objet A : c’est une interaction.
3° loi de Newton, principe des actions réciproques :
A une interaction entre un objet A et un objet B, correspondent deux forces : l’une, exercée par A sur B,
notée :
A/B
F
, la seconde, exercée par B sur A, et notée :
B/A
F
.
Ces deux forces sont telles que :
A/BB/A FF 
Elles ont donc la même norme, la même direction mais des sens opposés.
2.2. Interaction gravitationnelle
 Selon la loi de Newton, deux objet ponctuels A et B de masse
A
m
et
B
m
exercent l’un sur l’autre des
forces d’interaction gravitationnelle attractives dont la valeur est proportionnelle à chacune des masses et
inversement proportionnelle au carré de la distance AB qui les sépare.
La force exercée par un corps A sur un corps B est donnée par la relation vectorielle :
B/AAB
2BA
A/B Fu
AB
mm
GF 
. (1)
La valeur de ces forces d’interaction est donnée par
B/A
2BA
A/B F
AB
mm
GF 
.
A/B
F
est la force exercée par le corps A sur le corps B, unité : le newton (N).
G est la constante de gravitation universelle :
21311 .s.kgm 016,67G 
A
m
est la masse du corps A, unité : le kilogramme (kg).
B
m
est la masse du corps B, unité : le kilogramme (kg).
AB
est la distance entre A et B, unité : le mètre (m).
AB
u
est un vecteur unitaire de la droite passant par A et B et orienté de A vers B.
B/A
F
(action réciproque de
A/B
F
) est la force exercée par le corps B sur le corps A, unité : le newton (N).
A
m
B
m
AB
u
BA
F
AB
F
A
B
AB

Page 4/6 17/04/2017
 Cette relation est également valable pour des objets non ponctuels si la répartition des masses est à
symétrie sphérique (c'est-à-dire que la masse volumique ne dépend que de la distance au centre de
symétrie).
On considère que la masse de chaque corps est concentrée au centre de gravité du corps et dans ce cas la
distance AB est la distance séparant les centres de gravité de A et B.
La force calculée ainsi est la résultante de toutes les forces élémentaires agissant sur tout le volume des
corps.
A
m
A
AB
B
AB
u
B
m
B/A
F
A/B
F
 La portée de l’interaction gravitationnelle est infinie.
 Au voisinage de la surface terrestre :
On assimile la force de gravitation exercée par la Terre sur un corps A placé au voisinage de celle-ci au
poids de A (même si A n’a pas la symétrie sphérique) :
gmPF AAB/A
car
T2
T
M
Gg
(R ) 
avec
6
T
R 6,4 10 m
Le poids s’applique au centre de gravité de A.
 Application :
Calculer la valeur des forces d’attraction gravitationnelle qui s’exercent entre la Terre et la Lune. On
donne :
24
T
M 5,98 10 kg
;
kg1035,7M 22
L
;
km103,84D 5
L-T 
2
LT
LT
TLLT )(D MM
GFF
A.N. :
24 22
11
T L L T 82
5,98 10 7,35 10
F F 6,67 10 (3,84 10 )
soit
20
T L L T
F F 1,99 10 N  
.
2.3. Interaction électromagnétique
2.3.1. L’électrisation
 Au niveau microscopique : l’électrisation (Cf. 1S P 01 TP électrisation).
Un corps est électrisé lorsqu’il porte des charges électriques, il n’est donc plus électriquement neutre.
Un corps peut-être électrisé de différentes manières :
par frottement avec un autre corps initialement neutre électriquement,
par contact avec un autre corps électrisé,
par influence.
Électriser un objet consiste :
Soit à lui apporter ou arracher des électrons ;
Soit à provoquer un déplacement interne des charges électriques.
Lorsqu’on frotte A avec B, un des deux corps perd des électrons tandis que l’autre les capte.
Celui qui perd des électrons devient porteur d’une charge électrique positive (par défaut d’électrons) et celui qui capte les
électrons devient porteur d’une charge électrique négative.
Le verre, chargé positivement lorsqu’on le frotte avec de la laine, perd donc des électrons et le chiffon de laine en capte.

Page 5/6 17/04/2017
 Isolant : c’est un matériau dans lequel les électrons ne peuvent se déplacer que sur de très courtes
distances (inférieures à la taille des atomes).
Dans un matériau isolant, les électrons d’un atome sont donc toujours à son voisinage.
Des électrons arrachés à un endroit du matériau laissent localement un excès de charges positives.
Des électrons déposés par contact laissent localement un excès de charges négatives.
Exemples d’isolants : la plupart des matières plastiques (P.V.C., plexiglass , verre …)
 Conducteur : c’est un matériau dans lequel certains électrons (de un à quatre par atome, mais pas tous)
peuvent se déplacer librement dans tout le volume du matériau.
Un excès ou un défaut d’électrons produit par une électrisation se repartit sur toute la surface du matériau.
Exemples de conducteurs : tous les métaux (cuivre, aluminium, fer …)
2.3.2. L’interaction électrique entre deux corps chargés
 Les porteurs de charges :
Une entité de taille microscopique et qui peut se déplacer dans un conducteur est appelée « porteur de
charge »
Exemples : électrons de conduction dans les métaux, ions dans les solutions chimiques …
 La loi de Coulomb :
Au dix huitième siècle, la théorie de l’interaction gravitationnelle de Newton (Cf. § 1.) brillait par toutes les découvertes qu’elle
avait permise et jouissait à ce titre d’un prestige extraordinaire.
Charles COULOMB, grâce à une magistrale (et un peu trop parfaite) expérience (une poignée de mesures jamais reproduite à
cette époque), à son prestige personnel et à une formidable intuition énonce une loi qui permet de calculer les forces produites
par l’interaction électrique entre deux corps chargés électriquement.
Deux charges électriques
A
q
et
B
q
exercent l’une sur l’autre des forces d’interaction électrique dont la
valeur est proportionnelle à chacune des charges et inversement proportionnelle au carré de la distance AB
qui les sépare.
Cette loi est valable pour des charges ponctuelles ou pour des objets chargés de symétrie sphérique.
La force électrique ou coulombienne exercée par une charge A sur une charge B est donnée par la relation
vectorielle :
B/AA/B
2
BA
A/B Fu
AB
qq
kF 
La valeur de ces forces est
B/A
2BA
A/B F
AB
qq
kF 
A
q
étant la charge électrique portée par le corps A et exprimée en Coulomb (C).
B
q
étant la charge électrique portée par le corps B et exprimée en Coulomb (C).
AB étant la distance entre les centres des objets A et B.
A/B
u
est un vecteur unitaire (ou unité) de la droite passant par les points A et B.
k est une constante de proportionnalité :
SI109.C.kg.sm108,987k 92239  
.
Si les deux charges ont le même signe, l’interaction
électrique est répulsive.
Si les deux charges sont de signes contraires,
l’interaction électrique est attractive.
AB
A
B
AB
u
AB
F
BA
F
A
q
B
q
AB
A
B
AB
u
AB
F
BA
F
A
q
B
q