les méthodes d`analyse des circuits :
DEFINITIONS
Circuit, Eléments passifs, Eléments actifs
Branche, Noeud, Maille
LOI DE KIRCHHOFF
Loi des Noeuds
Loi des Mailles
Rappel
les méthodes d'analyse des circuits :
réseaux de Kirchhoff (exercices)
DEFINITIONS
Circuit
Il est constitué par un nombre fini d'éléments connectés entre eux.
Eléments passifs
C'est le constituant de base du circuit. Dans le cas présent ce sera soit une résistance,
soit une self, soit un condensateur. Il a 2 extrémités (bornes) A et B (d'où le nom de
dipôle) qui ont chacune un potentiel V et il est parcouru par un courant d'intensité I. Il
existe une relation entre l'élément, la différence de potentiel VA - VB (tension) entre les
2 extrémités et le courant qui circule dans l'élément. Selon l'élément considéré les
relations sont les suivantes :
résistance R :
VA - VB = R I
self L :
VA - VB = L dI./dt
condensateur C :
I = C d(VA-VB)/dt
Par convention la relation tension-courant aux bornes d'un élément passif sera positive
lorsque le courant I circule dans l'élément du point de potentiel le plus élevé (A) vers
le point de potentiel le moins élevé (B). Ceci par analogie avec l'eau d'une rivière qui
s'écoule d'amont (niveau le plus élevé) en aval (niveau le plus bas). Les éléments
précédents sont incapables de fournir de l'énergie, mais la self et le condensateur
peuvent restituer l’énergie qu’ils ont emmagasinée. Ainsi les appelle-t-on éléments
passifs.
Eléments actifs
Un circuit électrique a besoin d'énergie pour fonctionner. C'est le rôle des sources
indépendantes de tension et de courant dites éléments actifs. On parlera de sources
d’excitation du circuit.
Par convention, une source fournit de l'énergie à un circuit si le courant circule dans
l'élément du point de potentiel le moins élevé vers le point de potentiel le plus élevé.
Remarque.
Dans le cadre des exercices, la mesure des intensités de courant et des différences de
potentiel se fait respectivement avec des ampèremètres et des voltmètres idéaux. Ceci
amène à considérer dans le schéma du circuit étudié un ampèremètre comme un court-
circuit (tension à ses bornes nulle) et un voltmètre comme un circuit ouvert (courant
circulant nul).
Branche
Dans la définition la plus simple, un élément constitue une branche
Le courant circulant dans cette branche sera appelé courant de branche.
Noeud
De la même façon, on dit qu'une branche est terminée en chacune de ses extrémités
par un noeud.
A chaque noeud correspond un potentiel appelé potentiel de noeud.
En se tenant à ces définitions, on obtient dans un circuit un nombre de branches et de
noeuds qui peut être très important. On prendra souvent des définitions moins
restrictives : une branche peut comporter plusieurs éléments; un noeud correspond à la
connexion d'au moins 3 éléments entre eux.
Maille
Dans un circuit, une maille est constituée d'éléments connectés entre eux formant une
boucle fermée(ABCDEF),(ABEF)...
Une boucle ne passe pas deux fois par le même noeud sauf le noeud de début et de fin
de boucle.
Un élément n'apparait qu'un fois dans une maille.
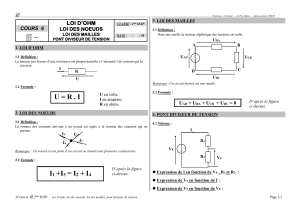
Loi des noeuds
La somme des courants entrant au noeud d’un réseau est égale à la somme des
courants sortant de ce noeud.
Loi des mailles
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
1
/
117
100%
