Equations et inéquations

Un parachutiste s'entraîne à effectuer des sauts de précision d'un avion volant à 4000 m d'altitude.
Chaque saut comporte deux phases:
_ une phase appelée " chute libre" ( parachute fermé puis séquence
d'ouverture du parachute ) ;
_ une phase " parachute ouvert " .
En prenant le mètre par seconde comme unité, la mesure de la vitesse acquise par le parachutiste est .
En prenant le mètre comme unité de longueur, la mesure de la perte d'altitude est h. Pour h inférieur à
400 m :
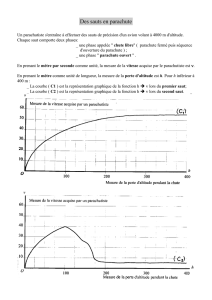
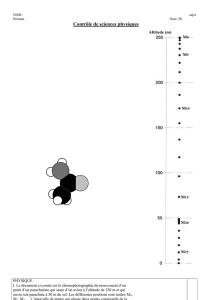
_ La courbe ( C1 ) est la représentation graphique de la fonction h   lors du premier saut;
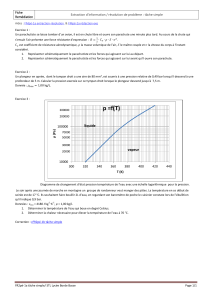
_ La courbe ( C2 ) est la représentation graphique de la fonction h   lors du second saut.
Des sauts en parachute

1 Lors de la phase de " chute libre " du premier saut, avant le déclenchement de l'ouverture du
parachute, la perte d'altitude est de 400 m.
1.1. Par une lecture du premier graphique, déterminer quelle semble être la vitesse (  ) acquise par
le parachutiste après une perte d'altitude de 100 m à partir du début du saut. Convertir cette
valeur en kilomètre par heure.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Par une lecture du premier graphique, déterminer au bout de quelle perte d’altitude ( h ) le
parachutiste atteint sa vitesse maximale.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3. Par une lecture du premier graphique, déterminer quelle semble être la vitesse maximale
atteinte par le parachutiste. Convertir cette valeur en kilomètre par heure
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4. Si par accident, le parachutiste ne pouvait ouvrir son parachute après avoir atteint sa vitesse
maximale.
1.4.1. Déterminer la hauteur de chute restante avant qu’il n’atteigne le sol.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4.2. Calculer le temps qu’il lui reste pour ouvrir son parachute en minutes ( mn ) secondes ( s ), à
la seconde prés, sachant que l’altitude minimum d’ouverture est de 30 m.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2 Lors de la phase de " chute libre " du deuxième saut, la perte d'altitude est inférieure à 400 m.
Dès le déclenchement de l'ouverture du parachute, la vitesse du parachutiste commence à diminuer.
2.1. Par une lecture du second graphique, déterminer quelle semble être la perte d'altitude du
parachutiste à l'instant où il déclenche l'ouverture de son parachute.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Par une lecture du second graphique, déterminer quelle semble être la vitesse acquise par le
parachutiste pour une perte d'altitude de 400 m. Convertir cette valeur en kilomètre par
heure.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Au début du saut, pour une perte d'altitude inférieure à 10 m, les mesures  et h sont liées
par la relation: 2 = 2 g h
Dans cette relation, g est la mesure de l'accélération de la pesanteur terrestre en prenant comme unité
le mètre par seconde carrée.
3.1. Calculer la mesure h ( en mètre ) de la perte d'altitude qui permet d'acquérir une vitesse de
5 m / s en prenant 9,8 m / s2 pour g. Exprimer cette perte d'altitude, arrondie au centimètre.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3. 2. Calculer la valeur  de la vitesse atteinte après une perte d’altitude de 3 m en prenant 9,8 m / s2
pour g. Exprimer cette vitesse en mètre par seconde ( au centième prés ) puis exprimer la en
kilomètre par heure. ( au centième prés ).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 A partir du second graphique et en supposant qu’il n’y aura plus de modification dans la chute
après 400 m.
4.1. Expliquer ce qui se passe entre 100 m et 175 m de chute.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2. Déterminer qu’elle semble être la perte de vitesse entre 100 m et 175 m de chute,
en mètre par seconde. Convertir cette valeur en kilomètre par heure.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3. Déterminer la hauteur de chute restant après 175 m.
Calculer le temps de chute " parachute ouvert " en minutes ( mn ) secondes ( s ).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

parachute a extraction manuelle - jusqu'a 160kg
Description sommaire:
C'est la possibilité de les déclencher a des hauteurs extrêmement basses qui confère aux parachutes
GALAXY tout leur attrait. L'essentiel, pour sauver le pilote, c'est que le parachute s'ouvre rapidement.
Cette ouverture rapide est obtenue grâce a une partie de la surface de la coupole qui ne laisse pas du
tout passer l'air et a des écopes d'extraction cousues sur tout le périmètre et le long de la sangle centrale.
La technique spéciale de pliage et le mécanisme d'ouverture (Brevet Galaxy) garantissent une utilisation
maximale de l'énergie employée par le pilote permettant l'extraction complète du parachute et son
ouverture immédiate. Les parois du container sont recouvertes d'une pellicule protectrice d'aluminium
anti-UV qui prolonge la durée de vie du parachute jusqu'a 25 ans.
Utilisations du parachute:
Parapentes, paramoteurs, deltas, et tous types d'ultralégers
Charge maximum (pilote et équipement)
poids surface Taux de Chute
GP 1/S 1.9kg(4.3 lbs) 90kg (200 lbs) 25m2 5.8m/sec
GP 2/S* 2.1kg(4.6 lbs) 110kg(240 lbs) 28m2 6.0m/sec
GP 3/S 2.3kg(5.1 lbs) 140kg(310 lbs) 32m2 6.2m/sec
GP 36/S 2.5kg(5.6 lbs) 160kg(350 lbs) 36m2 6.4m/sec
GP 40/SD 2,9kg(6.5 lbs) 190kg(423 lbs) 40m2 6.4m/sec
Vitesse maximum d'ouverture (a la charge maxi):
taille
U GP 1/S a GP 2/S 140km/h(90 mph) 22x22x10 cm
U GP 2/SD* 180km/h(115 mph)
U GP 3/S a 36/S 140km/h(90 mph) 28x23x11 cm
U GP 40/SD 180 Km/h(113 mph) 28x23x13 cm
Hauteur minimum d'ouverture (a 60 Km/h):
30 m pour toutes les tailles.
Structure de la coupole:
La coupole est de forme conique équipée de 14 suspentes extraites par une sangle centrale qui, dans un
premier temps, accélère le déploiement de la coupole, et dans un deuxième temps sert d'amortisseur de
l'impact a l'ouverture.
Accessoires:
Un harnais pour le pilote et deux mousquetons pour le container
Cycle de reconditionnement standard:
6 ans, pour une durée de service de 25 ans
Certification:
Aux normes ZS-2 LAACS