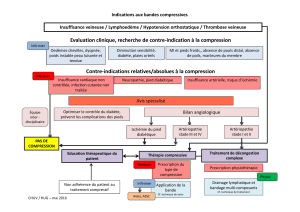
II - Méthodes de compression

CORITON Matthieu 14.06.00
BONNAUD Philippe Projet tutoré de maths
BONNET Jérémy La compression de données
JOURDAN Etienne
TROCHERIE Yvonic
BARBE Laurent
1

CORITON Matthieu 14.06.00
BONNAUD Philippe Projet tutoré de maths
BONNET Jérémy La compression de données
JOURDAN Etienne
TROCHERIE Yvonic
BARBE Laurent
2
Bien des gens ne comprennent rien à la compression de données -- comment peut-on
rendre quelque chose plus petit ? D'une certaine façon, on ne peut pas -- tout ce qu'on peut
faire c'est d'encoder les données de manière plus efficace. Nous allons essayer d’expliquer
quelques fondements et concepts entourant l'emmagasinage et la compression de données.
Ces concepts sont beaucoup plus simples que ce que les gens ont tendance à imaginer -- seuls
les détails d'implémentation sont complexes.
Fondamentalement, la compression de données sur ordinateur repose sur la recherche
de ressemblances (dans la forme ou dans le motif), afin d'enregistrer la description de la forme
ou du motif (en utilisant des tables ou des algorithmes mathématiques) plutôt que d'enregistrer
la donnée complète.
Nous allons voir dans un premier temps le but et les principes de la compression. Puis
nous présenterons les différentes méthodes de compression. Enfin nous exposerons quelques
problèmes liés à la compression.
I. But et principes de la compression
1-But
Le but de la compression est de mettre les informations sous un format tel qu’elles
occupent beaucoup moins de volume ( notamment pour accélérer le transfert sur les réseaux et
diminuer la taille occupée sur le disque). Les données, une fois compressées, ne sont plus
directement accessibles en tant que données cohérentes. Pour les récupérer, il suffit de les
décompresser, par l’algorithme inverse de compression, ce qui se fait généralement plus
rapidement que la compression. En fait, il n’existe pas un compresseur de données mais
plusieurs types de compresseurs qui correspondent à autant d’algorithmes différents.
Mais, on se rend compte rapidement que seulement quelques types de compressions sont
utilisés.
L’archivage des données a été un véritable problème du temps ou la capacité d’un
disque se comptait encore en quelques dizaines de Méga ( voire des kilos) . C’est à cette
époque que la compression est devenue un outil indispensable pour augmenter la capacité de
stockage et réduire les coûts de celle-ci. Aujourd’hui, nous pouvons stocker des Giga nos
disques et mis à part la sauvegarde de fichiers la compression n’est plus beaucoup utilisé pour
le stockage.
2-Principe
Le principe général est de supprimer ou du moins de réduire les redondances
d’informations par des formules mathématiques complexes pour rechercher les motifs qui se
reproduisent dans les données et les remplacer par des codes plus courts..Ainsi des méthodes

CORITON Matthieu 14.06.00
BONNAUD Philippe Projet tutoré de maths
BONNET Jérémy La compression de données
JOURDAN Etienne
TROCHERIE Yvonic
BARBE Laurent
3
ont été créé, comme la compression demi-octet ou encore la représentation topographique
binaire. Il s’agit là de vieilles méthodes qui n’existent plus de nos jours.
Pour utiliser un fichier compressé : il faut le décompresser avec un logiciel de
décompression compatible qui le reconvertit dans sa forme d'origine.
II - Méthodes de compression
1- RLE
RLE signifie Run Length Encoding, cette méthode est également appelée RLC pour
Run Length Coding, comme son nom l’indique le principe est de compacter les symboles
identiques consécutifs en utilisant un compteur. Cela nécessite un caractère d’identification
pour le compteur, le compteur et le caractère, soit 3 caractères. Bien évidemment, le caractère
d’identification ne doit pas apparaître dans le fichier source, sinon cela générerait des erreurs.
Cette méthode présente donc un gain de place seulement à partir du moment ou l’on trouve
plus de trois caractères identiques consécutifs. Cependant il existe des variantes a cette
méthode permettant de coder sur deux caractères seulement, comme dans le format d’image
PCX.
Exemple :
Soit une suite de caractère : AAAAABBCDDDEEEEEFFFFFFFFFF
La version compressée est : #5ABBC#3D#5E#10F
Ici le gain est de 11 caractères pour 26.
2-Huffman
Cet algorithme a pour but de repérer les suite de valeurs répétitives. A chaque suite
sera attribué un identifiant. Suivant la probabilité du motif, l'identitifiant sera plus ou moins
long (les motifs les plus courants auront un motif plus court)
On présente maintenant l'algorithme de Huffman sous une forme plus formelle en un
langage non informatique, en en faisant complètement abstraction des problèmes
d'implantation.
Les notations utilisées sont les suivantes :
n : nombre de motifs étudiées.
f(i) : fréquence du motif numéro i
T : Table des fréquences f(i)
p, s, k variables locales

CORITON Matthieu 14.06.00
BONNAUD Philippe Projet tutoré de maths
BONNET Jérémy La compression de données
JOURDAN Etienne
TROCHERIE Yvonic
BARBE Laurent
4
Exemple d’application :
La chaîne que nous allons traiter est :
BACFGABDDACEACG
Les motifs que nous allons étudier sont les octets, donc les lettres :
A, B, C, D, E, F, G
La table des fréquences est donnée ci-dessous: on constate que les motifs ont été écrits dans la
table par ordre décroissant de fréquence d'apparition.

CORITON Matthieu 14.06.00
BONNAUD Philippe Projet tutoré de maths
BONNET Jérémy La compression de données
JOURDAN Etienne
TROCHERIE Yvonic
BARBE Laurent
5
Ensuite commence la première étape de l'algorithme de Huffman. Son déroulement est
résumé ci-dessous dans la figure suivante. Il s'agit de regrouper les motifs de plus faible
fréquence comme suit : on additionne leurs fréquences et on place le nombre ainsi calculé
dans une nouvelle table où les deux fréquences ont été enlevé. On obtient une arboresence
dite "arborescence de Huffman".