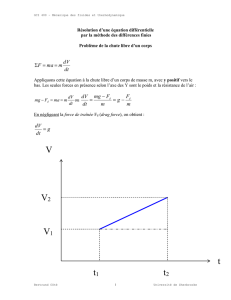
Facteurs - Université de Sherbrooke

GCI 400 - Mécanique des fluides et thermodynamique Bertrand Côté, ing., professeur
Département de génie civil 1 Université de Sherbrooke
GCI 400
Mécanique des fluides et thermodynamique
Conséquences de la variation de vitesse radiale
d’un écoulement laminaire dans une conduite circulaire
Vitesse moyenne V vs vitesse au centre U0 de la conduite (pp. 170-171)
RudAQ0
avec
rdrdA 2
rdr
R
r
UQ R 2)1( 2
2
00 
=
dr
R
r
rU )(2 2
3
0
R
R
rr
UQ
0
2
42
042
2
=
)
42
(2 22
0RR
U
=
4
22
0R
U
=
20
2U
R
La vitesse moyenne (dite aussi unidimensionnelle) dans la conduite est donc de :
20
U
A
Q
V
, soit 50 % de la vitesse au centre.
r
dA=2rdr

GCI 400 - Mécanique des fluides et thermodynamique Bertrand Côté, ing., professeur
Département de génie civil 2 Université de Sherbrooke
Facteur de correction pour la quantité de mouvement (p. 155)
Le fait d’utiliser la vitesse moyenne d’une conduite d’entrée/sortie plutôt que de tenir
compte de la variation de vitesse (nulle à la paroi et maxi. au centre) introduit une erreur
qui doit être compensée par un facteur de correction.
Le terme de flux de l’équation de transport de Reynolds est le suivant :
CS dAV)( nV
En tenant compte de la variation de la vitesse, il devient :
CS rdr
R
r
U
R
r
U 2)1()1( 2
2
0
2
2
0
Par transformations successives, il devient :
=
Rrdr
R
r
U0
2
2
2
2
0)1(2
=
Rrdr
R
r
R
r
U04
4
2
2
2
0)
2
1(2
=
Rdr
R
r
R
r
rU 04
5
2
3
2
0)
2
(2
=
R
R
r
R
rr
U
0
4
6
2
42
2
0)
64
2
2
(2 
=
)
622
(2 222
2
0RRR
U
=
6
22
2
0R
U
Comme il a été déterminé que U0 = 2V :
=
6
42 2
2R
V
=
22
3
4VR
=
2
3
4VA
ce qui explique le facteur de correction de 1.33 qu’on doit appliquer au terme V2A en
régime laminaire.
Facteur de correction pour l’énergie cinétique (pp. 170-171)
Le fait d’utiliser la vitesse moyenne d’une conduite d’entrée/sortie plutôt que de tenir
compte de la variation de vitesse (nulle à la paroi et maxi. au centre) introduit une erreur
qui doit être compensée par un facteur de correction.

GCI 400 - Mécanique des fluides et thermodynamique Bertrand Côté, ing., professeur
Département de génie civil 3 Université de Sherbrooke
Dans l’équation 3.65, le terme d’énergie cinétique vaut
m
V)
2
(2
.
Mais l’expression suivante serait plus rigoureuse pour tenir compte de la variation de
vitesse :
CS dA
V)(
2
2nV
=
CS dAV3
2
=
CS dA
R
r
U
3
2
2
0)1(
2
=
CS rdr
R
r
R
r
R
r
U 2)
33
1(
26
6
4
4
2
2
3
0
=
CS dr
R
r
R
r
R
r
rU )
33
(2
26
7
4
5
2
3
3
0
=
R
R
r
R
r
R
rr
U
0
6
8
4
6
2
42
3
086
3
4
3
2
2
2
=
)
86
3
4
3
2
(2
2
2222
3
0RRRR
U
=
)
8
(2
2
2
3
0R
U
Comme il a été déterminé que U0 = 2V, le résultat est :
=
)
8
(28
2
2
3R
V
=
AV3
=
VAV
2
=
QV
2
=
mV )( 2
ce qui explique le facteur de correction de 2 qu’on doit appliquer au terme
m
V)
2
(2
en
régime laminaire.