théorie KAM

Une introduction à la théorie
KAM
Application au système solaire ?
Philippe Robutel
IMCCE-CNRS-Observatoire de Paris

Kolmogorov énonce un théorème portant sur la stabilité des
systèmes hamiltoniens presque intégrables
1954 :
Moser puis Arnold en démontrent deux versions
1962, 1964 :
Une conséquence : “il est bien possible que le système solaire soit
quasi-périodique”
Et donc que les orbites des planètes soient stables
Plantons le décor

Kolmogorov énonce un théorème portant sur la stabilité des
systèmes hamiltoniens presque intégrables
1954 :
Moser puis Arnold en démontrent deux versions
1962, 1964 :
Une conséquence : “il est bien possible que le système solaire soit
quasi-périodique”
Et donc que les orbites des planètes soient stables
Plantons le décor

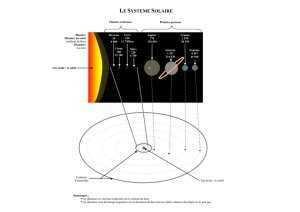
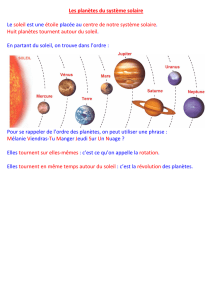
Kepler (1571-1630) : mouvements périodiques
a, e, I, !,⌦constants

Gravitation : Soleil + 1 planète : 2 corps --> Mouvement keplerien : stable
Interactions gravitationnelles entre les planètes (et les comètes) : les
perturbations s’accumulent et peuvent détruire le système !
Newton (1643-1727)
Soleil + n planète :
2 questions scientifiques fondamentales du XVIII :
- La loi de Newton régit elle bien le mouvement des planètes ?
- La stabilité du système solaire est elle garantie malgré les interactions entre
les planète ?