TP : Autour de l`exploit de Félix Baumgartner

Lycée Victor Hugo MP-MP*-PC-PC*-PSI 2016-17
TP : Autour de l’exploit de Félix Baumgartner
Le 14 octobre 2012, l’autrichien Félix Baumgartner a battu le record du saut le plus haut
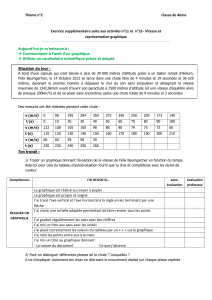
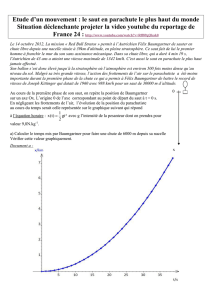
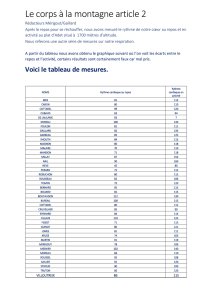
du monde 1, en s’élançant d’un ballon stratosphérique l’ayant amené à 39 068 m d’altitude (voir
la photo 1). Par ce même saut, il fut également le premier homme à dépasser le mur du son en
chute libre, avec une vitesse maximale de 1358 km/h 2. Le saut en chute libre eut une durée de
4 minutes et 19 secondes, Félix Baumgartner ayant ouvert son parachute à 2500 m d’altitude.
Parmi les préparations ayant permis de réussir cet exploit, on peut citer deux sauts de test :
- l’un en mars 2012 avec un départ de 21 818 m, avec une vitesse de pointe de 580 km/h,
- un autre en juillet 2012, de 29 456 m et une vitesse maximale de 805 km/h.
Ces deux sauts d’essai, comme prévu, n’ont pas permis d’atteindre une vitesse supersonique
puisqu’à très haute altitude (entre 10 et 40 km environ), la température de l’air est de l’ordre
de -50˚C et la vitesse du son vaut environ 300 m/s.
Figure 1 – saut de Félix Baumgartner à plus de 39 km d’altitude
Le but de ce TP est d’étudier la dynamique d’une chute libre à très haute altitude par une
méthode numérique. L’équation du mouvement n’ayant pas de solution analytique, on se propose
de la résoudre de manière approchée en utilisant dans un premier temps la méthode d’Euler.
Après affichage des courbes, les résultats seront ensuite exploités afin de déterminer la valeur de
différents paramètres (vitesse maximale, durée du saut...) et notamment de prédire à partir de
quelle hauteur il est possible de dépasser le mur du son en chute libre. Enfin, l’influence du pas
de temps sera examiné et analysé amenant à utiliser une méthode d’intégration plus efficace :
la méthode de Newmark.
1. Depuis, ce record a été battu en octobre 2014 par l’un des vices-présidents de Google, Alan Eustace, avec
un saut de 41 419 m.
2. Félix Baumgartner détient actuellement toujours le record de l’homme le plus rapide en chute libre puis-
qu’Alan Eustace n’atteignit "que" 1323 km/h.
1

Lycée Victor Hugo MP-MP*-PC-PC*-PSI 2016-17
I Mise en équation
On introduit les paramètres suivants :
— la masse du parachutiste, notée m,
— la pesanteur, considérée comme uniforme, notée g,
— la surface apparente du parachutiste (celle de son projeté sur un plan horizontal), notée S,
— le coefficient de traînée (grandeur sans dimension), noté cx,
— la masse volumique de l’air à l’altitude z, notée ρ(z).
On utilisera les valeurs numériques suivantes, proches de celles de Félix Baumgartner lors de ses
sauts : m= 130 kg, S= 1 m2et cx= 0,8.
Par ailleurs, on considérera un modèle d’atmosphère terrestre simplifié pour lequel :
ρ(z) = ρ0exp −z
Havec ρ0= 1,2 kg/m3et H= 7 km.
Lors de la chute libre, le parachutiste (équipé d’une tenue d’astronaute dans la mesure où il
évolue dans une atmosphère raréfiée) subit deux forces :
— la force de pesanteur (vers le bas),
— la force de frottement de l’air (opposée à la vitesse, donc vers le haut). L’écoulement
étant turbulent, cette force est proportionnelle au carré de la vitesse.
Ainsi en notant z(t)l’altitude du parachutiste et V(t)sa vitesse orientée vers le bas à la
date t, la loi de la quantité de mouvement s’écrit :
mdV
dt =mg −1 2ρ(z(t))ScxV2(t)avec V(t) = −dz dt
L’équation du mouvement est donc une équation différentielle scalaire du 2eordre par rapport
àz, qui peut aussi être vue comme une équation différentielle vectorielle du 1er ordre par rapport
au vecteur
~u(t) = z(t)
V(t)!
pouvant s’écrire sous la forme : d~u
dt (t) = −→
F(t, ~u(t)) où −→ Fdésigne la fonctionnelle, ici une
fonction de deux variables à valeurs dans R2. On peut noter qu’ici la fonctionnelle ne dépend pas
explicitement du temps t(correspondant à un problème de mécanique invariant dans le temps :
en effet, la date du saut n’intervient pas dans le problème !).
II Travail préparatoire
On indice par kla valeur des différentes grandeurs à la kème itération dans le cadre de la
résolution approchée de l’équation différentielle par la méthode d’Euler. On note pas le pas de
temps (constant) choisi pour la résolution.
1. Expliciter la fonctionnelle −→ F.
2. Rappeler le principe de la méthode d’Euler et expliciter les valeurs (donc les relations de
récurrence) de tk+1,zk+1 et Vk+1 en fonction de tk,zket Vket des autres paramètres.
3. Écrire en Python une fonction maxi prenant comme paramètre une liste de nombres et
retournant le maximum de la liste ainsi que l’indice (rang) indiquant où se trouve ce
maximum dans la liste (le plus petit indice s’il y en a plusieurs).
4. Écrire en Python la fonction rho donnant la masse volumique à l’altitude passée comme
paramètre.
2

Lycée Victor Hugo MP-MP*-PC-PC*-PSI 2016-17
III Mise en oeuvre de la méthode d’Euler
Créer la fonction euler ayant comme paramètre le pas de temps ainsi que l’altitude initiale
du saut et retournant trois listes contenant respectivement les temps tk, les altitudes zket les
vitesses Vk.
On considérera que le parachutiste part avec une vitesse initiale nulle et l’on choisit le début
du saut comme origine des temps. Par ailleurs, on arrêtera l’itération lorsque le parachutiste
atteint l’altitude à laquelle il ouvre son parachute, à savoir 2500 mètres.
IV Tracé des courbes
Créer une fonction courbes ayant comme paramètre le pas de temps et l’altitude initiale du
saut et affichant deux figures distinctes (à l’aide de la fonction figure) :
— l’une où sera tracée la courbe donnant l’altitude du parachutiste en fonction du temps,
— l’autre où seront tracées la courbe donnant la vitesse du parachutiste en fonction de
l’altitude ainsi qu’une ligne horizontale en pointillés indiquant la vitesse du son.
V Exploitation des résultats
Pour répondre aux questions suivantes, le pas de temps choisi sera égal à 1 s.
1. Créer une fonction analyse ayant en paramètre l’altitude initiale du saut et affichant sous
la forme d’une phrase (avec la fonction print) la vitesse maximale atteinte pendant le
saut (en km/h) ainsi que la durée de la chute libre. On utilisera la fonction maxi créée en
début de TP.
Comparer les résultats obtenus avec ceux présentés en introduction. Proposer une expli-
cation possible à l’écart observé.
2. Créer une fonction recherche affichant sous la forme d’une phrase l’altitude minimale du
saut pour que le parachutiste dépasse la vitesse du son lors de sa chute, ainsi que l’altitude
à laquelle cette vitesse est atteinte.
3. Enfin, créer une fonction dureesupersonique ayant comme paramètre l’altitude initiale
du saut et affichant sous la forme d’une phrase l’intervalle d’altitude dans lequel la chute
libre est supersonique ainsi que la durée de cette phase. Ne pas oublier de considérer le cas
où la chute libre n’est jamais supersonique.
VI Influence du pas de temps
On désire visualiser l’influence du pas de temps sur les solutions obtenues. Créer pour cela
une fonction comparaison ayant comme paramètre l’altitude initiale du saut et affichant une
seule figure contenant les courbes donnant la vitesse du parachutiste en fonction de l’altitude
obtenue pour les différentes valeurs de pas de temps suivantes : 11 s, 3 s, 1 s et 0,1 s. On utilisera
une boucle dans laquelle le pas de temps prend successivement les valeurs de la liste [11,3,1,0.1]
(interdiction de faire de "copier-coller" en changeant "à la main" la valeur du pas). On pourra
éventuellement accompagner chaque courbe d’un label permettant de les distinguer. Une syntaxe
possible pour tracer v(z)sans relier les points entre eux, avec le label pas = p secondes où pest
la variable désignant le pas, est la suivante : plot(z,v,’o’,label=’pas = %s secondes’%p)
Pour afficher les différents labels, il faut écrire legend() avant l’instruction show().
Commenter les différentes courbes et conclure sur le choix du pas de temps de la section
précédente. Que remarque-t-on pour un pas de temps de 11 s ?
3

Lycée Victor Hugo MP-MP*-PC-PC*-PSI 2016-17
VII Un schéma plus efficace : la méthode de Newmark explicite
A pas de temps fixé, il est possible d’utiliser des méthodes numériques d’intégration plus
stables et générant un écart par rapport aux solutions exactes de l’équation différentielle plus
faible comparé à la méthode d’Euler. On propose ici de mettre en oeuvre la méthode de Newmark
explicite (avec γ= 0) dont le schéma numérique appliqué à notre cas s’écrit :
zk+1 =zk−pas Vk−pas2
2dV dt t=tk
Vk+1 =Vk+pas dV
dt t=tk
1. Créer la fonction newmark ayant le même cahier des charges que la fonction euler et
utilisant les relations de récurrence précédentes.
2. L’instabilité observée avec la méthode d’Euler disparaît-elle en utilisant la méthode de
Newmark (pour le même pas de temps) ?
VIII Origine de l’instabilité
On cherche à comprendre l’apparition de l’instabilité observée pour la méthode d’Euler si
le pas de temps n’est pas suffisamment petit. On raisonne pour commencer sur un intervalle
de temps pendant lequel l’altitude varie peu. La vitesse de descente vérifie alors une équation
différentielle de la forme, avec Aet Bdeux constantes :
dV
dt =f(V) = A−BV 2
1. Montrer que la solution V(t) = VLest une solution stable. Exprimer la constante VL.
On suppose que V(t)est suffisamment proche de VLpour pouvoir remplacer f(V)par son
développement de Taylor en VLà l’ordre 1.
2. Montrer alors que la méthode d’Euler appliquée à cette équation différentielle avec une
condition initiale proche de VLentraîne que la suite définie par uk=Vk−VLest une suite
géométrique de raison r. Exprimer ren fonction de A,Bet du pas de temps pas.
3. En déduire la condition d’apparition de l’instabilité. Comparer à la situation observée.
4