l1 lp 103

L1 LP 103 – Cours d’optique géométrique –17/10/07 1/4
Université Pierre et Marie Curie - L1 - LP 103 - Année 2007-2008
Cours d'optique géométrique
[email protected]
Chapitre 5
Le principe de Fermat et ses conséquences
1. Notion de chemin optique
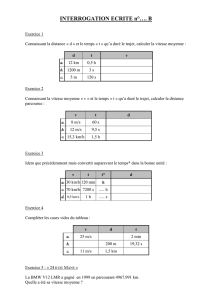
Soit deux points A et B (voir Figure 1). On appelle conventionnellement chemin optique la
distance algébrique :
ABAB cl
τ
±
≡
où AB
τ
est le temps mis pour la lumière pour parcourir le trajet AB et la c la vitesse de la
lumière dans le vide. Le chemin optique est défini positif lorsque le trajet correspond à rayon
réel et négatif lorsque celui-ci correspond à un rayon virtuel.
Le temps AB
τ
s’exprime comme : ∫
=)(rV
rd
AB r
r
r
τ
où rdr correspond à un déplacement infinitésimal tangent au point
r
r
à la courbe AB et )(rV
r
r
à la vitesse de propagation de la lumière au point
r
r
sur la courbe AB.
Le chemin optique s’exprime alors comme : rdrnrd
rV
c
lAB
rrr
r
r∫∫ == )(
)(
avec )(/)( rVcrn
r
r
r
≡ l’indice du milieu au point
r
r
.
Dans un milieu homogène ET isotrope, Cternrn
=
=
)()(
r
; dans ces conditions le chemin
optique vaut : ABAB dnrdnrdrnl === ∫∫
r
r
r)(
où AB
d est la distance parcourue par la lumière le long d’un des trajets AB.
B
A
rd
r
Figure 1

L1 LP 103 – Cours d’optique géométrique –17/10/07 2/4
2. Principe de Fermat
Supposons que pour aller d’un point A à un point B (voir Figure 1), la lumière puisse
parcourir différents trajets. A chacun de ces trajets est associé un chemin optique donné.
Le principe de Fermat (1601-1669), s’énonce ainsi :
« Pour aller d’un point A à un point B, la lumière choisit le chemin (en fait chemin optique)
qui minimise son temps de parcours ».
En fait le principe de Fermat, dans sa forme plus générale doit se formuler ainsi :
« Les trajets suivis par ka lumière sont ceux qui rendent le chemin optique stationnaire ».
Considérons deux trajets, C1 et C2, infiniment voisins et notons l1 et l2 les chemins optiques
associés respectivement à C1 et C2. Il y a stationnarité lorsque 0
21 =
−
≡
lll
δ
.
3. Conséquences
3.1. Milieu homogène et isotrope
On se place dans un milieu homogène et isotrope. Soit C un trajet donné pour aller du point A
au point B. Le chemin optique associé à ce trajet s’exprime dans ces conditions comme :
CC dnl =où C
d est la distance parcourue par la lumière le long du trajet C.
Selon le principe de Fermat, la lumière parcours le trajet qui rend le chemin optique
stationnaire, c'est-à-dire le trajet tel que 0
=
l
δ
; ce qui, dans un milieu homogène et isotrope,
revient à demander que :
∫== 0rdnl
r
δδ
On montre que parmi tous les trajets possibles, seule la droite qui relie A à B assure la
stationnarité du chemin optique.
Considérons le trajet, C’ infiniment voisin du trajet C et notons lC’ le chemin optique associé
au trajet C. Il y a stationnarité lorsque 0
'
=
−
≡
CC lll
δ
ce qui, dans un milieu homogène et
isotrope, revient à demander que 0
'
=
−
≡
CC ddd
δ
. Or parmi tous les chemins possibles, la
distance minimale est parcourue par la droite AB autrement dit la droite AB est le trajet qui
correspond à la distance minimale possible. La droite AB correspond au chemin minimal (ou
temps de parcours minimal), donc nécessairement au chemin optique stationnaire.
En vertu du principe de Fermat, la lumière se propage donc dans milieu étant homogène et
isotrope de manière rectiligne
3.2. Loi de la réflexion
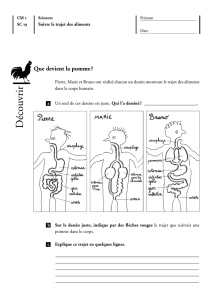
Le principe de la réflexion est illustré sur la Figure 2 dans le cas d’un dioptre plan séparant
deux milieux homogènes et isotropes.
Considérons de la lumière émise du point A de manière isotrope (source ponctuelle). Cette
lumière se propage dans un milieu homogène et isotrope d’indice n et selon la direction AM
(voir Figure 2). Le milieu étant homogène la lumière se propage selon des rayons rectilignes.
Parmi ces rayons, intéresseront nous à ceux qui passent par le point B donné.

L1 LP 103 – Cours d’optique géométrique –17/10/07 3/4
Notons que parmi les trajets allant de A à B, la droite AB correspond au trajet minimal (donc
stationnaire) et par conséquent, la droite AB correspond au trajet effectivement suivi par la
lumière pour aller de A à B. Cependant ce n’est pas l’unique trajet qui rende stationnaire le
chemin optique pour aller de A à B.
En effet, parmi les trajets possibles, supposons que le trajet allant de A à B en passant par M
soit aussi un trajet qui rende le chemin optique stationnaire.
Supposons maintenant un trajet infiniment voisin passant par le point M’ (Figure 2). La
différence de chemin optique entre ces deux trajets vaut donc :
(
)
(
)
MBBMAMAMAMBBAM lllllll
−
+
−
=
−= '''
δ
avec 'MMxd =
r
Or au premier ordre : dxunll AMAM
⋅
=−
r
'où u est le vecteur normé colinéaire à AM. De
même : )('
'dxunll MBBM −⋅=− r
où u’ est le vecteur normé colinéaire à MB.
Il vient alors :
)(' dxundxunl
−
⋅
+
⋅
=
r
r
δ
Puisque le trajet AMB est stationnaire, il vérifie 0
=
l
δ
; ce qui implique donc :
0)'(
=
⋅
−
xduu
r
r
r
Ceci reste vrai quelque soit la direction de xd
r
dans le plan du dioptre. Par conséquent le
faisceau réfléchi (selon la direction u’) est dans le plan passant par AM et orthogonal au
dioptre.
Soit i l’angle d’incidence et i’ l’angle de réflexion, la condition précédente implique donc :
dxixdudxixdu )'sin('.)sin(. =
=
=
r
r
r
r
soit )'sin()sin( ii
=
.
Ce qui implique donc i=i’.
On démontre donc les deux propriétés vérifiées par le rayon réfléchi (loi de Snell-Descartes
pour la réflexion).
AB
MM’
xd
r
n
r
i
i’
Figure 2
3.3. Loi de la réfraction
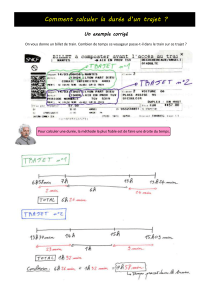
Le principe de la réfraction est illustré sur la Figure 3 dans le cas d’un dioptre plan séparant
deux milieux homogènes et isotropes. Notons n1 et n2 les indices de ces deux milieux.
On raisonne comme dans le cas de la réfration :
Supposons que le chemin optique AMB soit stationnaire ; celui-ci vérifie donc la condition :
(
)
(
)
0
'''
=
−
+
−
=
−= MBBMAMAMAMBBAM lllllll
δ

L1 LP 103 – Cours d’optique géométrique –17/10/07 4/4
On montre comme précédemment que :
(
)
(
)
xdunxdunlllll MBBMAMAM
r
r
r
r
'.. 21''
−
=
−
+
−=
δ
où u est le vecteur normé colinéaire à AM et u’ le vecteur normé colinéaire à MB.
La condition de stationnarité, 0=l
δ
, implique donc :
()
0.'
21
=
−
xdunun
r
r
r
Cette condition est vérifiée quelque soit xd
r
dans le plan du dioptre. Par conséquent le rayon
réfracté appartient au plan passant par AM et orthogonal au dioptre.
Soit i l’angle d’incidence et r l’angle de réfraction, la condition 0
=
l
δ
implique donc :
)sin()sin( 21 rnin
=
On a donc démontré les deux propriétés vérifiées par le rayon réfracté (loi de Snell-Descartes
pour la réfraction).
A
B
M
M’
xd
r
n
r
i
r
Figure 3