Gestion de l`énergie électrique dans l`habitat, cas du stockage

Gestion de l’énergie électrique dans l’habitat,
cas du stockage électrochimique
Hoang Anh DANG
1
, Caroline GUYON
2
, Benoit DELINCHANT
1
,
Patrick BEGUERY
2
, Frédéric WURTZ
1
1
G2Elab – Laboratoire de Génie Electrique de Grenoble
ENSE3, 11 rue des Mathématiques, BP 46, 38402 Saint Martin d’Hères
Email : [e-mail]
2
Schneider Electric, 37, quai Paul Louis Merlin, 38000 GRENOBLE
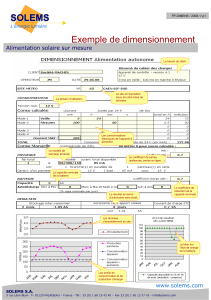
RÉSUMÉ . Aujourd’hui, la consommation électrique dans l’habitat – tertiaire occupe la
part la plus importante (60% - 70%) de celle totale en France. En parallèle de rechercher
des nouvelles sources énergétiques, nous nous intéressons aussi à la gestion de l’énergie
dans le bâtiment, surtout le cas du stockage électrochimique. Ainsi, nos travaux sont de
modéliser un modèle analytique de la batterie afin de simuler et optimiser la consommation
au réseau électrique suivant la demande de l’usager et le fonctionnement des sources
renouvelables.
ABSTRACT . Nowadays, the power consumption in home and building occupies the most
important portion (60% - 70%) of the total in France. Beside the new energy source
research, we are also interested in building energy management, especially electrical
storage. Therefore, our work is to model an analytical model of the battery for simulating
and optimizing the power consumption following the request of the user and the operation of
renewable source.
MOTS-CLÉS : énergie dans le bâtiment, gestion énergétique, stockage électrochimique,
batterie.
KEY WORDS : energy in building, energy management, storage electrochemical, battery.

XXX
e
Rencontres AUGC-IBPSA Chambéry, Savoie, 6 au 8 juin 2012 2
1. Introduction
Le programme HOMES développe des solutions innovantes de gestion de
l’énergie du bâtiment, selon deux principales stratégies :
- réduire la demande énergétique au niveau de chaque zone, en tenant compte
de son occupation,
- optimiser l’approvisionnement énergétique (production, distribution et
stockage).
Pour évaluer les potentiels de gains apportés par ces solutions, des modèles de
simulations d’une dizaine de bâtiments ont été développés à partir d’une évolution
de la toolbox Simbad et d’une bibliothèque d’environ 80 fonctions de contrôle.
Sur chacun des modèles il est possible d’activer tout ou partie des fonctions de
contrôle correspondant à trois niveaux de performances (manuel, expert ou optimal).
Concernant l’alimentation électrique du bâtiment, les solutions doivent prendre
en compte l’arrivée de configurations complexes comprenant tout ou partie des
éléments suivants :
- Sources d’énergie locale, dont on peut vendre ou consommer l’énergie
produite.
- Prix variables (achat, vente et consommation locale), connus 24h à l’avance.
- Protocole d’effacement de la charge.
- Batterie électrique fixe ou mobile.
Figure 1. Description du système bâtiment.

Titre de la communication. 3
Dans le cadre du programme HOMES, nous avons développé un modèle de
batterie électrique générique et adapté à la gestion afin de contribuer à simuler le
raccordement d’un véhicule électrique ou d’un pack de stockage dans le bâtiment
dans le but par exemple d’être associé à une source intermittente telle que la
production photovoltaïque [RIF 09].
2. Modèle d’une batterie électrique pour la gestion
2.1. Spécifications fonctionnelles
L’objectif du modèle est de simuler le fonctionnement de batteries aux différents
modes de scénario énergétique. La donnée d’entrée est la puissance de consigne
(Psp, positive en décharge, négative en charge) et les données sortantes sont la
puissance réelle de batterie (Pb), l’état de charge (SOC), les pertes de la batterie, la
puissance de décharge disponible et puissance de charge disponible.
Figure 2. Spécification du modèle de batterie.
Physiquement, les contraintes suivantes doivent être respectées :
- la puissance de décharge ne doit pas dépasser la puissance limite,
- la puissance de charge ne doit pas provoquer pas de surtensions (V ≤ V
max
)
- le courant de charge ne dépasse pas une valeur limite (I ≤ I
lim
).
Dans le cas d’une puissance de décharge ou de charge supérieure à la valeur
disponible, la batterie ne fournira que sa puissance disponible. En outre, afin de
préserver sa durée de vie, la batterie est isolée du réseau si son état de charge est très
faible (SOC
min
). Ces critères sont essentiels dans un modèle dédié à la gestion.
D’autres critères peuvent être associés à ce modèle, comme un « mode véhicule » qui
mettrait en indisponibilité la batterie et impacterait son état de charge lors de la
reconnexion (le véhicule a roulé).
Pour obtenir toutes ces informations, notre modèle doit d’abord fournir sa
puissance. Pour y parvenir nous allons passer par un modèle électrique équivalent de
la batterie et définir l’équation qui régie la tension à ses bornes.
P
sp
P
b
SOC
P
décharge_disp
Paramètres de batterie, état de charge
initial.
Batterie
P
décharge_disp
Pertes

XXX
e
Rencontres AUGC-IBPSA Chambéry, Savoie, 6 au 8 juin 2012 4
2.2. Modèle électrique équivalent
De nombreux modèles sont disponibles dans la littérature [RIF 09] [LAB 06]
[DEK 08] [TRE 08] pour répondre à des besoins de simulation fine ou rapide. Dans
notre cas, un modèle simple est recherché tout en répondant de façon la plus juste
aux sollicitations de charge et de décharge. Pour cette raison, nous choisissons
l’hypothèse proposée par Shepherd [SHE 63] comme la base de modélisation. Son
hypothèse s’appuie sur un schéma équivalent simple de batterie, une tension à vide
est mise en série avec une résistance variable.
V
OC
R
V
V
B
I
B
Figure 3. Schéma électrique équivalent.
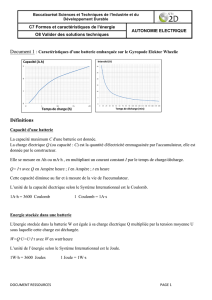
Ce modèle doit prendre en compte la variation de tension de batterie en fonction
de l’état de charge. En effet, la courbe caractéristique se compose de trois zones de
fonctionnement : zone exponentielle, zone nominale et zone de polarisation. (Figure
4)
Figure 4. Courbe typique de caractéristique à la décharge [TRE 08].
En synthétisant les trois phénomènes de décharge et les hypothèses de Shepherd,
nous pouvons rédiger l’équation de puissance au régime de décharge et de charge en
fonction de temps :
Au mode de décharge (P
B
≥0 et I
B
≥0) :
)(
2
max
2
0
max
QQB
BBBIBB
eIAI
Q
Q
KIRIVP
−
+−−= [1]

Titre de la communication. 5
Au mode de charge (P
B
≤0 et I
B
≤0):
)(
2
max
max
2
0
max
QQB
BBBIBB eIAI
QQQ
KIRIVP − +
−
−−= [2]
Avec :
)(
0OC
max
V
QQB
eAV
−
+= : Tension à vide (V)
Q
Q
KRR
IV max
+= : Résistance variable (Ω)
V
0
: Tension constante (V)
R
I
: Résistance interne (Ω)
K : Facteur de tension de polarisation (Ω)
I
B
: Courant de batterie (A)
Q
max
: Capacité maximale (Ah)
Q
0
: Charge initiale (Ah)
∫
−=
t
BC
dtIQQ
0
0
η : Charge instantanée (Ah)
η
C
: Rendement faradique
A : Facteur de tension (V)
B : Facteur de charge (Ah
-1
)
Ces équations nous permettent de déterminer l’état de charge (SOC), les
puissances disponibles (charge et décharge) et les pertes de la batterie.
3. Exploitation du modèle de la batterie
3.1. Validation du modèle unitaire
Le modèle a été développé pour supporter les types de batteries les plus
répandues (Plomb-acide, Ni-Cd, Li - ion, Ni-MH) et n’est paramétré qu’en fonction
de grandeurs nominales telles que la tension à vide et la capacité.
Batterie testée : Li-ion, 11.1 V, 6100 mAh, Q
0
=100%, Mode de charge rapide. Il
s’agit d’une batterie d’ordinateur portable. Les mesures sont obtenues par le logiciel
BatteryMon (v2.1, www.passmark.com).
Nous remarquons sur la Figure 5, que l’état de charge issu des mesures
correspond de manière quasi parfaite à l’état de charge calculé par le modèle. Ces
résultats sont obtenus avec une puissance de consigne définie par la puissance
mesurée. Notons malgré ces bons résultats que la tension calculée par le modèle, qui
n’est qu’un intermédiaire de calcul, ne correspond pas parfaitement à la tension
mesurée.