remerciements - Centre d`Etudes Biologique de Chizé

DIPLOME D’ETUDES APPROFONDIES
Biologie, Evolution et Contrôle des Populations
MEMOIRE DE RECHERCHE
Coexistence de deux espèces proches : rôles de
l’habitat, de la ressource trophique et du temps
Mémoire présenté par François Brischoux
Sous la direction de Xavier Bonnet
Centre d’Etudes Biologiques de Chizé
CNRS UPR 1934
79360 BEAUVOIR SUR NIORT
J
uin 2004

REMERCIEMENTS
Merci à Patrick Duncan pour m’avoir accueilli dans son laboratoire.
Merci à Xavier Bonnet pour m’avoir encadré, supporté, aidé, motivé ; avoir cru en moi. Merci pour
ce soutien permanent même si l’Australie est loin… Merci pour m’avoir accueilli à WoyWoy (dans
celui là, j’inclus évidemment Christine et les lardons…). Merci pour ces trois dernières années, en
espérant qu’on bosse ensemble les trois prochaines…
Merci à Olivier Lourdais qui m’a officiellement guidé pendant un peu plus d’une année mais qui a
fait beaucoup plus pendant beaucoup plus longtemps !!! Merci pour le plan Texas, pour nos premiers
papiers ensemble, pour les plans futurs. Merci de me pousser quand il le faut. Que notre collaboration
continue… Bonne chance pour le concours, ça va gazer.
Merci à Fred Lagarde pour être là, à l’écoute et puis donner un coup de main (souvent), pour le vin
du jura et la cochonnaille d’Italie, et puis pour le reste aussi…
Merci à Los Herpetos, ceux d’avant, que l’on ne revoit guère et c’est bien dommage et ceux de
maintenant, Hervé et Matthieu (mes p’tites hôtesses de forêt…), merci de me supporter en tant que
chef insupportable (!) et MathLaTortue, bonne chance à toi…
Merci à tous les étudiants du CEBC ou d’à coté, ceux avec qui on vit les uns sur les autres… Tim bien
sur, qui connaît sa place, ici comme ailleurs. Pierro, qui est toujours là et qui fait attention. Coraline,
qui sait pourquoi. Claire, pour la vraie vie. Marie pour la harpounette, Roger pour la gratte et à eux
deux pour les soirées musicales. Et tous ceux que je jette en touffe : Léo, Cyril & Marie, Maryline,
FredB, Maud, Seb, Diane, Loïc & Vero, David, Alex & Carole, LôRan, Rod, FredA, Maël,
Christine, Nadège, Thomas, Jalil, Star’Ac, Floflo, Cécile, Greg, Pierre, Yannig… Puis tous les
autres, ceux d’avant, à qui je pense de temps en temps…
Merci à Ivan Ineich pour avoir initié avec Xavier Bonnet cette étude calédonienne. Merci pour
m’avoir accepter au sein de la “Causus Team”. Merci aussi pour l’identification si rapide des murènes
et pour l'accès au fichiers data 2002, 2003 et data locomotion nécessaire pour les analyses.
Merci à Bernard Séret pour l’identification des murènes
Merci au Pr. Rick Shine, mon “parrain” de loin. Remets-toi bien de cette vilaine morsure…
Un grand Merci à l’Aquarium de Nouméa, en particulier à Claire Goiran et Philippe Leblanc, ainsi
qu’à toute l’équipe Jocelyn, Sylvain, Marie, Monique, Greg, Marc…
Merci à la Direction des Ressources Naturelles de la Province Sud, à François Devinck ainsi qu’à
Frédéric, Capitaine de l’Améré et à Christophe, Capitaine de l’Isabelle.
Merci à Vincent Liardet pour toute l’énergie qu’il a dépensé pour me trouver un “Vendredi”…
Merci à Eric, le rochellais calédonien, pour les bonnes discussions, le pain de marin (celui qui ne
durcit jamais…) et les pains aux raisins. Ca change des biscottes !!!!
Merci à Michel Kulbicki de L’Institut de Recherche et de Développement de Nouméa.
Merci à toute l’équipe des Plong’ Dem’ et notamment à Tanguy, Thierry et Richard. Merci pour
tous les craznas du midi et la One fraîche. Bon vent à vous…
Merci à la Société Calédonienne d’Ornithologie, à Nicolas Barré et toute son équipe. Merci pour le
barbecue et la bonne soirée.
Merci à Ivy pour avoir épargné la Nouvelle Calédonie et m’avoir offert une semaine de vacances à
Nouméa.
Merci enfin à mes parents dont le soutien permanent m’a permit d’aboutir jusque là…

CADRE GENERAL ET INTRODUCTION
Limiter la perte de la biodiversité est un des défis actuels majeurs, non seulement
pour des questions éthiques, mais aussi pour des raisons fonctionnelles ; les
écosystèmes appauvris deviennent fragiles et sont moins capables de résister aux
changements environnementaux (Barbault 1992, Ehrlich et Ehrlich 1981, Frank et Mc
Lawton 1994, Naughton 1991). Un autre défi, complémentaire du premier, est de
comprendre les phénomènes qui génèrent la biodiversité, notamment les processus
de spéciation et ceux qui permettent son maintien. En particulier, la coexistence
d’espèces proches à la fois sur les plans morphologique, génétique et écologique reste
mal comprise. L’intuition suggère que seule l’espèce la plus performante devrait
résister aux processus de compétition. A l’appui de cette notion, les cas de ruptures
de l’isolement géographique s’accompagnent de disparitions d’espèces par
compétition (Case 1991, Jaeger 1970). Inversement, l’isolement géographique est
considéré comme une des sources principales de la spéciation (Mayr 1963).
Pourtant les cas de coexistences d’espèces proches sont nombreux et soulèvent
des questions fondamentales. Par exemple, comment les mécanismes subtils qui
empêchent l’hybridation inter-spécifique (Shine et al. 2002c), résistent-ils au cours du
temps ?. Différents modèles théoriques fournissent des voies de recherche pour
comprendre comment des espèces proches coexistent malgré la promiscuité.
Toutefois, il existe peu d’études de terrain ayant permis de valider ou d’infirmer ces
modèles (Grant 1999, Schluter 1994). Ci-dessous sont présentés les concepts de
richesse spécifique et de coexistence puis les principales hypothèses alternatives
expliquant leur maintien, notamment lorsque les espèces concernées sont proches et
partagent le même écosystème.
La richesse spécifique (nombre d’espèces dans un milieu) fournit une mesure
de la biodiversité directement liée à la complexité des écosystèmes (Rosensweig
1996). Certains auteurs suggèrent que le maintien d’une forte richesse spécifique est
rendu possible par le biais de la coexistence (Hutchinson 1959). Ce concept a suscité
de nombreuses études en écologie des communautés depuis ces vingt dernières
années (Holt 1984, Kotler & Brown 1988, Kotler et al. 1993, Martin & Martin 2001).

Néanmoins, la reconnaissance des mécanismes de coexistence et leur compréhension,
restent souvent incomplètes du fait des lacunes taxonomiques et de la complexité
extrême des interactions entre les différentes espèces et de nombreux facteurs
abiotiques (Tokeshi 1999). Malgré la complexité des relations mises en jeu, deux
grands processus majeurs pourraient expliquer la coexistence des espèces (Tokeshi
1999) : i) la réduction de la compétition (en particulier de la compétition inter-
spécifique), ii) la prédation au sens large (c’est à dire englobant le parasitisme). Le cas
de la réduction de la compétition apparaît particulier car il met en jeu des processus
bien différents des processus de régulation des populations par prédation.
La coexistence implique très souvent des interactions fortes entre espèces,
notamment des interactions compétitives pour lesquelles deux espèces (au moins)
s’influencent négativement. Il existe trois conditions majeures pour reconnaître une
situation de compétition (Tokeshi 1999) : i) différentes espèces partagent les mêmes
ressources, ii) les ressources partagées sont en quantités limitées, et iii) les espèces
impliquées sont affectées défavorablement par chacune des autres espèces au cours
de l’acquisition de la ressource. Les situations de compétition présentent un grand
intérêt en écologie car c’est un des facteurs majeurs influençant la structure des
communautés (Begon et al. 1986, Tokeshi 1999).
Les bases mathématiques
Les interactions entre espèces restent très difficiles à appréhender. Comme souvent,
le passage par un système simplifié permet d’éclaircir certaines complications. Dans
ce cadre, la modélisation apporte des avantages très intéressants. Le modèle
théorique de Lotka-Volterra décrit le comportement de populations de deux
espèces compétitrices (Gotelli, 1998). Il s’agit d’un modèle simple et puissant,
développé dans les années 1920, qui reste fondamental dans l’étude de la
compétition en écologie (Gotelli 1998). Au départ, chaque population croît de façon
logistique avec chacune son propre taux de croissance et une capacité d’accueil
spécifique de l’environnement. La croissance populationnelle est réduite par la
compétition intra-spécifique mais aussi par la présence de la seconde espèce en
fonction du nombre d’individus compétiteurs. Ce modèle met aussi en jeu des

coefficients de compétition qui estiment respectivement les effets de l’espèce 1 sur
l’espèce 2 et inversement.
dt
dN1=
−−
1
211
11 K
NNK
Nr
α
, équation de la croissance de l’espèce 1
dt
dN 2=
−−
2
122
22 K
NNK
Nr
β
, équation de la croissance de l’espèce 2
où, N1 et N2 sont les tailles des populations, r1 et r2 les taux de croissance des
populations, K1 et K2 les capacités d’accueil de l’environnement, et  et  les effets
de l’espèce 2 sur l’espèce 1 et de l’espèce 1 sur l’espèce 2 respectivement.
La résolution des équations du modèle de Lotka-Volterra mène à quatre solutions.
Une de ces solutions met en jeu la prépondérance de la compétition intra-spécifique
par rapport à la compétition inter-spécifique (Harper 1978, May 1981, Rickleffs 1979).
Dans ce cas, il y a coexistence stable des espèces compétitrices (existence d’un point
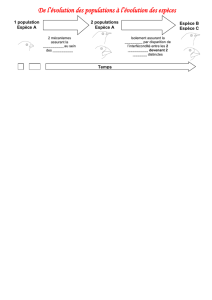
d’équilibre stable) : quelles que soient les abondances initiales des 2 espèces, les deux
populations vont atteindre une valeur d’équilibre (figure 1a). Néanmoins, chacune
des espèces persiste à une abondance plus faible qu’elle aurait atteinte en l’absence
du compétiteur. Dans ce cas, la compétition réduit les tailles de populations des deux
espèces mais ne mène pas à l’extinction de l’un ou l’autre des compétiteurs.
Les trois autres solutions du modèle mènent à la disparition de l’une ou l’autre des
espèces compétitrices. Deux de ces solutions sont analogues : soit l’espèce 1 “gagne”
la compétition (l’espèce 2 décline jusqu'à l’extinction et l’espèce 1 atteint la capacité
d’accueil de l’environnement) ; soit l’espèce 2 “gagne” la compétition (figure 1b et
1c). La dernière solution met en évidence un cas d’équilibre instable, les deux espèces
ne pouvant coexister à long terme et l’une est menée à l’extinction par l’autre (figure
1d). Il est cependant complexe de prédire l’espèce “gagnante”, car si la victoire
dépend de l’avantage numérique au départ, elle dépend aussi de bon nombre
d’autres paramètres (comme les taux de croissance des populations, par exemple).
Ces 3 solutions, qui mènent à la disparition d’un des partenaires de la compétition,
font appel au principe de l’exclusion compétitive.