Cours n°18 : Traitement, transmission et stockage de l`information

Dr A. Sicard CapeSup Grenoble Page 1
Cours n°18 : Traitement, transmission et stockage de l’information
Introduction
Suivre en direct à la télévision une compétition sportive qui se déroule à l’autre bout du monde,
envoyer un mail à un ami, transporter dans la mémoire d’un baladeur MP3 des centaines d’heures de
musique..., tous ces gestes peuvent paraître aujourd’hui anodins, voire naturels. Mais la maîtrise par
l’Homme de la transmission et du stockage de l’information ne s’est pas faite en un jour et réserve
encore sans doute nombre d’innovations futures.
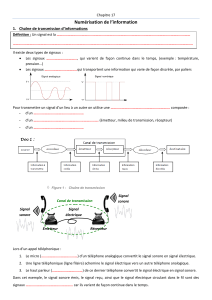
1) Chaîne de transmission de l’information
1.1) Principe de la transmission de l’information
L’acte de communiquer, c'est-à-dire transmettre une information, est au centre des activités
humaines. Lorsqu’un individu veut transmettre une information à un autre en lui parlant
directement, on peut schématiser la chaîne de transmission de cette information ainsi :
La source est ici la voix de l’individu contenant l’information à transmettre, le canal de transmission
est l’air, milieu matériel qui permet la propagation du son, et le récepteur est le système auditif de
l’interlocuteur qui va pouvoir capter le message envoyé.
1.2) Codage et décodage
Le mode de communication verbale directe atteint toutefois rapidement ses limites notamment
lorsqu’il s’agit de transmettre des informations à grande distance. L’utilisation d’instruments de
musique puissants (cor, tam-tam…) ou de signaux de fumée a permis il y a bien longtemps de
s’affranchir de cette limite. L’introduction d’un codage (et donc d’un décodage côté récepteur) est
alors devenue nécessaire afin de transmettre des messages à plusieurs kilomètres alentours.
Par exemple, un message d’alerte est codé en une succession déterminée de coups donnés sur un
tam-tam. Ce message codé transite par l’air (le canal) avant d’arriver aux oreilles du récepteur qui
pourra alors le décoder (à condition de connaître le code !) afin d’acquérir l’information envoyée par
la source : « alerte » !
Source
Canal
Récepteur
Source
Canal
Récepteur
Codage
Décodage

Dr A. Sicard CapeSup Grenoble Page 2
2) Numérisation
2.1) Signaux analogiques et numériques
2.1.1) Signaux analogiques
Les capteurs convertissent la valeur d’une grandeur physique quelconque (pression, température,
vitesse, etc.) en un signal électrique (une tension ou une intensité) analogique.
Un signal analogique est un signal continu dont la mesure à un instant donné peut théoriquement
donner un nombre réel quelconque. Ce signal est donc mesurable à tout instant et peut prendre un
nombre infini de valeurs différentes.
Par exemple, un microphone captant un son le transforme en une tension électrique évoluant au
cours du temps. La courbe représentant ce signal est continue et présente une infinité de valeurs
différentes : il s’agit bien d’un signal analogique.
2.1.2) Signaux numériques
Un signal numérique n’est pas continu et le nombre de valeurs qu’il peut prendre n’est pas infini. On
ne peut donc pas mesurer ce signal à n’importe quel instant et cette mesure ne pourra prendre
qu’un certain nombre de valeurs différentes. Voici à quoi pourrait ressembler le signal
précédemment enregistré par le micro s’il était de nature numérique (micro USB par exemple) :

Dr A. Sicard CapeSup Grenoble Page 3
2.2) Fichier numérique
Pour faire subir un traitement informatique au signal (enregistrement, analyse, etc.), il est nécessaire
de disposer d’un fichier numérique qui seul pourra être traité par un ordinateur.
Un fichier numérique est une succession de nombres binaires appelés bits. Un bit (pour BInary digiT)
est le plus petit élément d’information stockable par un système numérique (ordinateur, CD, etc.).
Un bit ne peut prendre que deux valeurs (0 ou 1) correspondant à deux états possibles d’un élément
de circuit électrique (tension haute ou basse). Les informations numériques sont codées en langage
binaire.
Chaque bit pouvant prendre la valeur 0 ou 1, N bits codent  entiers de  à 
. Ainsi,  bits constituent un octet qui permet de coder  entiers
de  à . En conséquence, le signal numérique ne peut prendre que des valeurs bien
définies, en nombre limité.
Par exemple, le codage en langage binaire du nombre  sur  bits est  car :
Le nombre de bits constituant un fichier numérique est généralement compté en multiples de l’octet.
Unité
Symbole
Valeur
1 kilooctet
1 ko
1024 octets
1 mégaoctet
1 Mo
1024 kilooctets
1 gigaoctet
1 Go
1024 mégaoctets
1 téraoctet
1 To
1024 gigaoctets
2.3) Conversion analogique-numérique
2.3.1) Principe de la conversion
Les signaux naturels (sons, images,…) sont de nature analogique, et nos capteurs sensoriels (yeux,
oreilles,…) fonctionnent eux aussi de façon analogique. Pour permettre à un système informatique
de traiter un signal en provenance d’un capteur par exemple, il faut d’abord recourir à une
conversion analogique-numérique. On doit donc procéder à la numérisation de ce signal. La
numérisation des signaux est omniprésente, car les signaux numériques peuvent être manipulés de
façon plus simple et plus fiable. De plus un signal numérisé peut être transmis plus rapidement et son
stockage requiert moins de place que celui d’un signal analogique.
Pour numériser un signal analogique , c’est-à-dire le transformer en un fichier numérique, il faut
recourir à un convertisseur analogique-numérique ou « CAN ». Cette numérisation comporte deux
étapes : l’échantillonnage et la quantification.
2.3.2) Echantillonnage
L’échantillonnage consiste à capturer les valeurs prises par un signal analogique à intervalle de temps
régulier. Le CAN opère donc un échantillonnage du signal  en prélevant à intervalle de temps
régulier , les valeurs  où  est un entier.

Dr A. Sicard CapeSup Grenoble Page 4
La fréquence d’échantillonnage, exprimée en hertz, est le nombre de valeurs capturées par le CAN
par seconde. La fréquence d’échantillonnage s’exprime comme :
Elle doit être suffisamment grande pour pouvoir reconstituer convenablement les variations du
signal analogique d’origine. Ainsi, plus cette fréquence est élevée et plus le signal numérique sera
précis.
Si la fréquence d’échantillonnage est insuffisante, on perdra une grande partie des informations
fournies par le signal analogique original. On parle alors de sous-échantillonnage.
Ainsi, si on veut utiliser un signal échantillonné, il faut être sûr que celui-ci contienne toute
l'information du signal analogique d'origine. Il est souvent commode de considérer celui-ci comme
une somme de sinusoïdes (cf. analyse spectrale). Or il est intuitivement évident qu'une perte
d'information se produit si le pas d'échantillonnage est trop grand par comparaison avec les périodes
en cause, la fréquence d'échantillonnage étant trop faible par rapport aux fréquences considérées.
Théorème de Shannon
Pour qu'un signal ne soit pas perturbé par l'échantillonnage, la fréquence d'échantillonnage doit être
supérieure au double de la plus haute fréquence  contenue dans le signal. Cette fréquence
limite s'appelle la fréquence de Nyquist.
La fréquence d’échantillonnage  doit donc vérifier :
L’intervalle de temps minimum entre deux prises de mesure correspondant à cette condition est :
2.3.3) Quantification
A chacune des dates d’échantillonnage, le CAN opère en outre une quantification : il produit  bits
qui représentent la valeur du signal analogique . Dans une gamme , le CAN va
faire appel à  niveaux de quantification pour coder les valeurs du signal.

Dr A. Sicard CapeSup Grenoble Page 5
Par exemple, si  bits,  correspond au niveau de quantification codé par  et  celui
codé par .
Quantifier la valeur du signal , c’est définir un nombre binaire dont le niveau est le plus
proche possible de .
Sur la figure suivante, le niveau le plus proche de  correspond au nombre binaire  (5 en
décimal).
La quantification du signal analogique va donc introduire une perte d’information.
La plus petite variation de tension que peut repérer un CAN est appelée résolution ou pas du
convertisseur. Le pas de quantification est donné par :
Plus  sera grand et meilleure sera la qualité de la quantification. Si  est fixé, par construction du
CAN par exemple, c’est  qui doit être le plus faible possible. Cela peut être réalisé en
choisissant, parmi celles possibles, la gamme  encadrant au plus près l’évolution du
signal analogique.
De manière générale, on pourra retenir que la qualité de la conversion analogique-numérique
augmente avec la fréquence d’échantillonnage et le nombre de bits de numérisation.
3) Images numériques
3.1) Création d’un fichier image à partir d’une image
Contrairement aux images réelles, constituées d’une infinité de points pouvant avoir un nombre
infini de couleurs, les images manipulables à l’aide de l’informatique sont numériques. Un appareil
photographique numérique, tout comme un scanner assure la numérisation d’une image. Pour cela,
l’appareil découpe l’image en un quadrillage ou trame. Chaque case s’appelle pixel (de l’anglais
picture element). A chaque pixel, on affecte un nombre binaire correspondant à la couleur de la case.
Un fichier image est ensuite produit qui permet d’avoir accès au nombre binaire associé à chaque
pixel.
La résolution d’un scanner est une mesure de la précision de la numérisation et s’exprime en point
par pouce (ppp) où 1 pouce vaut 2,54cm.