Les quadrilatères

Les quadrilatères (rappels)
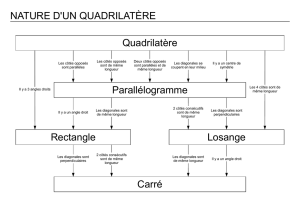
Le parallélogramme Le rectangle Le losange Le carré
Définition. Ses côtés opposés sont
parallèles .
Ses quatre angles sont droits . Ses quatre côtés ont la même
longueur
Ses quatre côtés ont la même
longueur et ses quatre angles sont
droits .
Propriétés des
diagonales.
Ses diagonales se coupent
en leur milieu
Ses diagonales se coupent en
leur milieu et ont la même
longueur .
Ses diagonales se coupent en
leur milieu et sont
perpendiculaires .
Ses diagonales se coupent en leur
milieu, ont la même longueur et
sont perpendiculaires .
Propriétés des
angles.
Les angles opposés ont la
même mesure.
Les angles sont droits. Les angles opposés ont la même
mesure.
Les angles sont droits.
Quelques
caractérisations
(méthodes pour
montrer qu’un
quadrilatère est
un...).
C’est un quadrilatère dont
les côtés opposés sont
parallèles .
C’est un quadrilatère dont
les diagonales se coupent
en leur milieu.
Deux vecteurs égaux AB et
DC définissent un
parallèlogramme.
C’est un quadrilatère dont les
quatre angles sont droits .
C’est un quadrilatère dont les
diagonales se coupent en leur
milieu et ont la même longueur
.
C'est un parallélogramme
ayant un angle droit .
C'est un parallélogramme
ayant les diagonales de même
longueur.
C’est un quadrilatère dont les
quatre côtés ont la même
longueur.
C’est un quadrilatère dont les
diagonales se coupent en leur
milieu et sont perpendiculaires .
C'est un parallélogramme ayant
deux côtés consécutifs de la
même longueur .
C'est un parallélogramme ayant
les diagonales perpendiculaires.
C’est un quadrilatère dont les
quatre côtés ont la même longueur
et dont les quatre angles sont
droits.
C’est un quadrilatère
dont les diagonales se coupent en
leur milieu, ont la même longueur
et sont perpendiculaires .
C'est un rectangle ayant deux côtés
consécutifs de la même longueur .
C'est un losange ayant un angle
droit .
Vous pouvez utiliser ce tableau à chaque fois que vous avez besoin des propriétés d’un quadrilatère ou quand vous voulez montrer qu’un quadrilatère est
particulier.