Les Hacheurs Convertisseurs DC-DC : Guide Technique

LES HACHEURS
CONVERTISSEURS DC- DC

V.1 Introduction
Les hacheurs fonctionnent à l'aide de la commutation forcée. Ils permettent d’obtenir une tension
continue de valeur moyenne variable (Uch) à partir d’une source de tension continue fixe (Us). C’est
un convertisseur continu- continu (tension  continue – tension continu variable Uch), il est
representé comme illustré sur la figure 1:
Figure 1 Convertisseur continu - continu
Les hacheurs sont très utilisés dans la traction électrique à courant continu (traction pour chemin de
fer), trolleybus, chaine de conversion dans les énergies renouvelables, source de tension continue,
véhicule à batterie et le réglage de la vitesse des moteurs à courant continu.
Remarque :
L’utilisation du thyristor dans les hacheurs est très délicate car l’annulation du courant au blocage
n’est pas naturelle. Il est nécessaire de bloquer ce dernier par l'utilisation d'un circuit de commutation
forcée (besoin de deux circuit un pour l'allumage et l'autre pour le blocage). Le circuit de blocage
comprend plusieurs thyristors additionnels, inductances et condensateurs pour parvenir au blocage du
composant principal. C'est pour cette raison qu'il est préférable d'utiliser les transistors de puissance
(IGBT, MOSFET) pour les petites et moyennes puissances et parfois les GTO (Gate Turn Off) pour
les moyennes et les fortes puissances. Mais pour les très fortes puissances, l'utilisation de thyristor est
inévitable.
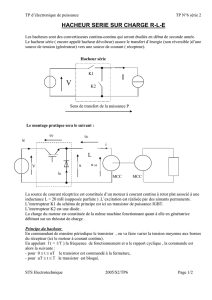
V.2 Hacheur dévolteur (série, Buck converter)
V.2-1 Débit sur charge résistive
Figure 2 schéma de puissance du hacheur dévolteur (charge résistive)
R
_
+
Vs

Figure V.3 tension de charge (Vch, Ich et Vtr)
Le courant s’annule instantanément dès que le transistor est bloqué à t= α.T
Avec :   
 (il ne faut pas confondre la fréquence de hachage fH (500 Hz - 1000 Hz), fréquence
du réseau (50 Hz)
αT : temps de fermeture (conduction)
 temps d’ouverture
α est le rapport entre le temps de conduction et la période de hachage ; il est appelé rapport cyclique :
 , α varie entre 0-1
Le hacheur fonctionne en deux modes, mode 1 hacheur fermé et mode 2 hacheur ouvert
Quand  est fermé : 0 
Quand  est ouvert :  
 d'ou t/T = α (1)
 (2)
1. Hacheur serie avec une charge résistive inductive
Il est à noter qu'avec la charge résistive inductive le courant ne peut pas être bloquer au moment
d'ouverture de l’interrupteur Tr. C’est pourquoi il est nécessaire de placer en parallèle avec la charge
Vs
αT
T
(1+α)T
2T
t
t-on
t-off
t-off
t-on
αT
T
2T
0
0
t

une diode à roue libre (freewheel diode)  comme illustré sur la figure 4.
Figure 4 schéma de puissance d'un hacheur série avec charge RL
Figure 5 
tension de charge Uch, courant de charge Ich, courant du transistor ITr, courant de la diode ID,
tension inverse du transistor (VTr) et tension inverse de la diode (VD)
0
αT
T
αT
T
0
0
αT
T
U
s
2T
2T
2T
(1+α)T
(1+α)T
(1+α)T
0
αT
T
(1+α)T
2T
0
αT
T
(1+α)T
2T
U
s
U
s
D
R
_
+
L
Vs

 Mode 1 le transistor conduit (fermé), le fonctionnement est comme suit:
- 0 t est fermé (la conduction de  force le blocage de la diode D) c.a.d l'anode de
la diode est négative la cathode est positive
  pour déterminer l'équation du courant il faut résoudre l'équation par
l'utilisation des transformés de Laplace ou la méthode simple du courant dans un circuit
électrique ou l'équation du courant i(t) généralement est composé de: la composante continue, la
composante alternative et la composante exponentielle
i (t) = Ic + Ia + Ae-t/τ
Dans notre cas l'interrupteur (transistor Tr) est fermé donc la diode se comporte comme un
interrupteur ouvert
- La composante alternative Ia = 0, notre circuit ne possède aucune alternative
- Une source continue existe dans notre circuit (Us) donc la composante continue Ic = Us/R
- La composante exponentielle existe parce que la constante du temps est différente de zéro
(notre circuit possède une résistance R et une inductance L), τ = L/R
i1 (t) = Us/R + A.e-t/τ (3)
- La constante d'intégration A est déterminée à partir des conditions initiales:
t=0 , i1(t) = I0 (voir la figure 5)
on substituant dans l'équation 3 on obtient la valeur de la constante A
I0 = Us/R + Ae0 donc A= I0 - Us/R
+(
 , avec   
 (4)
à    on a :  
+(
 (5)
 Mode 2, le transistor est ouvert, le fonctionnement est comme suit:
   est bloqué (le courant circule en roue libre dans la diode et la charge)
La composante continue Ic et la composante Ia sont nulles
A partir des conditions initiales,  t =  , i2 (t) = 