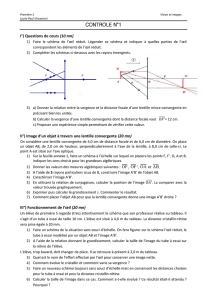
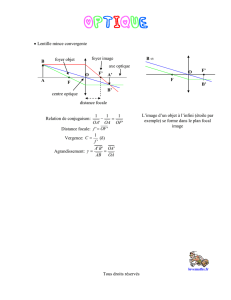
TD Lentilles Minces : Optique Géométrique - Exercices et Constructions

EXERCICE 1 - Rayons émergents
EXERCICE 2 - Construction d’images
1. On considère une lentille mince convergente , de centre optique et de distance focale
.
1.1. Construire l'image d’un objet réel (taille 1 cm) situé à 2,0 cm du centre optique
.
1.2. Construire l'image d'un objet virtuel (taille 1 cm) situé à 4,0 cm du centre
optique .
L
O
f′ = 4,0 cm
A′ B′
A B
O
A′ B′
A B
O
TSI 1 - TD Lentilles minces
Page sur 1 6
Thème 1
Ondes et
Signaux
Lentilles minces - TD 3
Echauffement
F’
F
6.
1.3. Construire l’image d’un objet situé à l’infini.
2. Soit une lentille mince divergente , de centre optique et de distance focale .
2.1. Construire l’image d’un objet réel de taille 2,0 cm situé à 8,0 cm de .
2.2. Construire l’image d’un objet virtuel de taille 2,0 cm situé à 4,0 cm de
2.3. Construire l’image d’un objet virtuel de taille 1,0 cm situé à 2,0 cm de .
On pourra vérifier les constructions à l'aide de la simulation disponible sur le site de la classe
(Physique → Optique géométrique → Construction image - Simulation)
EXERCICE 3 - Relation de conjugaison et grandissement
Dans chacun des cas de l’exercice précédent, retrouver par le calcul la position et la taille de
l’image .
EXERCICE 4 - Antécédent d’une image (✯)
Soit une lentille mince de distance focale dont on choisira la valeur.
Dans les cas suivants, construire l'objet conjugué, de l'image :
1. Lentille convergente ( )
1.1. Image réelle entre et .
1.2. Image virtuelle avant .
2. Lentille divergente ( )
2.1. Image virtuelle entre et .
2.2. Image réelle après .
EXERCICE 5 - Soirée diapo (✯)
1. On souhaite projeter sur un écran l'image d'une diapositive de taille 24 mm × 36 mm à l'aide
d'une lentille de focale . L’écran étant à 5,0 m derrière la lentille, préciser la position de la
diapositive et les dimensions de l'image nette sur l’écran.
2. On veut maintenant obtenir une image 40 fois plus grande que l'objet. L’objet et le projecteur
restant fixes, indiquer dans quel sens et de quelle distance il faut déplacer l'écran.
A′ B′
A B
L
O
f′ =−4,0 cm
A′ B′
A B
L
A′ B′
A B
L
A′ B′
A B
L
A′ B′
f′
A B
A′ B′
f′ > 0
O
F′
F
f′ < 0
F′
O
F
f′ = 8,0 cm
TSI 1 - TD Lentilles minces
Page sur 2 6
Entraînement

EXERCICE 6 - Vérification expérimentale de la relation de conjugaison de Descartes
(✯✯, !)
On place, sur un support, un objet à la graduation « » d'un banc d'optique (l'objet, constitué d'une
lettre imprimée sur un papier calque, est éclairé de façon à pouvoir observer une image).
On place alors une lentille convergente sur un deuxième support et un écran sur un troisième. Les
trois supports étant sur le banc, on déplace l'écran de façon à observer une image nette. On relève alors
la graduation de la lentille et celle de l'écran. On obtient":
1. Déterminer la vergence de la lentille utilisée assortie de son incertitude, calculée grâce
au programme Python disponible sur le site de la classe : https://physiquetsi1vieljeux.wordpress.com/
optique-geometrique/. Compléter le programme en remplaçant les … par les valeurs ou expressions
convenables. On pourra se référer au cahier Python et au document Mesure et incertitude.
2. On peut associer un diaphragme à la lentille sur son support. Quel est son effet"? Est-ce
judicieux pour ces mesures expérimentales"?
0
x1
x2
V=1
f′
TSI 1 - TD Lentilles minces
Page sur 3 6
import numpy as np
import matplotlib.pyplot as plt
x1 = np.array([...]) # Crée un tableau pour stocker les valeurs de x1 (en cm)
x2 = ... # Crée un tableau pour stocker les valeurs de x2 (en cm)
D_objet = ... # Calcul des valeurs expérimentales de la distance lentille-objet (en m)
D_ecran = ... # Calcul des valeurs expérimentales de la distance lentille-écran (en m)
vergence = ... # Calcul des valeurs expérimentales de la vergence (en dioptries)
Vergence = np.mean(...) # Calcul de la valeur moyenne des vergences
expérimentales
print("La vergence de la lentille utilisée vaut:", Vergence,"dioptries.") # Affiche la!
vergence.
u = np.std(vergence, ddof = 1) # Calcul de l'incertitude expérimentale sur UNE valeur de!
la vergence
n = len(x1) # Nombre n d'observations réalisées
incertitude = ... # Calcul de l'incertitude sur la moyenne des n
observations réalisées
print("L'incertitude sur le vergence de la lentille utilisée vaut: {:.1e}
dioptries.".format(incertitude)) # Affichage de l’incertitude.
plt.hist(vergence, bins = 'auto', color = ..., edgecolor = ...) # Crée l'histogramme!
de répartition des!
valeurs de la!
vergence
plt.title(...) # Donne un titre au graphique
plt.xlabel(...) # Donne un titre à l'axe des abscisses
plt.ylabel(...) # Donne un titre à l'axe des ordonnées
plt.show() # Affiche le graphe
9,0
10,0
11,0
12,0
13,0
15,0
20,0
25,0
30,0
40,0
50,0
79,2
51,1
41,0
37,3
33,0
32,1
33,2
36,9
41,1
50,3
59,8
(cm)
x1
(cm)
x2
EXERCICE 7 - Pouvoir séparateur de l’œil (✯)
Le pouvoir séparateur d'un œil emmétrope est , c'est-à-dire que deux points
peuvent être vus distinctement si leur écart angulaire est supérieur à cette valeur.
1. Jusqu'à quelle distance cet œil peut-il distinguer deux traits parallèles séparés de "?
2. Quelle doit être la taille d'une lettre d'un panneau autoroutier pour être lue à 250 m"? (Faire
l'étude avec la lettre E).
3. Si on assimile l'œil à une lentille convergente associée à un écran (rétine) placé à une distance
fixe derrière, quelle est la taille moyenne d'un récepteur de la rétine ?
EXERCICE 8 - Loupe et oculaire (✯✯)
1. Bob utilise une lentille mince convergente de focale comme loupe. Son œil,
emmétrope (PP à la distance ), est au foyer image de la lentille. Dans ces conditions, il observe
un objet AB de hauteur 5,0 mm, placé au foyer objet.
Déterminer le grossissement commercial de cette loupe, défini comme le rapport entre l'angle
sous lequel on voit l'image à l'infini de l'objet à travers la loupe, et l'angle sous lequel on verrait ce
même objet à l'œil nu à la distance minimale de vision distincte .
2. Un oculaire est constitué de deux lentilles et identiques à la lentille précédente, et
séparées par une distance .
2.1. Déterminer les foyers principaux et de ce système.
2.2. Bob observe l'objet précédent, placé à 0,75 cm devant O1, son œil étant placé en F'.
Déterminer le grossissement commercial de ce système.
EXERCICE 9 - Lunette de Galilée (✯✯)
La lunette de Galilée est la lunette la plus simple qui permette d'observer des objets terrestres,
c'est-à-dire sans les renverser. Comme la lunette astronomique (voir TP 2), il s'agit d'un système afocal. On
modélise l'objectif par une lentille "de vergence et l'oculaire par une lentille de
vergence .
1. Déterminer la nature des deux lentilles et les valeurs de leurs distances focales images.
2. Déterminer la distance .
3. Calculer le grossissement en fonction des distances focales et .
αmin = 3,0.10−4rad
d= 2,0 mm
L= 20 mm
f′ = 3,0 cm
dm= 25 cm
α′
α
dm
L1
L2
O1O2= 2,0 cm
F
F′
L1
V1= + 5,0 δ
L2
V2=−20 δ
d=O1O2
f′
1
f′
2
TSI 1 - TD Lentilles minces
Page sur 4 6

4. Un astronome amateur utilise cette lunette, normalement adaptée à la vision d'objet terrestres,
pour observer deux cratères lunaires": Copernic (de diamètre 96 km) et Clavius (de diamètre 240 km).
4.1. L'astronome voit-il ces cratères à l'œil nu"? À l'aide de la lunette"?
Données!: distance Terre-Lune dTL = 3,8.105 km ; acuité visuelle .
4.2. La planète Vénus occultera Jupiter le 22 novembre 2065. Notre astronome amateur
(qui sera certainement confirmé) pourra-t-il observer à l'œil nu ou à l'aide de sa lunette le disque jovien
occulté par Vénus"?
Données supplémentaires!: diamètre de Vénus DV = 12150 km; distance Terre-Vénus
dTV!=!4,5.107 km ; diamètre de Jupiter DJ = 145800 km ; distance Terre-Jupiter dTJ = 6,3.108 km.
EXERCICE 10 - Nearsighted person (✯✯, ")
A nearsighted person is one whose eyes focus light too strongly, and who is therefore unable to
relax the lens inside her eye sufficiently to form an image on her retina of an object that is too far away.
1. Draw a ray diagram showing what happens when the person tries, with uncorrected vision, to
focus at infinity.
2. What type of lenses do her glasses have? Explain.
3. Draw a ray diagram showing what happens when she wears glasses. Locate both the image
formed by the glasses and the final image.
EXERCICE 11 - Microscope (✯✯✯)
Un microscope optique porte les indications suivantes : ×40 sur son objectif"; ×10 sur l'oculaire. La
notice constructeur précise": intervalle optique . Le microscope sera modélisé par deux lentilles
minces convergentes, l'objectif (de diamètre ) et l'oculaire . Il est réglé pour donner une
image à l'infini d'un objet réel , perpendiculaire à l'axe optique, étant placé sur l'axe, légèrement en
avant du foyer objet de l'objectif. Cette image est observée par un oeil emmétrope placé au voisinage du
foyer image de l'oculaire. L'œil nu voit nettement des objets situés entre la distance et
l'infini.
1. Faire un schéma du dispositif (sans respecter l'échelle), et tracer soigneusement la marche de
deux rayons lumineux issus du point de l'objet , l'un émis parallèlement à l'axe optique, l'autre
passant par (foyer objet de , de centre optique ).
αmin = 3,0.10−4rad
Δ= 16 cm
L1
d= 7,0 mm
L2
A B
A
F′
2
dm= 25 cm
B
A B
F1
L1
O1
TSI 1 - TD Lentilles minces
Page sur 5 6
Approfondissement
2. L'indication portée sur l'oculaire (×10) est son grossissement commercial, c'est-à-dire le rapport
de l'angle sous lequel on voit l'image à l'infini d'un objet à travers l'oculaire seul et de l'angle sous lequel
on voit ce même objet à l'œil nu lorsqu'il est situé à la distance minimale de vision distincte. On notera ce
grossissement . Déterminer la distance focale image de l'oculaire.
3. L'intervalle optique est la distance . La valeur absolue du grandissement de l'objet par
l'objectif est (c'est l'indication ×40). Calculer la distance focale image de l'objectif. Calculer la
distance permettant de positionner l'objet.
4. Calculer le grossissement commercial de ce microscope.
5. On appelle cercle oculaire l'image de la monture de l'objectif à travers l'oculaire. Déterminer sa
position par rapport à (centre optique de l'oculaire) et son diamètre. Quel est l'intérêt de placer l'œil
dans le plan du cercle oculaire"? Commenter la valeur trouvée pour son diamètre.
G2= 10
f′
2
F′
1F2
A B
γ1= 40
f′
1
O1A
G
O2
TSI 1 - TD Lentilles minces
Page sur 6 6
Réponses aux exercices d’échauffement
Exercice 1
Exercice 2 et 3
1.1. et 1.2. Utiliser la simulation disponible sur le site de la classe.
1.3. Voir cours
2. Utiliser la simulation disponible sur le site de la classe.
F’
F
6.