CPGE-TSI-3 2022-2023
Devoir libre n° 2
Problème 1: Lunette de Galilée (CCP MP 2007).
En 1610, Galilée témoigne de ses travaux concernant la lunette qui portera bientôt son nom : Je me suis mis à
penser aux moyens de fabriquer l’instrument. J’y parvins si parfaitement que j’en construisis un, formé d’un
tube de fer, extérieurement recouvert d’un drap cramoisi et long d’environ trois quarts de coudée, il comprenait
deux lentilles de la grandeur d’un écu à chaque extrémité, l’une plan concave, contre laquelle on plaçait l’œil,
l’autre plan convexe...
Quel spectacle magnifique et passionnant que de voir le corps lunaire, éloigné de nous de presque soixante
rayons terrestres, rapproché au point de nous sembler éloigné seulement de deux rayons : son diamètre nous
apparaît ainsi trente fois plus grand... qu’à l’œil nu....
La coudée est une unité de mesure correspondant à 50 cm.
1. Quelle est la nature des lentilles utilisées par Galilée ?
2. La lunette est réglée de façon à donner d’une étoile (objet à l’infini) une image à l’infini ce qui permet à
l’observateur d’éviter toute fatigue puisqu’il voit sans accommodation. Dans ces conditions, la lunette est dite
afocale.
a) Préciser et justifier la position des foyers dans une lunette afocale.
b) Réaliser un schéma, sans respecter les échelles, montrant le devenir d’un rayon incident faisant un angle α
avec l’axe optique et émergeant sous un angle α’ dans les conditions de Gauss.
c) Déterminer l’expression du grossissement G = 𝛂’
𝛂 de la lunette en fonction de 𝐟𝟏
′, distance focale de
l’objectif et 𝐟𝟐
′, distance focale de l’oculaire.
d) Montrer, en utilisant le texte de Galilée, que le grossissement de sa lunette est environ égal à 30. En déduire
les valeurs approximatives des distances focales et des vergences de chacune des lentilles utilisées.
3. Du haut du Campanile de Venise, les sénateurs vénitiens invités par Galilée, observent avec cette lunette, en
direction de Murano à 2,5 kilomètres de là. Ils distinguent avec enthousiasme le mouvement des gens !
a) Sous quel angle les personnes de 1,7 m sont-elles observables à travers l’instrument?
b) À quelle distance les sénateurs ont-ils, dans ces conditions, l’impression de voir les habitants de Murano, si
on se réfère aux textes de Galilée reportés au début du problème ?
4. Un astronome amateur utilise cette lunette normalement adaptée à la vision d’objets terrestres pour observer
deux cratères lunaires : Copernic de diamètre dCop = 96 km et Clavius de diamètre
dCla = 240 km. On rappelle que la distance Terre-Lune est DTL = 384 000 km.
a) L’astronome voit-il ces deux cratères lunaires à l’œil nu ? On donne l’acuité visuelle 3.10−4 rad. Même
question à l’aide de cette lunette. Justifier les réponses.
b) La planète Vénus dont le diamètre vaut dVen = 12 150 km occultera Jupiter de diamètre
dJup = 145 800 km le 22 novembre 2065. L’astronome amateur (qui sera certainement confirmé) pourra-t-il
observer à l’œil nu ou à l’aide de sa lunette le disque jovien occulté par Vénus ? Dans cette configuration, la

CPGE-TSI-3 2022-2023
distance Terre - Vénus sera DTV = 45.106 km. On précise que la distance Terre - Jupiter DTJ varie entre 588 et
968.106 km.
Problème 2: Modèle simplifié de l’œil pour la vision de près.
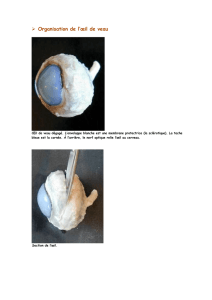
L’œil humain a sensiblement la forme d’une sphère limitée par une membrane (la sclérotique) qui est
transparente à l’avant de l’œil et forme la cornée (figure 1). L’intérieur du globe oculaire est divisé en deux
parties séparées par le cristallin qui est une lentille convergente. Cette lentille est élastique et ses rayons de
courbure varient lorsque l’œil accommode, c’est-à-dire quand il passe de la vision de loin à la vision de près.
La partie antérieure entre la cornée et le cristallin est remplie d’un liquide appelé humeur aqueuse. L’iris permet
à l’œil de diaphragmer et définit la pupille. La partie postérieure du cristallin est formée du corps vitré. La rétine
qui sert de détecteur est tapissée de cellules de deux types différents, les cônes et les bâtonnets qui transforment
l’excitation lumineuse en influx nerveux. La fovéa, partie de la rétine située sur l’axe optique de l’œil, est la
partie la plus sensible de la rétine.
Figure 1 : coupe de l’œil humain.
Modèle simplifié de l’œil pour la vision de près.
Pour la vision de près, on peut assimiler l’œil à une lentille mince (L) biconvexe, convergente, plongée dans
l’air d’indice 1. Tous les rayons lumineux seront considérés comme étant paraxiaux. S est le centre optique de
la lentille, Fo son foyer principal objet, Fi son foyer principal image, V sa vergence et fi sa distance focale image.
La rétine, centrée au point R, est située à une distance du cristallin anatomiquement invariable :
la distance SR = 16,7 mm reste fixe quelle que soit l’accommodation. L’œil normal (emmétrope) permet de voir
des objets situés devant lui depuis la distance dmin = 25cm (distance minimale de vision distincte) jusqu’à la
distance dmax infinie (distance maximale de vision distincte). Pour cela, l’œil accommode, c'est-à-dire que les
rayons de courbure de la lentille biconvexe se modifient sous l’effet des muscles ciliaires. On se place dans le
cas de la vision de près quand l’œil accommode au maximum. Si l’image se forme sur la rétine au niveau de la
fovéa, l’œil peut distinguer deux points proches suffisamment contrastés si leur distance angulaire est supérieure
à ε= 4.10-4rad. Cette limite de résolution augmente fortement en vision périphérique.

CPGE-TSI-3 2022-2023
1. On note po=𝑆𝐴o la mesure algébrique repérant la position d’un objet lumineux AoBo perpendiculaire à l’axe
optique et dont l’image se forme sur la rétine. La position de l’image est repérée par la grandeur algébrique
p=𝑆𝐴i.
1.a Donner la relation entre po, pi et la vergence V de la lentille (L). Quel nom porte cette relation ? Donner la
dimension de la vergence V et son unité en fonction des unités de base du Système International.
1.b Calculer la valeur Vmax de V quand l’œil emmétrope regarde un objet situé à la distance minimale de vision
distincte dmin.
1.c Calculer la valeur Vmin de V dans le cas où ce même œil emmétrope regarde un objet placé cette fois à la
distance maximale de vision distincte dmax.
1.d La variation de la vergence de l’œil A=Vmax-Vmin est appelée l’amplitude d’accommodation. Calculer A dans
le cas de l’œil emmétrope.
2. Avec l’âge, l’amplitude d’accommodation se réduit. Cette diminution physiologique porte le nom de
presbytie. En pratique, un individu devient presbyte quand il doit éloigner son journal de plus de 35 cm de son
œil pour lire. Dans ce cas, la distance minimale de vision distincte augmente (d’min=35cm) et d’max=dmax reste
inchangé.
2.a Déterminer l’amplitude d’accommodation de l’œil emmétrope d’un individu devenu presbyte.
2.b Quelle est la taille AoBo minimale des caractères du journal placé à d’min = 35cm, que peut lire cet individu
devenu presbyte ?
2.c Quelle serait la taille AoBo minimale des caractères si la presbytie de l’individu augmentait de telle façon
qu’il doive placer le journal à 1 m de son œil ? Conclure.
3. Une personne voit nettement un point à l’infini sans accommoder mais ne peut voir un point situé à moins de
1 m en accommodant au maximum. Pour pouvoir lire confortablement un journal placé à 25 cm devant lui, il
porte des lunettes dont chaque verre (assimilé à une lentille mince convergente (LL) de vergence VL et de centre
optique SL) est placé 2 cm devant le centre optique de l’œil (figure 2). Dans ces conditions, il n’accommode
pas.
Figure 2 : lentille correctrice placée devant l’œil pour la vision de près.
En reprenant le schéma de la figure 2, représenter deux rayons issus de Bo qui atteignent la rétine. Les
échelles peuvent ne pas être respectées mais vous justifierez votre construction géométrique.

CPGE-TSI-3 2022-2023
Chimie: obtention industrielle du zinc :
Dans la nature, le zinc (Zn) se rencontre dans la blende, minerai cons titué essentiellement de sulfure de zinc
solide ZnS(s).
Pour récupérer le métal zinc Zn(s), dont la principale utilisation est l’élaboration de l’acier zingué, la blende
subit de multiples transformations physico-chimiques. La blende est ainsi transformée en calcine, lors d’une
étape appelée « grillage ». Puis la calcine est attaquée par une solution d’acide sulfurique, lors d’une étape
appelée « lixiviation ». Après cette étape de lixiviation, on obtient une solution très acide contenant des ions
zinc Zn2+, mais également un grand nombre d’impuretés, parmi lesquelles figurent les ions fer Fe3+ et les ions
cuivre Cu2+.
On modélise la solution obtenue après la lixiviation par un mélange acide contenant les ions cuivre à la
concentration [Cu2+] = 3,0.10-2 mol.L-1, les ions fer à la concentration [Fe2+] = 3,0.10-2 mol.L-1 et les ions zinc à
la concentration [Zn2+] = 0,90 mol.L-1
On rajoute de la soude dans la solution
1. Calculer le pH de la solution lorsque le précipité d’hydroxyde de fer III apparait.
2. Calculer le pH de la solution lorsque le précipité d’hydroxyde de cuivre apparait.
3. Calculer le pH de la solution lorsque le précipité d’hydroxyde de zinc apparait.
4. Afin de ne pas faire précipiter les ions Zn2+, on ajuste le pH de la solution à 5 :
4.a. Calculer la concentration des ions hydroxyde dans le mélange lorsque le pH est de 5
4.b. Calculer la concentration des ions fer 3 dans la solution ; peut-on considérer qu’ils ont entièrement
précipité?
4.c. Calculer la concentration des ions cuivre dans la solution ; peut-on considérer qu’ils ont entièrement
précipité ?
4.d. Quelles sont alors les dernières étapes qui permettent d’obtenir du zinc pur ?
Constantes d’équilibre de dissolution à 20°C
De l’hydroxyde de fer III Fe(OH)3 : Ks = 2,5.10-38
De l’hydroxyde de cuivre Cu(OH)2 : Ks = 2,0.10-20
De l’hydroxyde de zinc Zn(OH)2 : Ks = 6,7.10-18
1
/
4
100%