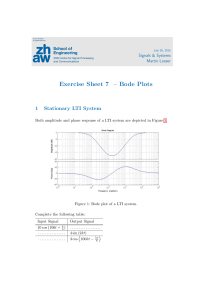
Grade 11 Trigonometry Workbook: Definitions, Equations, Exercises

TRIGONOMETRY
here
Tara Conradie
Grade 11
23 July 2022

TRIGONOMETRY
NB - make sure your calculator is on ‘DEG’
1. DEFINITIONS, IDENTITIES & RULES:
1.1 Definitions:
For any size  :
⚫   
⚫   
⚫   
1.2 Identities:
⚫   
cos
⚫ sin cos  
⚫ 
⚫ sin2  cos
⚫ cos2  sin
1.3  Rule:
1) Determine the quadrant
2) Use CAST diagram to determine the sign
3) Keep the same ratio (sin, cos or tan), but
possibly change the sign.
e.g.  
because  is in the 3rd
quadrant, where sine is negative
1.4  Rule:
⚫   ⚫  
⚫    ⚫  
⚫

2. SPECIAL ANGLES:
2.1 Special triangles:
Know the 45/30/60 ratios without a
calculator.
Use calculator for 0/90/180/270/360
⚫  
⚫  
⚫   
⚫  
 ⚫  
⚫   
 ⚫   
⚫   ⚫  
2.2 Combined with and rules:
ALWAYS first reduce to an acute angle.
e.g.  

3. USING SKETCHES:
3.1 If    , use a sketch (and not a
calculator) to find  if
⚫ Must be quadrant 3 where cos is negative.
⚫ Use Pythagoras to calculate .
⚫ Watch out for the sign.
3.2 If  
 , write sin in terms
of  .
⚫ Draw a right-angled triangle and fill in
 and  on the opposite and adjacent
sides.
⚫ Use Pythagoras to calculate the 3rd side.
⚫ sin2 
4. TRIG EQUATIONS:
4.1
⚫ Equations must be manipulated to give:
⚫ Watch out for   the number   for
sin / cos 
⚫ First find the help-angle:
⚫ Then use CAST-diagram to determine
quadrants where positive or negative.
⚫ sin / cos /  a number
⚫ SHIFT-button (don’t push minus)
4.2
⚫ General solution:
⚫ Interval given:
⚫ sin / cos :   
⚫ tan :   
⚫ Find all angles in interval by substituting
   etc
⚫
Y
X
⚫    , therefore   

4.3
⚫   
⚫   
⚫ Divide by  to get 
⚫ Use the  rule to change sin ↔ cos
4.4 Factorising:
eg.     
eg. sin2 cos  
eg. sin  cos2  
eg.  cos    
⚫ Common factor
⚫ Difference of squares
⚫ Trinomial
⚫ Grouping
⚫ Sum & Difference of cubes