cours-douvrages-dart-t2-2008

_______________________________________________________________________
ENIT, BP 37-1002 Tunis-Le Belvédère, Tunisie Télécopie:216-71-872-729
E-mail : mongi.benouezdo[email protected]
par
Mongi BEN OUÉZDOU
Mise à jour : Octobre 2008
École Nationale d’Ingénieurs de Tunis
COURS D’OUVRAGES D’ART
Tome 2 : Dimensionnement

Préface
Ce document traite le dimensionnement des ouvrages. Il est le fruit de 16 ans
d’enseignement du module d’ouvrages d’art dans des écoles d’ingénieurs. Il
présente le dimensionnement des tabliers des ponts à poutres. Le choix de ce type
d’ouvrages est basé sur deux critères :
¾Dans la plus part des cas, cet ouvrage est à travées indépendantes. Son
calcul n’est pas « très compliqué » par rapport à celui des ouvrages continus. Dans
la pratique, son étude se fait manuellement. Alors que pour les autres types
d’ouvrages (ponts dalles, portiques, …), on fait recours au calcul automatique par le
SETRA* ou par des codes d’éléments finis, tels que Robot, SAP et Effel.
¾Grâce à l’étude de ce type de ponts, on peut étudier les différents cas
d’ouvrages tels que les ponts dalles et les portiques. C’est les lignes d’influences
qui peuvent changer pour ces cas hyperstatiques, mais la méthode de Guyon-
Massonnet reste valable.
Ce polycopié débute par un chapitre de rappel sur les lignes d’influences, qui va
servir pour le calcul des poutres principales présenté plus tard (troisième chapitre).
Ensuite, le chapitre deux présente les règlements des charges pour les ponts-routes
et pour les ponts rails (règlements français employés en Tunisie). Le chapitre trois
comporte les détails de calcul des sollicitations poutres principales dans le sens
longitudinal avec un annexe de calcul de la répartition transversale par la méthode
de Guyon-Massonnet et un annexe des tables de Guyon-Massonnet. Les détails de
calcul du ferraillage n’ont pas été traités ici, puisque les poutres sont calculées en
flexion simple, sujet traité dans le cours de béton armé.
Ensuite, nous présentons un chapitre spécifié au calcul des entretoises d’appui,
suivi d’un chapitre qui traite en détail le calcul des hourdis** des ponts à poutres. En
effet, ce cinquième chapitre présente le calcul à la flexion locale par les abaques de
Mougin (présenté en annexe 1) et le calcul de la flexion globale par la méthode de
Guyon-Massonnet dont les tableaux sont présentés en annexe 2. Ce même chapitre
est récapitulé par la flexion totale et suivi par les particularités du ferraillage du
hourdis (calcul aussi à la flexion simple).
Enfin, un dernier chapitre, en cours d’élaboration, présente le principe de calcul
des appareils d’appui et des appuis. C’est un chapitre qui reste à compléter, ainsi
que l’étude des fondations.
* SETRA : Service d’Etudes Techniques des Routes et des Autoroutes, France.
** Hourdis: Dalle pleine du pont à poutres (plus mince que pour les ponts dalles).
Mongi Ben Ouézdou
Maître de Conférences à l’ENIT
Tunis, le 09 Octobre 2008

M.Ben Ouézdou Cours d’Ouvrages d’Art, Tome 2 : Dimensionnement
Chap 1: Les lignes d’influences. 1
Chap 2 : Les règlements de charges sur les ponts. 10
ETUDE DES PONTS A POUTRES A TRAVEES INDEPENDANTES
Chap 3 : Calcul des poutres principales 35
Annexe au chapitre 3 : Méthode de Guyon-Massonnet 52
Chap 4 : Etudes des entretoises d’about. 95
Chap 5 : Calcul des hourdis 99
Annexe 1 au Chap 5 : Abaques de Mougin. 135
Annexe 2 au Chap 5: Tableaux de Guyon-Massonnet 150
Chap 6 : Quelques données sur le calcul des apppuis 155

M.Ben Ouézdou Chap 1, page 1
P = 1
L
x
Chapitre 1
1-1 Introduction p 1
1-2 Lignes d’influences des poutres sur appuis simples p 1
1-3 Emploi des lignes d’influences p 3
1-4 Lignes d’influences d’autres poutres isostatiques p 4
1-5 Lignes d’influences des poutres continues p 8
1-1- Introduction
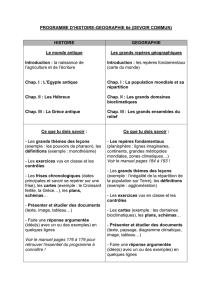
Les lignes d’influences sont obtenues pour une section donnée x. Dans le cas des poutres, ces
lignes d’influences sont déterminées pour les moments fléchissants et les efforts tranchants. Ils sont
obtenus en faisant un balayage d’une charge unitaire (P=1) le long de la poutre et en cherchant le
moment fléchissant ou l’effort tranchant dans la section x considérée.
Figure 1 : Section x pour une ligne d’influence.
Donc une ligne d’influence est toujours liée avec une section donnée (x). On écrit pour les lignes
d’influences des moments fléchissants : Li "Mx" et ceux des efforts tranchants : Li "Tx".
1-2- Lignes d’influences des poutres sur appuis simples
Les lignes d’influences des moments fléchissants et des efforts tranchants sont présentées dans
la Figure 2 ci-après. Pour les moments fléchissants, la ligne d’influence d’une poutre sur appui simple
est une ligne brisée dont le sommet, y, est :
L
xLx
y
Ainsi, les valeurs sont positives et de même signe. Pour les efforts tranchants, la ligne d’influence est
formée par deux parties (Figure 2): une partie positive d’extrémité, y’, tel que :
¸
¹
·
¨
©
§
 L
x
1'y .
Et une partie négative d’extrémité : ¸
¹
·
¨
©
§
L
x
LES LIGNES D’INFLUENCUES

M.Ben Ouézdou Chap 1, page 2
L
x
L
xLx
y
Li “Mx”
AB
1
L
x
1'y 
L
x
Li “Tx”
L
x = L/2
4
L
y
Li “ML/2”
AB
1
Li “T0”
(L-x)
x1x2
y1y2
x = 2
L y = L4
L2
x = 0 y = 1 – 0 = 1
Figure 2 : Lignes d’influences des moments fléchissants et des efforts tranchants dans une section x.
Les valeurs des ordonnées y1 ou y2 sont retrouvées à partir de la règle des triangles semblables (ou
Thalès). Ainsi, connaissant x, y, x1 on peut retrouver y1, c.à.d.,
¸
¹
·
¨
©
§
x
x
.yy 1
1 avec y = L
)xL(x 
De la même manière, en connaissant (L-x), y, et x2 on peut retrouver y2.
¸
¹
·
¨
©
§
xL
x
.yy 2
2
Pour les valeurs des ordonnées intermédiaires des lignes d’influences des efforts tranchants, nous
procédons de la même manière.
Application des lignes d’influences : Lignes d’influence des moments fléchissants à x = L/2 (au milieu
de la travée) et les lignes d’influences des efforts tranchants à x = 0 (Réaction d’appui).
Figue 3 : Lignes d’influences des moments fléchissants à x= L/2
et lignes d’influences des efforts tranchants à la section x=0.
1