titre clair

CIRCUITS MAGNETIQUES
1
CIRCUITS MAGNETIQUES

CIRCUITS MAGNETIQUES
2
i i
Φ Ψ
f
Ψ
M
1
1 2
I CIRCUITS MAGNETIQUES EN COURANT CONTINU
Introduction
Dans les machines électriques l’utilisation des champs électriques a imposé la réalisation du circuit
magnétique ayant des formes adaptées.
Un circuit magnétique est un ensemble de milieu comprenant essentiellement des substances
ferromagnétique (Fer, Cobalt, Nickel….) capable de prendre une forte aimantation même à l’absence
de champ magnétique .
L'importance des matériaux ferromagnétique en électrotechnique provient du fait qu'ils sont
capables de canaliser et de capter en leur sein le flux de toute induction due à des courants situés
dans leur voisinage et, en particulier, enroulés autour d'eux.
I °/Excitation magnétique en un point P donné
Considérons un point M situé à l’intérieur d’un bobinage torique parcouru par un
courant .L’excitation magnétique en ce point est une grandeur vectorielle.
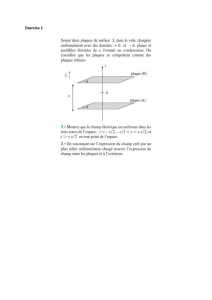
Figure 1
Canalisation du flux
Considérons un circuit électrique bobiné dans l'air et le même circuit bobiné autour d'un noyau
ferromagnétique (Figure1). Dans les deux cas, les excitations magnétiques aux points M 1 et M 2 sont
du même ordre de grandeur. Elles dépendent des paramètres géométriques de la bobine pour le
circuit n°1 et en plus de la longueur du noyau dans le circuit n°2.
Considérons le champ magnétique :
Au point M 1 , dans l'air, il vaut :
0
B H
µ
= avec µo : Perméabilité absolue de l’air et vaut 4π S.I ;

CIRCUITS MAGNETIQUES
3
Mais en M 2 , il vaut
0r
B H
µ µ
= , c'est-à-dire que le champ est µ r fois plus grand. Etant donné que µ r
atteint des valeurs comprises couramment entre 1000 et 5000, on voit que le champ B dans le matériau
ferromagnétique sera 1000 à 5000 fois plus grand que dans l'air. On pourra considérer que la majeure
partie du flux est canalisée dans le noyau.
REMARQUE :
=
En conclusion on a avec µ : Perméabilité magnétique absolue
3°) Le théorème d’Ampère
La circulation du vecteur excitation magnétique
H
uur
le long d'une ligne d'induction Γ fermée
entourant un circuit C parcouru par un courant i est égale au produit du courant i par le nombre de
fois que cette ligne Γ traverse le circuit C.
Ou encore : la circulation du vecteur excitation magnétique le long d'un contour fermé est égal à la
somme algébrique des intensités électriques traversant une surface quelconque supportée par ce
contour.
H dl ni
Γ
⋅ =
∫
uur uur
La quantité qui intervient au second membre s'appelle la "force magnétomotrice" du circuit :
F.M.M. = Ni = F en unité SI, une F.M.M. se mesure en "ampère-tour", symbole At, ou plus simplement
en ampère A.
II °/ Modèle linéaire du circuit magnétique
Le circuit magnétique considéré est réalisé dans un matériau ferromagnétique. La saturation est
négligée : la perméabilité µ est constante.
En tout point B=µ H avec µ = Cte.
1°) Circuit magnétique sans entrefer
Le circuit est de section constante et ne présente pas de fuite magnétique. En appliquant le théorème
d’ampère à ce circuit magnétique (ligne de champ de longueur l)
=Hl=Ni
Soit le flux a travers le tube d’induction. Considérons constante on a =BS= µ.H.S => H=

CIRCUITS MAGNETIQUES
4
i
f
H
uuur
l
n spires
e
e
H
uur
µ
r
Γ
On sait que: Hl=Ni => =Ni Posons R= avec R=reluctance du circuit magnétique et s’exprime
en
On obtient : R. φ=Ni c’est La relation d’Hopkinson avec ℰ =Ni s’exprime en Ampère(A)
2°) Circuit magnétique avec entrefer
Le circuit magnétique est forme de 2 tronçons homogènes: l’un constitue de matériau
ferromagnétique et l’autre de l’entrefer suppose d’épaisseur e (faible).
Le flux φ a la même valeur pour toute section magnétique. Le champ magnétique B a la même valeur
dans tout le matériau et dans l’air.
La circulation de l’excitation magnétique H le long de la
ligne moyenne du champ est égale:
H f (l-e)+H e el sensiblement égal a H f l+H e e avec (l >>e)
Le théorème d’ampère s’écrit alors:
H f l+H e e=Ni
avec H f à l'intérieur du fer et H e dans l'entrefer
On obtient la reluctance du circuit magnétique qui s’écrit:
R=
CONCLUSION
Créer un entrefer dans un circuit magnétique augmente la reluctance de ce circuit.

CIRCUITS MAGNETIQUES
5
II
CIRCUITS MAGNETIQUES EN ALTERNATIF
I°/ Bobine soumise à une tension sinusoïdale
1°) Equation générale
Déterminons l’équation générale exprimant la tension d’entrée u aux bornes des spires enlaçant un
noyau de fer en fonction de : i , et f (grandeurs électromagnétiques)
Soit t le flux total à l’intérieur des spires qui se sépare pour
circuler dans deux matériaux différents : le flux principal qui
circule dans le noyau de fer et le flux f qui circule dans l’air
ambiant ( f à une valeur très faible). On a :
u =ri+n => u =ri+n => u=ri+n
Or = l f = > u=ri+ + l f avec l f : inductance de fuite car elle relative aux flux de fuite .
2°) Formule de BOUCHEROT
Par hypothèses on néglige : l’influence la résistance r des enroulements (ri=o) ainsi que l’influence de
l’inductance de fuite l (l f =0).Ce qui conduit à la relation suivante : => u =
La tension d’entrée u est sinusoïdale u= U eff
=> )
On constate que :
• le flux est sinusoïdal
• est en quadrature arrière par rapport à u
•
On en déduit que : max = , => U = et ߱=2πf => U =
U=4,44 max SNf
avec
max
=B
max
S