IPT SPE TP3

SPE - 2021/2022 TP 3 : Labyrinthes parfaits Informatique
Un labyrinthe est dit parfait s’il satisfait la
propriété suivante : “Pour tout couple de cases, il existe
un unique chemin les reliant.”
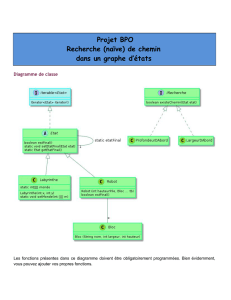
On modélisera un labyrinthe comme un tableau à
double entrée (liste de listes) d’objets appartenant à la
classe Case. Chaque instance de Case est définie par cinq
attributs booléens :
•les attributs N, S, E et W indiquent la présence de
murs au nord, sud, est et ouest de la case considérée,
•l’attribut etat indique que la case a déjà été visitée.
Vous trouverez sur la page web du cours un fichier
laby.py contenant un squelette de code que vous devez
télécharger et ensuite compléter.
1class Case:
2def __init__(self):
3self.N=True
4self.W=True
5self.S=True
6self.E=True
7self.etat =False # indique si la case a été visitée
8
9class Labyrinthe:
10 def __init__(self, larg, haut):
11 self.haut =haut
12 self.larg =larg
13 self.tab =[[Case() for jin range(haut)] for iin range(larg)]
La classe Labyrinthe est construite de manière à ce que, pour toute instance maze de la classe
Labyrinthe,maze.tab[x][y] désigne la case du labyrinthe dont le coin inférieur gauche a pour
coordonnées (x, y).
Exercice 1 : Tester les commandes suivants :
1new =Labyrinthe(25,30)
2new.show()
1. Le labyrinthe généré vous semble-t-il parfait ?
2. Quelle est sa forme ?
3. Compléter la définition de la classe Labyrinthe par une fonction clean qui réinitialise l’attribut etat
de chaque case du labyrinthe à False.
Construction d’un labyrinthe parfait
Il existe plusieurs types d’algorithmes générant des labyrinthes parfaits. On s’intéresse ici à un
algorithme de construction par exploration exhaustive du labyrinthe. L’algorithme est décrit ci-dessous.
•On crée un labyrinthe dont tous les murs sont fermés et dont aucune case n’a été visitée,
•On crée une pile (initialement vide) destinée à contenir l’ensemble des cases à traiter par l’algorithme.
•On choisit une case au hasard dans le labyrinthe. On modifie alors l’état de cette case pour indiquer
qu’elle est visitée et on l’empile dans la pile des cases à traiter.
•Tant que la pile est non vide, on répète la suite des instructions ci-dessous.
A. Lick 1 Janson de Sailly

SPE - 2021/2022 TP 3 : Labyrinthes parfaits Informatique
•On visite la case au sommet de la pile (sans la dépiler).
•On détermine la liste de ses cases adjacentes non visitées.
•Si la case n’a aucune voisine non visitée, on la dépile de la pile des cases à traiter.
•Sinon, on en choisit une au hasard, on modifie son état pour indiquer qu’elle est désormais
visitée, on “casse” le mur entre les deux cases et on empile la nouvelle case dans la pile des
cases à traiter.
Exercice 2 : Écrire une fonction creationLabyrinthe qui génère (renvoie) selon l’algorithme précédent
une instance de la classe Labyrinthe (i.e. un labyrinthe parfait), dont la taille (largeur et hauteur) sont
fournis en argument d’entrée.
On pourra utiliser la fonction random.randint(a,b) qui renvoie un entier choisi aléatoirement entre
aet binclus. Vous prendrez des initiatives en introduisant des fonctions auxiliaires (par exemple pour
casser un mur ou déterminer la liste des cases adjacentes).
Tester votre fonction avec le code ci-dessous.
1maze =creationLabyrinthe(30 ,30)
2maze.show()
Exercice 3 (Si vous êtes en avance) :
•Démontrer que l’algorithme précédent génère des labyrinthes parfaits.
•Combien de murs internes a-t-on cassé ? Combien de murs internes reste-t-il ?
Recherche du chemin solution
On décide (arbitrairement) de fixer l’entrée et la sortie du labyrinthe aux coins respectivement en bas
à gauche et en haut à droite 1.
On présente ici un algorithme de recherche du chemin solution par backtracking (retour en arrière).
Le principe de cet algorithme est simple 2: on suit un chemin jusqu’à la solution ou une impasse et, dans
le deuxième cas, on revient sur ses pas jusqu’à la dernière intersection. Les étapes de cet algorithme de
recherche sont similaires à celles de l’algorithme de construction de labyrinthes parfaits précédemment
décrit.
•On crée une pile (initialement vide) des cases visitées.
•On empile les coordonnées de l’entrée du labyrinthe, et on marque la case comme visitée.
•Tant que la sortie n’a pas été trouvée, on visite le sommet de la pile (sans le dépiler).
•On le marque comme visité.
•Si c’est la sortie, on sort de la boucle et on renvoie le contenu de la pile.
•Sinon, on teste une par une toutes les cases adjacentes accessibles : si l’une d’entre elle n’a pas
encore été visitée, on l’empile dans la pile des cases visitées. Dans le cas contraire, on est au
bout d’une impasse ; on dépile donc la dernière case visitée.
Cet algorithme d’exploration s’appelle algorithme de parcours en profondeur.
Exercice 4 :
1. Écrire une fonction depthFirstSearch qui parcourt en profondeur le labyrinthe selon l’algorithme
présenté ci-dessus et qui renvoie le chemin solution (sous forme de liste des coordonnées des cases à
visiter).
2. Compléter la définition de la classe Labyrinthe par une fonction solution qui affiche (dans une
autre couleur que celle utilisée pour tracer le labyrinthe) le chemin solution calculé par la fonction
précédente.
1. Si maze est une instance de Labyrinthe, l’entrée est sur la case maze.tab[0][0] et la sortie sur
maze.tab[maze.larg-1][maze.haut-1].
2. C’est la méthode du fil d’Ariane qui permit à Thésée de sortir du Labyrinthe (créé par Dédale) dans lequel le roi
Minos a enfermé le Minautore.
A. Lick 2 Janson de Sailly