4-transformateur Monophasé

Prof : Z. ERRACHIDI
Lycée Technique AL khawarizmi
Unité : A.D.C
20……/20……
Classe : 2ème BAC - STE
Fonction Alimenter : Transformateurs monophasés
Cours N° : 4
P : 1
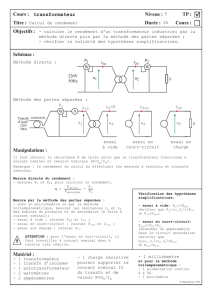
I. Introduction :
1) Rôle :
Le transformateur est un convertisseur statique « alternatif-alternatif » qui permet de modifier la valeur
efficace d’une tension alternative en maintenant la fréquence et la forme de l’onde inchangées.
2) Symbole :
3) Principe de fonctionnement :
Il est constitué de 2 enroulements placés sur un circuit magnétique fermé :
➢ Le primaire est alimenté par le
réseau et se comporte comme un récepteur.
Il crée un champ et un flux magnétique
(Φ(t) alternatif) dans le circuit magnétique
feuilleté.
➢ Le secondaire est soumis à la
variation de ce flux, il est le siège d'une
f.é.m. induite due à la loi de Lenz
(e= -N dΦ/dt) , il se comporte comme un
générateur qui alimente une charge.
Un transformateur qui produit une tension
plus grande est dit élévateur de tension, à
l'inverse il est dit abaisseur de tension.
II. Transformateur parfait :
1) Hypothèses simplificatrices :
Un transformateur est parfait si on néglige :
➢ Les résistances des enroulements ; (r1=0) et (r2=0),
(pas de pertes de joules).
➢ Les inductances de fuite ; (L1 = 0) (L2 = 0)
➢ La réluctance du circuit magnétique. (
f = 0)
➢ Pas de pertes de Fer.
2) Equations électriques :
• A chaque instant, chaque spire est traversée par le même flux magnétique.
Au primaire
Au secondaire
e1 (t) = - N1 
 et v1(t) = - e1(t) = N1 
en complexe : V1 = -E1 = jωN1  (1)
e2(t)= - N2 
 et v2(t) = e2(t)= - N2 
en complexe : V2 = E2 = - jωN2Φ (2)
On obtient alors :
 =-m v1 et v2 sont en opposition de phase
Adapter la tension
Tension d’alimentation
Tension d’utilisation

Prof : Z. ERRACHIDI
Lycée Technique AL khawarizmi
Unité : A.D.C
20……/20……
Classe : 2ème BAC - STE
Fonction Alimenter : Transformateurs monophasés
Cours N° : 4
P : 2
Cette relation indique que les tensions v1 et v2 sont en opposition de phase.
La relation entre les valeurs efficaces V1 et V2 ne tient pas compte du déphasage : 
 =m
m est le rapport de transformation du transformateur.
Formule de Boucherot :
L’équation (1) donne en valeur efficace : V1 = E1 = ω N1 Φ = 2 π f N1 Φ
max /
√ 2 = 4,44 f N1 Φ
max
V1 = 4,44. f. N1.s.Bmax et V2 = 4,44. f .N2 .s.Bmax avec Φ
max = s.Bmax
U, E (valeurs efficaces) en (V),
B : (champ magnétique) en Tesla (T),
s : (section de fer) en (m2)
f : (fréquence) en (Hz).
3) Relations entre les intensités :
Bilan des puissances : P1= P2 (transformateur parfait) soit le rendement est : η = P2/P1
Comme 1 =  2 on a: S1= S2 = U1. I1= U2 .I2 ↔  
NB: Selon la valeur de m, on peut distinguer :
▪ si m>1 V2>V1 et I2<I1 le transformateur est dit élévateur de tension ;
▪ si m<1 V2<V1 et I2>I1 le transformateur est dit abaisseur de tension ;
▪ si m=1 V2=V1 et I2=I1 le transformateur est dit isolateur ;
4) Puissances d’un transformateur Parfait :
On a:  
▪ Puissance apparente : =
1 ×I1 =
×
×
2 = 2 × 2 donc S1=S2
▪ Puissance active : d’après la définition du transformateur parfait P1=P2=
1
×
1= 2
×
2
▪ Puissance réactive :
1 = 1
×
1 = 2
×
2 = 2
▪ Conclusion : Le rendement d’un transformateur parfait est égal à 1 (pas de pertes)
Les puissances absorbées par le primaire seront absorbées par la charge connectée au secondaire.
5) Schéma électrique équivalent et diagramme de Fresnel :
Un transformateur parfait est alimenté au primaire par une tension sinusoïdale u1. Il alimente
une charge Z2, telle que le courant i2 présente un déphasage d’un angle φ2 avec la tension u2.
L’intensité du courant I2 dépend de la charge appliquée au secondaire, il en est de même pour le
facteur de puissance cos φ2. Ces deux grandeurs imposent l’intensité du courant I1 appelé au
primaire, ainsi que le facteur de puissance du primaire cos φ1, sachant que φ1 = φ2.

Prof : Z. ERRACHIDI
Lycée Technique AL khawarizmi
Unité : A.D.C
20……/20……
Classe : 2ème BAC - STE
Fonction Alimenter : Transformateurs monophasés
Cours N° : 4
P : 3
III. Transformateur réel :
En éliminant toutes les hypothèses précédentes :
En réalité : P2 < P1 et le rendement < 1 car : il y’a présence des pertes. Alors dans un
transformateur réel, On tient compte des résistances des enroulements primaires et secondaires R1
et R2 et les inductances de fuites L1 et L2 des bobinages. De Rf et Lm la résistance équivalente
aux pertes fer et l’inductance magnétisante vue du primaire. Le schéma équivalent du
transformateur réel est représenté sur la figure ci-dessous.
1) Bilan des puissances :
P1 et P2 sont des puissances électriques (actives) : P1 = V1 I1 cosφ1 et P2 = V2 I2 cosφ1.
Le rendement du transformateur est :  =
=
Le transformateur réel est un transformateur parfait avec des pertes (Joule, fer), ces pertes ont
deux origines :
➢ Electrique Les pertes Joules (ou pertes cuivre) dans les enroulements : R1 : résistance de
l'enroulement primaire R2 : résistance de l'enroulement secondaire ; Pj = R1 I1 ² + R2 I2 ²
➢ Magnétique (pertes fer) : Pertes par courants de Foucault et Pertes par hystérésis
2) Détermination des pertes et des paramètres du transformateur :
a) Essai avec secondaire à vide :
L’essai à vide permet de mesurer :
✓ Les pertes fer Pfer
✓ Le rapport de transformation m
✓ La branche Magnétisante Rf et Xm
A la tension primaire nominale on place le wattmètre pour mesurer la puissance primaire à vide P10
P1= Pfer + PJ + P2 A vide : P2 = 0 W et PJ = R1 I10 ² + 0 : négligeable car I10 négligeable (I2 nul)
➢
10 = fer + 1 102
Alors : = et =
V1
V20
V1
V2

Prof : Z. ERRACHIDI
Lycée Technique AL khawarizmi
Unité : A.D.C
20……/20……
Classe : 2ème BAC - STE
Fonction Alimenter : Transformateurs monophasés
Cours N° : 4
P : 4
Détermination de Rf et Xm (Branche Magnétisante) :
Détermination de Rf : Pf= P10 = Rf.I10a2 avec I10 =
  Rf=
Détermination de Xm : Q10 = P10 .tgφ0 = Xm I10r2 avec I10 =
  Xm=
Facteur de puissance cos φ10 : P10=V1 I10 cos φ10  cos φ10 = 
b) Essai en court-circuit :
L’essai en court-circuit permet de mesurer :
✓ Les pertes joules Pj
✓ Le rapport de transformation m
On se place à V1cc réduite, de façon à avoir I2cc=I2n (valeur nominale). Le wattmètre mesure P1cc la
puissance absorbée en court-circuit par le transformateur :
➢ P1CC= Pfer + Pj+ P2
En court-circuit : P2= 0 W (car V2 = 0V)
L’essai se fait sous tension primaire réduite (V1cc << V1N). Les pertes fer sont proportionnelles à
V1 ² donc elles sont négligeables. Finalement =
Alors  =  et  =
3) Modèle du transformateur avec l’Hypothèse de Kapp :
L’hypothèse de Kapp consiste à négliger le courant I10 devant les courants I1 et I2 au
fonctionnement nominal. Cela revient à débrancher l’impédance magnétisante (Rf//Lm), le schéma
équivalent devient :
On pose :
➢
1 = 1
: Réactance de fuites au primaire.
➢
2 = 2
: Réactance de fuites au secondaire
a) Schéma équivalent ramené au secondaire
Vu du secondaire, le modèle électrique d ’ un transformateur est :
V1cc
V1
V2
V1
V2
V2

Prof : Z. ERRACHIDI
Lycée Technique AL khawarizmi
Unité : A.D.C
20……/20……
Classe : 2ème BAC - STE
Fonction Alimenter : Transformateurs monophasés
Cours N° : 4
P : 5
On peut faire passer la résistance et la réactance du primaire au secondaire en la multipliant par m2
On obtient :
1: RS = (R2+m2 R1): La résistance du transformateur ramenée au secondaire
2 :XS = (X2 + m2X1): La réactance de fuites magnétiques ramenée au secondaire
➢ Essai en court-circuit pour la détermination de Rs et Xs :
En court-circuit ; on détermine : P1cc= R1 
+ R2   (on néglige les pertes Fer)
P1cc= m2R1 
+ R2   car = m2 
P1cc= (m2R1+ R2) 
Zs= m. 
Alors : Avec ZS = 
 donc Xs= 
Rs = 
4) Essai en charge (chute de tension en charge) :
On choisit l’impédance de charge Zc , telle que le transformateur fonctionne aux conditions
nominales de tension et de courant. On définit la chute de tension ΔV=V20-V2 comme la différence
des tensions secondaires à vide et en charge.
D’après le modèle ramené au secondaire :
Ce qui donne par projection : Δ =
20 – 2 =
s
2 cos 2 +
s
2 sin 2