2.Resume Generalites.sur.les.fonctions

Lycée Rue Ahmed Amara Le Kef
Habib Gammar
Généralités Sur Les
Fonctions
2e Sc
1 / 2
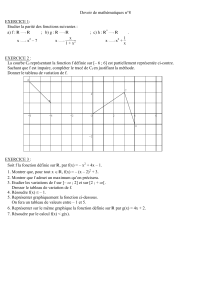
Résumé : Généralités sur les fonctions
2e Sc
❖ Vocabulaire
 Une fonction est une relation qui permet d’associer à un nombre
x
, au plus un autre nombre
()fx
appelé image de
x
. On note
:f E F→
()x f x
• L’ensemble
E
est appelé ensemble de départ, dans lequel appartient
x
.
• L’ensemble
F
est appelé ensemble d’arrivé, dans lequel appartient
()fx
.
• On dit que
()fx
est l’image du réel
x
.
• On dit que
x
est un antécédent de
()fx
.
❖ L’ensemble de définition
 L’ensemble de définition d’une fonction
f
est l’ensemble des nombres réels qui possèdent une image
par cette fonction, noté
f
D
.
 Exemple : L’ensemble de définition de la fonction
f
définie par
3
() 2
x
fx x
=−
est
\ 2 ] ,2[ ]2, [
f
D= = −   +
❖ Représentation graphique d’une fonction
Le plan est muni d’un repère
( , , )O i j
.
 Soit
f
une fonction définie sur un ensemble
E
.
On appelle représentation graphique de
f
, ou courbe de
f
, notée
f
C
,
l’ensemble des points
( )
, ( )M x f x
, où
xE
.
( , ) f M a b C
()
aE
f a b
=
❖ Sens de variation d’une fonction
 Soit
f
une fonction définie sur un ensemble
E
et
I
un intervalle inclus dans
E
.
 La fonction
f
est croissante sur
I
si, pour tous réels
,a b I
tels que
ab
,
( ) ( )f a f b
.
 La fonction
f
est décroissante sur
I
si, pour tous réels
,a b I
tels que
ab
,
( ) ( )f a f b
.
 La fonction
f
est constante sur
I
si, pour tous réels
,a b I
,
( ) ( )f a f b=
.
 Une fonction est dite monotone sur
I
si elle est soit croissante sur
I
soit décroissante sur
I
.
f
est croissante sur
I
f
est décroissante sur
I
f
est constante sur
I

Résumé : Généralités sur les fonctions
2e Sc
2 / 2
2 / 2
Résumé : Généralités sur les fonctions
2e Sc
❖ Maximum et minimum
 Soit
f
une fonction définie sur un intervalle
I
et
aI
.
 La fonction
f
admet un minimum en
a
sur un intervalle
I
, lorsque :
Pour tout réel
x
de
I
,
( ) ( )f x f a
. Le réel
()fa
est le minimum de
f
sur
I
.
 La fonction
f
admet un maximum en
a
sur un intervalle
I
, lorsque :
Pour tout réel
x
de
I
,
( ) ( )f x f a
. Le réel
()fa
est le maximum de
f
sur
I
.
 La fonction
f
admet un minimum en
a
de valeur
()m f a=
 La fonction
f
admet un maximum en
b
de valeur
()M f b=
❖ Fonction paire
Le plan est muni d’un repère orthogonal
( , , )O i j
.
 Soit
f
une fonction définie sur
E
.
f
est paire
: ( ) ( )
xE
xE f x f x
−
   −=
 Si
f
est paire alors
f
C
est symétrique par rapport à l’axe
( , )Oj
.
❖ Fonction impaire
Le plan est muni d’un repère orthogonal
( , , )O i j
.
 Soit
f
une fonction définie sur
E
.
f
est impaire
: ( ) ( )
xE
xE f x f x
−
   − = −
 Si
f
est impaire alors
f
C
est symétrique par rapport à
O
.