TD

Exercice 1
Envisagez d'appliquer l'algorithme du perceptron par l'origine sur la base d'un petit ensemble de formation contenant trois
points :
x
(
1
)
= [-1, -1]
x
(2)
= [1, 0]
x
(3)
= [-1, 1.5]
y
(1)
= 1
y
(2)
= -1
y
(3)
= 1
Étant donné que l'algorithme de Perceptron commence par θ
(0)
= 0, le premier point que l'algorithme voit est toujours considéré
comme une erreur. L'algorithme commence par un point de données et passe ensuite à travers les données (dans l'ordre) jusqu'à
ce qu'il ne fasse plus d'erreur.
1. Combien d'erreurs l'algorithme fait-il jusqu'à la convergence si l'algorithme commence par le point de données x
(1)
?
Combien d'erreurs l'algorithme fait-il s'il commence par le point de données x
(2)
?
Indiquez également la progression du plan de séparation au fur et à mesure des cycles de l'algorithme dans le format
de liste suivant :
(
)
(
)
[
]
(
)
(
)
[
]
[
]
NN 21 1
2
1
1
,,..., θθθθ
où l'exposant indique un θ différent au fur et à mesure que le plan de
séparation progresse. Par exemple, si θ passe de [0,0] (initialisation) à [1,2] puis à [3,-2], vous devez entrer [[1,2], [3,-
2]].
2. Dans la partie (a), quels sont les facteurs qui influent sur le nombre d'erreurs commises par l'algorithme ?
Note : Ne choisissez que les facteurs qui ont été modifiés dans la partie (a), et non tous les facteurs qui peuvent
affecter le nombre d'erreurs.
 Ordre d'itération
 Marge maximale entre les points de données positifs et négatifs
 Norme maximale des points de données
3. Supposons maintenant que x(3)=[-1,10] . Combien d'erreurs l'algorithme fait-il jusqu'à la convergence si le cycle
commence au point de données x(1) ?
Indiquez également la progression du plan de séparation au fur et à mesure que l'algorithme effectue des cycles dans
le format de liste suivant :
(
)
(
)
[
]
(
)
(
)
[
]
[
]
NN 21 1
2
1
1
,,..., θθθθ
où l'exposant indique un θ différent au fur et à mesure que le plan
de séparation progresse. Par exemple, si θ passe de [0,0] (initialisation) à [1,2] puis à [3,-2], vous devez entrer [[1,2],
[3,-2]].
4. Pour un ordre d'itération fixe, quels sont les facteurs qui affectent le nombre d'erreurs commises par l'algorithme entre
la partie (a) et la partie (c) ?
Note : Ne choisissez que les facteurs qui ont été modifiés entre la partie (a) et la partie (c), et non tous les facteurs qui
peuvent affecter le nombre d'erreurs
 Ordre d'itération
 Marge maximale entre les points de données positifs et négatifs
 Norme maximale de points de données corrects

Exercice 2
Dans cette question, nous utiliserons l'algorithme des projections alternées pour la factorisation de la matrice de rang inférieur,
qui vise à minimiser
( )
[ ]
( )
( )
     tion Régularisa equadratiquErreur
222
1
,
, 1 1 1 1
22
2
∑ ∑∑ ∑∑
∈ = = = =
++−=
Dia
n
a
k
j
m
i
k
jijaj
ai
T
ai
VUUVYVUJ
λλ
Dans la suite, nous appellerons le premier terme le terme d'erreur quadratique, et les deux termes avec λ les termes de
régularisation.
=
63?
??4
?2?
7?5
comme défini Soit YY
D est défini comme l'ensemble des indices (a,i), où Y
a,i
n'est pas manquant. Dans ce problème, on laisse k = λ = 1 . De plus, U
et V sont initialisés comme U
(0)
= [6, 0, 3, 6]
T
, et V
(0)
= [4, 2, 1]
T
.
1. Calculer X
(0)
, la matrice des classements prévus des UV
T
compte tenu des valeurs initiales de U
(0)
et V
(0)
.
2. Calculer le terme d'erreur quadratique (EQ) et les termes de régularisation (REG) pour l'estimation actuelle X .
3. Supposons que le V soit maintenu fixe. Exécutez une étape de l'algorithme pour trouver la nouvelle estimation U(1) .
Formulez U(1) sous forme de liste de nombres
(
)
(
)
(
)
(
)
],,,[
1
4
1
3
1
2
1
1
UUUU .

Exercice 3
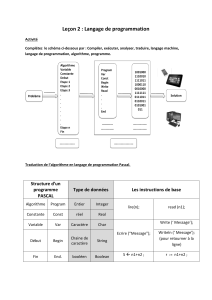
Dans ce problème, nous allons analyser un simple réseau de neurones pour comprendre ses propriétés de classification.
Considérons le réseau de neurones donné dans la figure ci-dessous, avec des fonctions d'activation ReLU (désignées par f ) sur
tous les neurones, et une fonction d'activation softmax dans la couche de sortie :
Etant donné une entrée x = [x
1
, x
2
]
T
, les unités cachées dans le réseau sont activées par étapes, comme le décrivent les
équations suivantes :
012121111
wwxwxz ++=
022221212
wwxwxz ++=
032321313
wwxwxz ++=
042421414
wwxwxz ++=
(
)
(
)
0,max
11
zzf
=
(
)
(
)
0,max
22
zzf
=
(
)
(
)
0,max
33
zzf =
(
)
(
)
0,max
44
zzf
=
(
)
(
)
(
)
(
)
413132121111
4vzfvzfvzfvzfu +++=
(
)
(
)
(
)
(
)
423232221212
4vzfvzfvzfvzfu +++=
(
)
(
)
0,max
11
uuf
=
(
)
(
)
0,max
11
uuf
=
La sortie finale du réseau est obtenue en appliquant la fonction softmax à la dernière couche cachée,
(
)
( ) ( )
21
1
1ufuf
uf
e
e
e
o
+
=
(
)
( ) ( )
21
2
2ufuf
uf
e
e
e
o
+
=
Dans ce problème, nous considérerons les paramètres suivant:
−− −− −
−
=
110
101
110
101
042414
032313
022212
012111
www
www
www
www
−−−−
=
21111
01111
0242322212
0141312111
vvvvv
vvvvv
1. Considérez l'entrée x
1
= 3, x
2
= 14. Quelle est la sortie finale (o1, o2) du réseau? (donner les résultats à au moins 9
décimales après la virgules)
w
11
w
21
w
12
w
22
w
13
w
23
w
14
w
24
z
1
z
2
z
3
z
4
f(z
1
)
f(z
2
)
f(z
3
)
f(z
4
)
v
11
v
12
v
21
v
22
v
31
v
32
v
41
v
42
u
1
u
2
o
1
o
2
x
1
x
2

2. Dans ce problème, nous visualisons les "limites de décision" dans l'espace x, correspondant aux quatre unités cachées.
Ce sont les lignes dans l'espace x où les valeurs de z
1
, z
2
, z
3
, z
4
sont exactement zéro. Tracez les limites de décision des
quatre unités cachées en utilisant les paramètres de w fournis ci-dessus.
3. En utilisant la même matrice V que ci-dessus, quelle est la valeur de o
1
(précise à au moins trois décimales si la
réponse est numérique) dans les trois cas suivants ?
En supposant que f (z
1
) + f (z
2
) + f (z
3
) + f (z
4
) = 1
En supposant que f (z
1
) + f (z
2
) + f (z
3
) + f (z
4
) = 0
En supposant que f (z
1
) + f (z
2
) + f (z
3
) + f (z
4
) = 3
4. Maintenant, supposons que nous modifions la fonction softmax du réseau comme suit:
(
)
( ) ( )
21
1
1ufuf
uf
e
e
e
o
ββ
β
+
=
(
)
( ) ( )
21
2
2ufuf
uf
e
e
e
o
ββ
β
+
=
où β > 0 est un paramètre. Notez que notre précédent paramètre correspondait au cas particulier β = 1. Dans la suite,
veuillez écrire une solution numérique avec une précision d'au moins 3 décimales.
Pour β = 1 si notre objectif es d'avoir o
2
≥ 1/1000 f (u
1
) - f (u
2
) doit être inférieur ou égal à une valeur val, calculer val.
Si nous augmentons la valeur à β = 3 , afin de satisfaire à o
2
≥1/1000 , la valeur de f (u
1
) - f (u
2
) devrait être inférieure
ou égale à quelle valeur de val ?
En général, pour satisfaire o
2
≥1/1000, l'augmentation de la valeur de β peut entraîner une valeur f (u
1
) - f (u
2
) :
 Plus petite
 Plus grande