Dioptre sphérique(1)

DIOPTRE SPHÉRIQUE
DIOPTRE SPHÉRIQUE
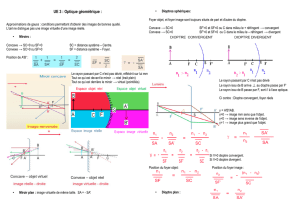
Définition : Un dioptre sphérique est une surface sphérique
réfringente, séparant deux milieux homogènes et transparents
d’indice différents.
+
+
n
C : centre
Concave : SC  0
n’
S : sommet
n
S
n’
C
Convexe : SC >0
1
1. Les relations de conjugaison et de grandissement
Relation de conjugaison
Origine au sommet :
Origine au centre :
Origine aux foyers :
Relation de grandissement
𝑨′𝑩′
𝒏 𝑺𝑨′
𝜸=
=
𝒏′ 𝑺𝑨
𝑨𝑩
𝑨′𝑩′ 𝑪𝑨′
𝜸=
=
𝑨𝑩
𝑪𝑨
𝑨′𝑩′ −𝒇 −𝑭′𝑨′
𝜸=
=
=
𝒇′
𝑨𝑩
𝑭𝑨
2. Foyer objet, distance focale objet et plan
focal objet
❖ Foyer objet : C’est le point conjugué dont l’image est à
l’infini sur l’axe optique.
n
n'
n − n'
−
=
SA SA'
SC
P.F.O
n’
objet A au foyer
n
A
⇒
A′ à l’
F
f : distance focale objet
F : foyer objet
𝑛
𝑆𝐴
=
image A’ à l’infini
𝑛
𝑆𝐹
=
𝑛 − 𝑛′
𝑆𝐶
n
f = SF = SC
n − n'
Le plan perpendiculaire à l’axe optique en F est le plan focal objet.
3
3. Foyer image, distance focale image et
plan focal image
❖ Foyer image : C’est le point conjugué dont l’objet est à l’infini
sur l’axe optique.
n
n'
n − n'
−
=
SA SA'
SC
P.F.I
n
A à l’
objet A à l’infini
n’
A′
F’
F’ : foyer image
f’ : distance focale image
image A’ au foyer image
n'
n'−n

=
SF' SC
n'
f'= SF' = SC
n'−n
Le plan perpendiculaire à l’axe optique en F est le plan focal image.
4
Remarques

F

S
C
F’
n'
n
n'
n
−
=
=−
SF
SA' SA SF'
On a :
;
 Les distances focales ont des signes opposés.
 Les foyers sont tous les deux réels ou tous les deux virtuels.
Le milieu du segment [FF] coïncide avec celui du segment [SC]
Il n’y a jamais de foyer entre S et C.
Ces relations permettent de placer un foyer quand on connaît l’autre.
5
4. Vergence d’un dioptre
C’est la quantité :
n' −n
n'
n
V =
=
=−
SF
SC
SF'
mesurée en dioptrie ()
qd R est en (m)
Si V > 0 (f > 0)
dioptre convergent
Si V < 0 (f < 0)
dioptre divergent
6
Dioptres convergents
Concave
V =
n' −n
n'
n
=
=−
SF
SC
SF'
n > n’
n
Dioptre convergent
Convexe
n
n
n < n’
n
Dioptre convergent
Un dioptre est convergent si les foyers sont réels et son
centre C est situé dans le milieu le plus réfringent .
7
Dioptres divergents
Concave
n
n < n’
n
Dioptre divergent
n' −n
n'
n
V =
=
=−
SF
SC
SF'
Convexe
n
n > n’
n
Dioptre divergent
Un dioptre est divergent si les foyers sont virtuels et son
centre C est situé dans le milieu le moins réfringent .
8
5. Construction de l’image d’un objet AB

Utilisation de 3 rayons particuliers :
n1
n1>n2
n2
B
F’
A
F
C
A’
S
B’
Tout rayon // à l’axe optique émerge du (DS) en passant par F’.
Tout rayon passant par le centre C du dioptre n’est pas dévié.
Tout rayon passant par F ressort du (DS) // à l’axe optique.
9
5. Construction de l’image d’un objet AB
n < n
Dioptre divergent
n
B
n′
B′
A
F’
A′ C
S
F
10
6. Foyers secondaires, Plan focal objet et
Plan focal image
PFO
PFO
Φ
F
S
C
n
F
F′
n′
PFO : plan focal objet
Φ ( foyer secondaire objet).
PFI
PFI
F′
F′
F
n
n′
Φ′ ( foyer secondaire image).
Φ′
PFI : plan focal image
11
6- a Construction d’un rayon quelconque
(En utilisant le foyer secondaire image)
Tous les rayons parallèles à AI convergent à la sortie en Φ′
( foyer secondaire image).
n
I
n′
Φ
A
F
PFI
C
S
F′
Dioptre convergent (n > n′ )
✓ Tout point appartenant au plan focal image est appelé foyer
secondaire image Φ′ .
12
6-b Construction d’un rayon quelconque
(En utilisant le foyer secondaire objet)
➢On cherche l'intersection du rayon incident avec le plan
focal objet.
➢On trace un rayon passant par le centre C du dioptre et le
foyer secondaire .
PFO
n
n′
I
Φ
A’
A
F
C
S
F’
Dioptre convergent (n > n′ )
Le rayon réfracté est parallèle à C 
13
Chap. 2 Miroirs et dioptres
Cas du dioptre plan
Equivalent au : Dioptre sphérique de rayon infini
Dioptre Sphérique
n
n'
=
SA SA'
Relation de
conjugaison
Grandissement
Dioptre plan
A' B' n SA'
g=
=
n' SA
AB
g=1
14
Equivalent au Miroir sphérique n’=-n
Les relations de conjugaison et de grandissement d’un MS se
déduisent de celles d’un dioptre sphérique en posant : n′ = - n
Dioptre sphérique
Miroir sphérique
relations de conjugaison avec :
origine au
sommet
1
1
2
+
=
CA CA' CS
origine
au centre
origine aux
foyers
Grandissement linéaire
g=
A' B' n SA'
=
n' SA
AB
Formule de Lagrange Helmholtz
g G = −1
15