Numéro de candidat : ………………………..
COLLÈGE LE CLERGEON 28 avril 2010
ÉPREUVE DU BREVET BLANC DE MATHÉMATIQUES
- La calculatrice ainsi que les instruments de géométrie sont autorisés.
- Toute réponse doit être justifiée.
- La qualité, la clarté, la précision des raisonnements ainsi que l’orthographe et la présentation
seront prises en compte dans l’appréciation des copies : 4 points.
- Le sujet est à rendre avec la copie
- Durée de l'épreuve : 2 heures
Partie I – Activités numériques (12 points)
Dans toute cette partie, on fera apparaître les étapes de chaque calcul sur la copie.
EXERCICE 1 (4 points)
On donne A = 1 – ( ; B = ; C =
a) Écrire A, B et C sous la forme d'une fraction.
b) Montrer que la somme A + B + C est un nombre entier.
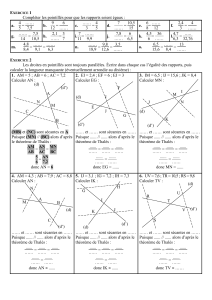
EXERCICE 2 (4,5 points)
On considère l'expression M dont une écriture est la suivante : M = (3x + 5) ² – (2x + 7)² .
a) Développer et réduire l'expression M.
b) Factoriser l'expression M.
c) Calculer M pour x = – 3.
d) Résoudre l'équation (x – 2)(5x + 12)= 0.
EXERCICE 3 (3,5 points)
GDHE est un rectangle et DCBH est un trapèze.
On cherche pour quelles valeurs de x l’aire de GDHE est supérieure à
celle de DCBH.
On rappelle la formule de l’aire d’un trapèze :
A
trapèze =
a) Donner les valeurs entre lesquelles le nombre x peut varier.
b) Parmi les trois inéquations proposées ci-dessous, laquelle correspond au problème ? Justifier.
4x > 30 – 4x ; 4x > 30 ; 2x + 8 > 19
c) Résoudre cette inéquation puis conclure.

32°
4,3m
H
S
A
Partie II – Activités géométriques (12 points)
EXERCICE 1 (5 points)
La figure n'est pas faite en vraie grandeur.
Elle n'est pas à reproduire.
Les droites (CD) et (AO) sont perpendiculaires.
On donne : AO = 9 cm, OC= 6 cm ; AB = 15 cm et OB = 12 cm.
a) Démontrer que le triangle ABO est rectangle.
En déduire que les droites (DC) et (OB) sont parallèles.
b) Démontrer en justifiant le raisonnement que CD = 4 cm
c) Calculer la mesure en degrés de l’angle OBD .
On donnera l’arrondi au dixième de degré près.
EXERCICE 2 (3 points)
Sous l’effet de la tempête, un lampadaire s’est cassé en S.
Il est alors composé de deux segments schématisés par [HS]
et [SA] selon le dessin ci-contre.
Le sol, représenté par [HA] est supposé horizontal.
On suppose que, malgré la rupture, [HS] est resté vertical.
On obtient les mesures suivantes :
HAS = 32° et HA = 4,3 m
Calculer, en arrondissant au dm près, la hauteur du lampadaire avant la tempête.
EXERCICE 3 (4 points)
ABCDEFGH est un pavé droit tel que AE = 5 cm ;
EF = 7 cm ; AD = 6 cm.
I est le point de l’arête [FG] tel que IG = 4 cm.
J est le point de l’arête [CG] tel que GJ = 3 cm.
a) Sur la figure en perspective cavalière ci-contre, tracer
la section de ce pavé droit par le plan parallèle
à l’arête [AB] et passant par les points I et J.
b) Quelle est la nature de cette section ? Justifier.
c) Calculer IJ et en déduire l’aire de cette section.

Partie III – Problème (12 points)
Sarah et Julien possèdent un téléphone portable et veulent choisir l'abonnement mensuel le plus adapté à
leur besoin. Ils ont sélectionné les trois tarifs suivants :
Tarif 1 : Le montant de la facture de téléphone en fonction du temps de communication est représenté
par le graphique donné en annexe sur la dernière page.
Tarif 2 : 0,55 € la minute de communication
Tarif 3 : un abonnement mensuel de 10 € auquel s’ajoute 0,35 € par minute de communication.
Tous les montants des factures de téléphone seront exprimés en euros et les temps de communication en
minutes.
Partie A - Étude du tarif 1
On considère dans cette partie le montant de la facture de téléphone quand le tarif 1 a été choisi.
1. Donner, par lecture graphique, le montant de la facture pour 20 minutes de communication.
(Marquer sur le graphique de l'annexe les pointillés nécessaires à cette lecture).
2. Donner, par lecture graphique, la durée en minutes des communications qui correspond à une facture
de 35 € (marquer sur le graphique de l'annexe les pointillés nécessaires à cette lecture).
3. Le montant de la facture selon le tarif 1 est-il proportionnel à la durée des communications ?
Justifier votre réponse.
Partie B - Étude du tarif 2
On considère dans cette partie le montant de la facture de téléphone quand le tarif 2 a été choisi.
1. Compléter le tableau intitulé «Étude du tarif 2» situé dans l'annexe.
2. Si x représente la durée des communications (en minutes) pour un mois avec le tarif 2, donner une
expression du montant de la facture en fonction de x.
3. Soit la fonction f définie par f(x) = 0,55x; représenter graphiquement la fonction f dans le repère de
l'annexe (le même repère que le graphique correspondant au tarif 1).
Partie C - Étude du tarif 3
On considère dans cette partie le montant de la facture de téléphone quand le tarif 3 a été choisi.
1. Compléter le tableau intitulé «Étude du tarif 3» situé dans l'annexe.
2. Si x représente la durée des communications (en minutes) pour un mois avec le tarif 3, donner une
expression du montant de la facture en fonction de x.
3. Soit la fonction g définie par g(x) = 0,35x + 10; représenter graphiquement la fonction g dans le repère
de l'annexe (le même repère que le graphique correspondant au tarif 1).
4. Le montant de la facture selon le tarif 3 est-il proportionnel à la durée des communications ?
Justifier votre réponse.
Partie D - Comparaison des tarifs
1. Sarah a besoin de téléphoner 1 h 30 min par mois. Donner par lecture graphique le tarif le plus
avantageux pour elle et marquer sur le graphique les pointillés nécessaires à cette lecture.
2. Julien ne veut pas dépenser plus de 20 € par mois pour ses communications tout en souhaitant pouvoir
téléphoner le plus possible. Donner par lecture graphique le tarif le plus avantageux pour lui et marquer
sur le graphique les pointillés nécessaires à cette lecture.
3. Résoudre l'inéquation 0,55x 0,35x + 10 .
Interpréter cette inéquation et sa résolution en termes de comparaison de tarifs.

ANNEXE
Étude du tarif 2
Nombres de minutes de communication
20
100
Montant de la facture en euro selon le tarif 2
22
Étude du tarif 3
Nombres de minutes de communication
20
100
Montant de la facture en euro selon le tarif 3

BARÈME
Partie I – Activités numériques (12 points)
Exercice 1 (4 points)
a) 3 points : A = 1 point ; B = 1,5 point ; C = 1 point
b) 0,5 point
Exercice 2 (4,5 points)
a) 1,5 point
b) 1,5 point
c) 0,5 point
d) 1 point
Exercice 3 (3,5 points)
a) 0,5 point.
b) 1,5 point : 4x > 30 – 4x : 0,5 point et justification : 1 point
c) 1,5 point : Résolution : 1 point et conclusion : 0,5 point.
Partie II – Activités géométriques (12 points)
Exercice 1 (5 points)
a) 2 points : ABO rectangle en O sur 1,5point et (DC) et (OB) parallèles sur 0,5 point.
b) 1,5 point
c) 1,5 point (dont 0,5 pour l’arrondi au dixième)
Exercice 2 (3 points)
1 point pour HS
1 point pour SA
1 point pour la hauteur complète (dont 0,5 pour l’arrondi au dm)
Exercice 3 (4 points)
a) 1 point (ne pas sanctionner si arêtes cachées pas faites en pointillés)
b) 1 point
c) 1 point
Partie III – Problème (12 points)
Pointillés pour réponses graphiques : 0,5 point en tout.
Partie A - Étude du tarif 1 (2 points)
1. 0,5 point
2. 0,5 point
3. 1 point
Partie B - Étude du tarif 2 (2,5 points)
1. 1 point
2. 0,5 point
3. 1 point
Partie C - Étude du tarif 3 (4 points)
1 point par question
Partie D - Comparaison des tarifs (3 points)
1. 0,5 point
2. 1 point
3. 1,5 point
1
/
5
100%