
Internal Report SUF–PFY/96–01
Stockholm, 11 December 1996
1st revision, 31 October 1998
last modification 10 September 2007
Hand-book on
STATISTICAL
DISTRIBUTIONS
for
experimentalists
by
Christian Walck
Particle Physics Group
Fysikum
University of Stockholm
(e-mail: [email protected])


Contents
1 Introduction 1
1.1 Random Number Generation .............................. 1
2 Probability Density Functions 3
2.1 Introduction ........................................ 3
2.2 Moments ......................................... 3
2.2.1 Errors of Moments ................................ 4
2.3 Characteristic Function ................................. 4
2.4 Probability Generating Function ............................ 5
2.5 Cumulants ......................................... 6
2.6 Random Number Generation .............................. 7
2.6.1 Cumulative Technique .............................. 7
2.6.2 Accept-Reject technique ............................. 7
2.6.3 Composition Techniques ............................. 8
2.7 Multivariate Distributions ................................ 9
2.7.1 Multivariate Moments .............................. 9
2.7.2 Errors of Bivariate Moments .......................... 9
2.7.3 Joint Characteristic Function .......................... 10
2.7.4 Random Number Generation .......................... 11
3 Bernoulli Distribution 12
3.1 Introduction ........................................ 12
3.2 Relation to Other Distributions ............................. 12
4 Beta distribution 13
4.1 Introduction ........................................ 13
4.2 Derivation of the Beta Distribution ........................... 13
4.3 Characteristic Function ................................. 14
4.4 Moments ......................................... 14
4.5 Probability Content ................................... 14
4.6 Random Number Generation .............................. 15
5 Binomial Distribution 16
5.1 Introduction ........................................ 16
5.2 Moments ......................................... 16
5.3 Probability Generating Function ............................ 16
5.4 Cumulative Function ................................... 17
5.5 Random Number Generation .............................. 17
5.6 Estimation of Parameters ................................ 17
5.7 Probability Content ................................... 18
6 Binormal Distribution 20
6.1 Introduction ........................................ 20
6.2 Conditional Probability Density ............................. 21
6.3 Characteristic Function ................................. 21
6.4 Moments ......................................... 21
6.5 Box-Muller Transformation ............................... 22
6.6 Probability Content ................................... 23
i

6.7 Random Number Generation .............................. 24
7 Cauchy Distribution 26
7.1 Introduction ........................................ 26
7.2 Moments ......................................... 26
7.3 Normalization ....................................... 27
7.4 Characteristic Function ................................. 27
7.5 Location and Scale Parameters ............................. 27
7.6 Breit-Wigner Distribution ................................ 28
7.7 Comparison to Other Distributions ........................... 28
7.8 Truncation ........................................ 29
7.9 Sum and Average of Cauchy Variables ......................... 30
7.10 Estimation of the Median ................................ 31
7.11 Estimation of the HWHM ................................ 31
7.12 Random Number Generation .............................. 33
7.13 Physical Picture ..................................... 34
7.14 Ratio Between Two Standard Normal Variables .................... 35
8 Chi-square Distribution 36
8.1 Introduction ........................................ 36
8.2 Moments ......................................... 36
8.3 Characteristic Function ................................. 37
8.4 Cumulative Function ................................... 38
8.5 Origin of the Chi-square Distribution .......................... 38
8.6 Approximations ...................................... 39
8.7 Random Number Generation .............................. 39
8.8 Confidence Intervals for the Variance .......................... 40
8.9 Hypothesis Testing .................................... 40
8.10 Probability Content ................................... 40
8.11 Even Number of Degrees of Freedom .......................... 42
8.12 Odd Number of Degrees of Freedom .......................... 42
8.13 Final Algorithm ...................................... 43
8.14 Chi Distribution ..................................... 43
9 Compound Poisson Distribution 45
9.1 Introduction ........................................ 45
9.2 Branching Process .................................... 45
9.3 Moments ......................................... 45
9.4 Probability Generating Function ............................ 45
9.5 Random Number Generation .............................. 46
10 Double-Exponential Distribution 47
10.1 Introduction ........................................ 47
10.2 Moments ......................................... 47
10.3 Characteristic Function ................................. 47
10.4 Cumulative Function ................................... 48
10.5 Random Number Generation .............................. 48
ii

11 Doubly Non-Central F-Distribution 49
11.1 Introduction ........................................ 49
11.2 Moments ......................................... 49
11.3 Cumulative Distribution ................................. 50
11.4 Random Number Generation .............................. 50
12 Doubly Non-Central t-Distribution 51
12.1 Introduction ........................................ 51
12.2 Moments ......................................... 51
12.3 Cumulative Distribution ................................. 52
12.4 Random Number Generation .............................. 52
13 Error Function 53
13.1 Introduction ........................................ 53
13.2 Probability Density Function .............................. 53
14 Exponential Distribution 54
14.1 Introduction ........................................ 54
14.2 Cumulative Function ................................... 54
14.3 Moments ......................................... 54
14.4 Characteristic Function ................................. 54
14.5 Random Number Generation .............................. 55
14.5.1 Method by von Neumann ............................ 55
14.5.2 Method by Marsaglia .............................. 55
14.5.3 Method by Ahrens ................................ 56
15 Extreme Value Distribution 57
15.1 Introduction ........................................ 57
15.2 Cumulative Distribution ................................. 58
15.3 Characteristic Function ................................. 58
15.4 Moments ......................................... 58
15.5 Random Number Generation .............................. 60
16 F-distribution 61
16.1 Introduction ........................................ 61
16.2 Relations to Other Distributions ............................ 62
16.3 1/F ............................................ 62
16.4 Characteristic Function ................................. 62
16.5 Moments ......................................... 62
16.6 F-ratio ........................................... 63
16.7 Variance Ratio ...................................... 64
16.8 Analysis of Variance ................................... 65
16.9 Calculation of Probability Content ........................... 65
16.9.1 The Incomplete Beta function .......................... 66
16.9.2 Final Formulæ .................................. 67
16.10 Random Number Generation .............................. 68
iii
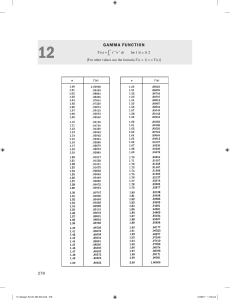
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
 17
17
 18
18
 19
19
 20
20
 21
21
 22
22
 23
23
 24
24
 25
25
 26
26
 27
27
 28
28
 29
29
 30
30
 31
31
 32
32
 33
33
 34
34
 35
35
 36
36
 37
37
 38
38
 39
39
 40
40
 41
41
 42
42
 43
43
 44
44
 45
45
 46
46
 47
47
 48
48
 49
49
 50
50
 51
51
 52
52
 53
53
 54
54
 55
55
 56
56
 57
57
 58
58
 59
59
 60
60
 61
61
 62
62
 63
63
 64
64
 65
65
 66
66
 67
67
 68
68
 69
69
 70
70
 71
71
 72
72
 73
73
 74
74
 75
75
 76
76
 77
77
 78
78
 79
79
 80
80
 81
81
 82
82
 83
83
 84
84
 85
85
 86
86
 87
87
 88
88
 89
89
 90
90
 91
91
 92
92
 93
93
 94
94
 95
95
 96
96
 97
97
 98
98
 99
99
 100
100
 101
101
 102
102
 103
103
 104
104
 105
105
 106
106
 107
107
 108
108
 109
109
 110
110
 111
111
 112
112
 113
113
 114
114
 115
115
 116
116
 117
117
 118
118
 119
119
 120
120
 121
121
 122
122
 123
123
 124
124
 125
125
 126
126
 127
127
 128
128
 129
129
 130
130
 131
131
 132
132
 133
133
 134
134
 135
135
 136
136
 137
137
 138
138
 139
139
 140
140
 141
141
 142
142
 143
143
 144
144
 145
145
 146
146
 147
147
 148
148
 149
149
 150
150
 151
151
 152
152
 153
153
 154
154
 155
155
 156
156
 157
157
 158
158
 159
159
 160
160
 161
161
 162
162
 163
163
 164
164
 165
165
 166
166
 167
167
 168
168
 169
169
 170
170
 171
171
 172
172
 173
173
 174
174
 175
175
 176
176
 177
177
 178
178
 179
179
 180
180
 181
181
 182
182
 183
183
 184
184
 185
185
 186
186
 187
187
 188
188
 189
189
 190
190
 191
191
 192
192
 193
193
 194
194
 195
195
 196
196
 197
197
 198
198
 199
199
 200
200
 201
201
 202
202
1
/
202
100%


![[faculty.baruch.cuny.edu]](http://s1.studylibfr.com/store/data/008196527_1-00094098ced89faa02164e141a3c1389-300x300.png)
![[www.stat.berkeley.edu]](http://s1.studylibfr.com/store/data/009890385_1-17b8a124e5f43be1710b615279a22a09-300x300.png)


