ccc

1/5
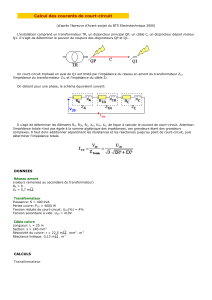
Calcul des courants de court-circuit
Transformateur
SN = 1000 kVA
U20 = 410v
UCC% = 5%
PJ = 10 kW
Transformateur
SN = 1000 kVA
U20 = 410v
UCC% = 5%
PJ = 10 kW
Jeu de barres
3 barres cuivre de 400 mm² / phase
longueur 10 m
3 câbles unipolaires de 400 mm²
aluminium
longueur 80 m
Moteur 50 kW
 = 0,9
cos = 0,8
uCC = 25%
Câble cuivre
35mm²
longueur 30m
A
B
C
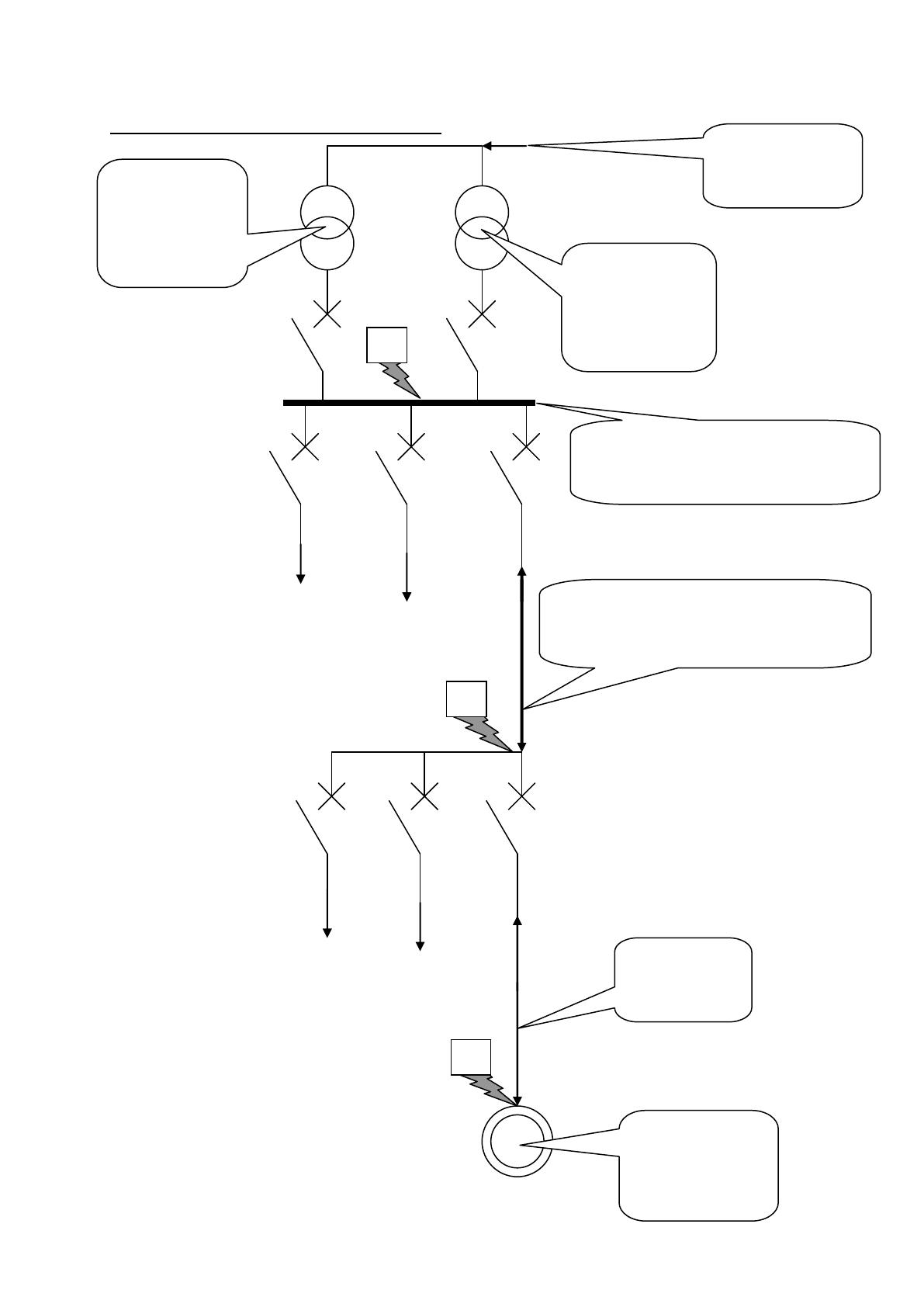
Réseau amont
20 kV
PCC = 500 MVA
C1
C2

2/5
Transformateurs:
Les deux transformateurs sont identiques.
Données relatives à un transformateur:
SN = 1000 kVA U20 = 410v UCC% = 5% PJ = 10 kW
Les calculs suivants sont destinés à déterminer la résistance et la réactance par phase d'un
transformateur. Les transformateurs étant identiques et fonctionnant en parallèle, ces valeurs
sont à diviser par 2 pour déterminer le courant de court-circuit.
Le courant nominal du transformateur est :
A 1408
4103
1000.10
U3
S
I -3
20
N
N
Les pertes Joule sont dissipées dans les 3 résistances RTR, d'où la valeur de la résistance par
phase du transformateur:
m 1,68
1408310.10 I3 P
R 2
3
2
N
J
TR
Ucc est la valeur de la tension U20 qui donnerait le courant nominal quand le secondaire du
transformateur est en court-circuit. Le schéma équivalent par phase est:
L'impédance par phase du transformateur est:
m 8,40
1000.10 100 410 5
S
U
100
5
U3
S
3100
U5
I3
U
Z 3
2
N
2
20
20
N
20
N
CC
TR
La réactance par phase du transformateur s'obtient par:
 m 8,23 1,68 - 8,40 R - Z X 222
TR
2
TRTR
Pour les deux transformateurs en parallèle:
RTR = 0,84 m
XTR = 4,11 m
ZTR
UCC
IN

3/5
Disjoncteurs:
En BT, la résistance peut être négligée, la réactance est XDJ = 0,15 m
Jeu de barres:
La réactance est de 0,15 m / m
La résistance se détermine par:
S
L
RB
Avec:  = 22,5 m.mm²/m pour le cuivre et 36 m.mm²/m pour l'aluminium
L : longueur du jeu de barres
S : section des barres
Câbles:
La résistance se détermine par:
S
L
RC
Avec:  = 22,5 m.mm²/m
L : longueur du câble
S : section du câble
Seule la résistance est prise en compte pour des sections inférieures à 150mm²
Pour des sections supérieures, la réactance moyenne est de 0,08 m / m
Moteur asynchrone:
En cas de court-circuit, le moteur est un générateur
m
3
2
m
2
20
mX m 605
0,8 0,9
50.10
100
410 25
S
U
100
25
Z 
Rm = 0,2 Xm = 0,2  605 = 121 m

4/5
R (m)
X (m)
R (m)
X (m)
Z (m)
22 XR 
ICC (kA)
Z3
410
Réseau amont
0,15
0,78
Transformateurs
1,68 / 2
= 0,84
8,23 / 2
= 4,115
Disjoncteurs
0
0,15 / 2
= 0,075
Jeu de barres
400310
22,5 
= 0,19
0,1510
= 1,5
1,18
6,47
6,57
36
en A
Disjoncteur
0
0,15
Câble C1
400380
36 
= 7,2
0,0880
=6,4
8,38
13,02
15,48
15,3
en B
Disjoncteur
0
0,15
Câble C2
35
30
22,5
= 19,28
0
24,96
13,17
28,22
8,4
en C
A ces courants de court-circuit se rajoutent ceux du moteur considéré comme générateur

5/5
R (m)
X (m)
R (m)
X (m)
Z (m)
22 XR 
ICC (kA)
Z3
410
Moteur
121
605
Câble C2
19,28
0
Disjoncteur
0
0,075
140
605
621
0,38
en B
Câble C1
7,2
6,4
Disjoncteur
0
0,15
Jeu de barres
0,19
1,5
145
613
630
0,37
en A
On constate que ces courants de court-circuit sont négligeables devant ceux déterminés
précédemment
Choix des disjoncteurs:
Disjoncteurs en aval des transformateurs
Pouvoir de coupure > 36 + 0,37 = 36,37 kA  50 kA
Disjoncteur de protection de C1
Pouvoir de coupure > 16,6 + 0,38 = 16,98 kA  20 kA
Disjoncteur de protection de C2
Pouvoir de coupure > 8,4 kA  10 kA