Cours-Transfert-de-chaleur

Chapitre 1 : Modes de transfert de chaleur
Enseignant : A. Benbrik 1
CHAPITRE 1
MODES DE TRANSFERT DE CHALEUR
1. Introduction
L’énergie thermique se transmet d’un point à un autre, dans un même corps, à chaque fois
qu’il existe un gradient de température. Ce phénomène est aussi valable lorsque 2 systèmes, à
températures différentes se mettent en contact. La théorie qui étudie le processus de propagation
de la chaleur porte le nom de transfert ou transmission de chaleur. La chaleur transmise ne peut
être mesurée ou observée directement. Mais les effets qu’elle produit sont observables et
mesurables.
La science qui étudie les relations entre la chaleur et les autres formes d’énergie
s’appelle : thermodynamique. Elle gouverne toutes les transformations d’énergie
quantitativement. Mais ne place pas de restrictions quant à la direction de la transformation.
Tous les processus de transfert de chaleur impliquent la transmission et la conversion
d’énergie. Ils doivent, alors obéir aux premier et deuxième principes de la thermodynamique.
Premier principe : L’énergie ne peut être ni créée ni détruite.
Deuxième principe : La chaleur ne peut être transmise d’une zone à température moins
élevée vers une zone à température plus élevée.
Mais cela ne peut, pour autant, dire que la théorie de transfert de chaleur est dérivée de la
thermodynamique. Car la thermodynamique classique a pour but principal d’étudier les états
d’équilibre mécanique, chimique et même thermique. Alors que le transfert de chaleur est le
résultat de non équilibre de température. Son traitement quantitatif doit se baser sur une autre
branche de la science. Le même raisonnement s’applique aux autres types de processus de
transport tel que celui de masse ou de diffusion.
La thermodynamique classique traite des états de système d’un point de vue
macroscopique et ne fait pas d’hypothèses au sujet de la structure de la matière. L’analyse
thermodynamique permet de décrire l’état d’un système en terme de caractéristiques grossières,
tels que la pression, volume et température qui peuvent être mesurer directement et n’implique
aucune supposition concernant la structure de la matière. Ces variables ou propriétés
thermodynamiques ne sont pas significatives pour le système seulement si elles sont uniformes
durant les transformations. Ainsi, la thermodynamique classique n’est pas concerné par le détail
du processus, mais plutôt, par les états d’équilibre et leurs relations. D’un point de vue
thermodynamique, la quantité de chaleur transmise au cours d’un processus est simplement égale
à la différence des énergies échangées du système et le travail effectué. Il est évident que ce type
d’analyse ne considère ni le mécanisme de l’écoulement de la chaleur ni le temps nécessaire au
transfert de la chaleur. Elle décrit simplement quelle quantité de chaleur faut-il fournir au
système ou la céder durant le processus entre des états spécifiques finaux, sans considérer quand
ni comment ceci peut être accompli. Le fait que cette information ne peut pas être obtenue de
l’analyse thermodynamique résulte de l’absence du temps en tant que variable. La question de
combien de temps va durer le transfert d’une certaine quantité spécifique de chaleur qui malgré
son importance, ne rentre habituellement pas dans l’analyse thermodynamique.
Dans le domaine d’engineering la clef des problèmes consiste à la détermination du taux
de transfert de chaleur correspondant à une différence de température bien spécifique. Pour
estimer le coût, la faisabilité et les dimensions de l’équipement nécessaires à la transmission
d’une certaine quantité de chaleur pour un temps donné, une analyse détaillée du mécanisme de

Chapitre 1 : Modes de transfert de chaleur
Enseignant : A. Benbrik 2
transfert de chaleur doit être réalisée. Les dimensions d’un évaporateur, d’un réchauffeur, d’un
réfrigérateur ou d’un échangeur de chaleur ne dépendent pas seulement de la quantité de chaleur
à transmettre, mais encore du taux auquel cette chaleur sera transférée dans les conditions
données. Le fonctionnement réussi des systèmes de machines tels que les aubes d’une turbine ou
bien les parois d’une chambre de combustion dépend des possibilités de refroidissement de
certaines parties des matériaux par évacuation continue de la chaleur à des taux rapides.
L’analyse de transfert de chaleur doit être aussi réalisée pour le design des machines électriques,
transformateurs et les paliers de roulement afin d’éviter les conditions qui peuvent conduire à
une surchauffe et la détérioration des équipements. Ces exemples montrent que la plupart des
branches d’engineering rencontrent les problèmes de transfert de chaleur dont les solutions ne
proviennent pas du raisonnement thermodynamique seul mais exige une analyse basée sur la
théorie de transfert de chaleur.
En transfert de chaleur, comme dans d’autres branches d’engineering, les solutions
réussies des problèmes nécessitent des suppositions et idéalisations. Il est presque impossible de
décrire exactement un phénomène physique. Ainsi, pour exprimer un problème sous forme
d’équations qui peuvent être résolues il est nécessaire d’introduire des approximations. Dans les
calculs des circuits électriques, par exemple, il est usuel d’assumer que les valeurs de résistances,
capacités et inductances sont indépendantes du courant qui les traverse. Cette supposition
simplifie l’analyse, mais dans certains cas elle peut sérieusement affecté la précision des
résultats. Des approximations similaires sont prises en compte dans les problèmes de transfert de
chaleur. En réalité les propriétés physiques telles que : chaleur spécifique ou la viscosité
changent avec la température. Mais si une valeur moyenne adéquate est choisie, le calcul peut
être considérablement simplifier sans faire d’erreur appréciable dans les résultats finaux.
Le transfert de chaleur peut être défini comme étant le phénomène de transmission de la
chaleur d’une zone à une autre à la base de la différence de température qui existe entre elles.
Etant donné que la différence de température existe dans tout l’univers, le phénomène de
l’écoulement de la chaleur est universel comme ceux associés à l’attraction terrestre. Ce
phénomène étant différent de la gravité terrestre, il n’est pas gouverné par une unique relation,
mais plutôt par une combinaison varié de lois physiques indépendantes.
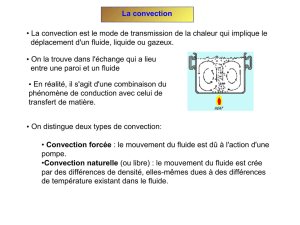
Généralement dans la littérature sur le transfert de chaleur il est reconnu trois modes de
transmission de la chaleur : Conduction, Rayonnement et Convection. Mais, proprement dit, seul
la conduction et le rayonnement doivent être classés en tant que processus de transfert de
chaleur. Parce que c’est les deux seuls mécanismes, qui pour leur opération dépendent
uniquement de l’existence d’une différence de température. L’autre mode qui est la convection
n’est pas tout à fait compatible avec la définition du transfert de chaleur, parce que son opération
dépend aussi du transport mécanique de masse. Mais parce que la convection assure aussi la
transmission d’énergie d’une zone à température élevée vers une autre à faible température, que
l’expression « de transfert de chaleur par convection » est acceptée.
Dans les paragraphes suivants nous passerons en revue les équations de base gouvernant
chaque mode de transfert de chaleur. Le but principal est de faire connaissance de manière
superficielle sans donner trop de détails. Nous commençons par considérer des cas simples. Puis
mettre l’accent sur le cas naturel des transferts de chaleur combinés ou simultanés.

Chapitre 1 : Modes de transfert de chaleur
Enseignant : A. Benbrik 3
1.1 Conduction
Dans un même corps (solide, liquide ou gazeux) si on soumet l’une de ses parties à une
température plus élevée, par exemple, l’équilibre thermique (même température partout) dans
lequel se trouvait ce corps sera rompu et la différence de température (gradient de température)
qui s’installe va engendrer une propagation de la chaleur vers les parties les moins chaudes. Ce
phénomène porte le nom de transfert de chaleur par conduction. L’agitation moléculaire élevée
de la zone chaude communiquera de l’énergie cinétique aux zones plus froides par interactions
de ces dernières. Ce phénomène a lieu sans déplacement de la matière. C’est pour cette raison
que, généralement, la conduction concerne les corps solides. Il en est de même pour les liquides
et gaz, mais dès que le milieu se mets en mouvement ça devient un autre mode de transfert de
chaleur qui est la convection. La conduction est un phénomène de diffusion qui permet donc à la
chaleur de se propager à l’intérieur d’un corps solide. La propagation de la chaleur par
conduction à l’intérieur d’un corps s’effectue selon deux mécanismes distincts : une transmission
par les vibrations des atomes ou molécules et une transmission par la diffusion des électrons
libres.
1.1.1Quelques définitions
Pour bien comprendre les définitions qui suivent prenons un exemple concret de
transfert de chaleur. Considérons le cas d’une barre.
1.1.1.1 Champ de température
Le processus de transfert de chaleur par conduction, comme d’autre modes
d’échange de chaleur, peut avoir lieu uniquement dans le cas où il y a une
différence de température entre les points de ce corps (fig.1). Ce phénomène
s’accompagne d’une variation de température dans l’espace et dans le temps.
L’étude analytique de la conduction conduit à la résolution de l’équation :
t = f(x, y, z, ) (1.1)
Cette équation représente l’expression mathématique du champ de température.
Ainsi, nous définissons le champ de température comme étant l’ensemble des
valeurs de température de tous les points de l’espace étudié dans le temps.
1.1.1.2 Régime temporel
Du point de vue temporel on peut citer les 2 cas possibles de type de
conduction.
La conduction en régime stationnaire appelé aussi régime permanent,
lorsque le température ne dépend pas du temps. Dans ce cas là l’équation
(1.1) s’écrit :
t = f(x, y, z), t
0
Exemple : Si on maintient les extrémités de la barre (fig.1) à des
températures différentes et constantes tout en isolant les surfaces latérales,
z
y
x
t1t2
Fig. 1.1 : Conduction dans une barre
t1>t2

Chapitre 1 : Modes de transfert de chaleur
Enseignant : A. Benbrik 4
on peut constater la stabilité des températures de tous les points de la barre.
Ces températures deviennent constantes et ne varient pas dans le temps.
On peut réaliser cela facilement expérimentalement en plaçant l’extrémité
gauche de la barre dans un récipient d’eau en ébullition (100°C) et
l’extrémité droite dans un autre récipient contenant de la glace fondante
(0°C).
Dans le cas contraire, lorsque la température dépend du facteur temps, on
dit que le régime est instationnaire ou variable (défini par l’équation
(1.1))
Exemple : Dans le cas de la barre (fig.1), entre l’instant initial où la
température de tous les points est la même (équilibre thermique) et l’état
de stabilité des températures de tout ces points et les extrémités à T1et T2,
il y a eu évolution des températures dans le temps.
Pour la résolution des problèmes thermiques on est souvent appeler à rechercher
l’équation de la distribution de la température qui est elle-même celle du champ
de température.
Selon les exigences une étude thermique peut être considérée dans l’un des cas
suivants :
- Unidimensionnelle :
- Stationnaire : t = f(x), t t t
0; 0
y z     ;
- ou instationnaire : t = f(x, ), t t
0
y z   ;
- Bidimensionnelle :
-Stationnaire : t = f(x, y), t t
0; 0
z
- Instationnaire : t = f(x, y, ), t
0
z ;
- Tridimensionnelle :
-Stationnaire : t = f(x, y, z), t
0
- Instationnaire : t = f(x, y, z, )
1.1.1.3 Gradient de température
Dans le cas de la barre (fig. 1), certains points peuvent avoir la même
température. La liaison de ces points donne une surface isotherme. Si on suppose
que les surfaces latérales sont soumises à un échange de chaleur avec le milieu
ambiant et que les points du centre ont des températures plus élevées, on peut
représenter schématiquement les surfaces isothermes dans la barre. Comme un
point ne peut avoir 2 températures différentes, les surfaces isothermes ne se
coupent pas.
La coupe des surfaces isothermes par un plan perpendiculaire à l’une des surfaces
latérales donne un ensemble d’isothermes (fig. 2).
y t1t2
Fig. 1.2 : Surfaces isothermes
t
1
>t
2
Isotherme
x

Chapitre 1 : Modes de transfert de chaleur
Enseignant : A. Benbrik 5
Le plus grand accroissement de température entre des isothermes voisines a lieu
dans la direction normale aux isothermes (fig.3).
Cet accroissement est caractérisé par le gradient de température qui est défini par
la relation mathématique suivante :
n 0
t
l i m g r a d t
n
; 0
t
g r a d t = n
n
où
0
n
est le vecteur unitaire normal à l’isotherme.
∆n : distance entre 2 isothermes voisines.
Le gradient de température est un vecteur dirigé suivant la normale à l’isotherme
dans le sens de l’augmentation de la température. Ainsi, il est opposé au sens de
propagation de la chaleur.
La valeur scalaire du gradient de température
t / n
n’est pas la même pour les
différents points d’une isotherme. Cette valeur est plus grande là où ∆n est plus
petite.
La valeur de
t / n
dans le sens de la propagation de chaleur est négative.
1.1.2 Loi de Fourier (1822)
Le transfert de chaleur spontané dans un corps solide, d’une zone de
température élevée vers une autre zone de température plus basse obéit à la loi
dite de Fourier (établie mathématiquement par Jean Baptiste Biot en 1804 puis
expérimentalement par Fourier en 1822)
Expérience
Considérons l’expérience de la figure 3. Une paroi plane d’un matériau connu est
soumise à 2 sources de chaleur. Le côté gauche est en contact avec l’eau en
ébullition pour maintenir sa température constante à t1=100°C. Le côté droit en
contact de l’eau contenant de la glace permet de maintenir sa température
constante à t2=0°C. Les surfaces en contact avec les liquides sont égales à S. Pour
ne considérer que la propagation de chaleur unidimensionnelle suivant l’axe X,
nous prévoyons une isolation thermique des surfaces latérales suivant Y et Z. Le
transfert de chaleur dans la paroi étant en régime stationnaire, en mesurant les
températures à différents points suivant X et en les portant dans un graphe t=f(x),
nous constatons que la distribution de température est linéaire. La pente de la
t1t2
Fig.
1.
3
: Gradient de température
t+∆t ∆t t-∆t
n
t1>t2
∆
n
S
Q
t
1
=100°C
t
2
=0
°C
x
Fig. 1.4 : Schéma de l’expérience