MAGNETISME'

AERO 1
ELECTROMAGNETISME
I - Champ magnétique créé par un aimant
A - Les aimants
Les aimants naturels sont constitués d’oxyde magnétique de fer de formule Fe3O 4 .
Les aimants artificiels sont en acier ou en alliage et ont des formes variées : droits, en U, aiguille aimantée.
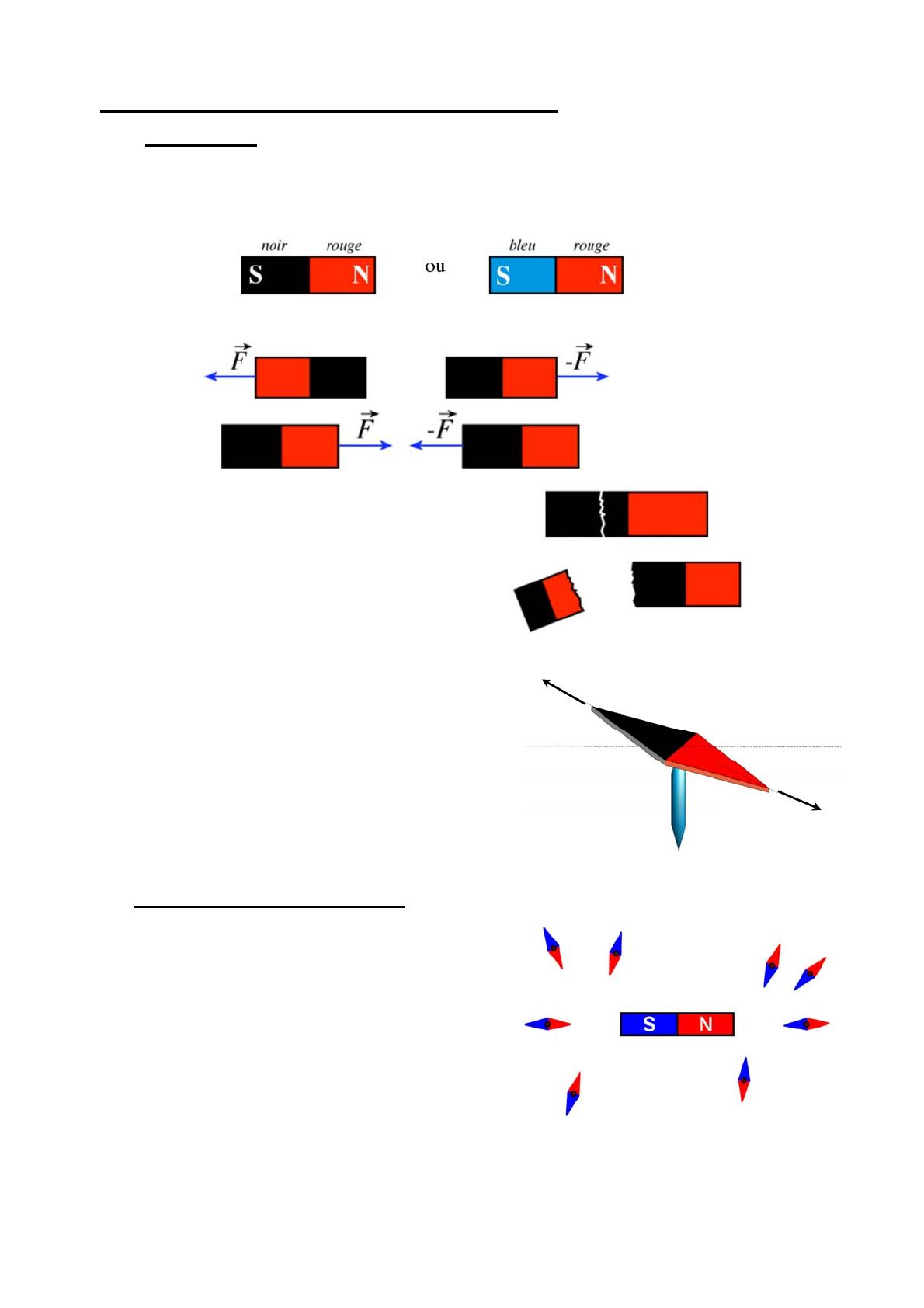
Les extrémités d’un aimant sont appelées pôle nord et pôle sud.
Deux pôles de même nom se repoussent, deux pôles de nom différents s’attirent.
Si on brise un aimant en deux, chaque morceau se
comporte comme un nouvel aimant : il est impossible
d’isoler le pôle nord du pôle sud d’un aimant.
Les aiguilles aimantées
En un point de la surface terrestre, une petite aiguille
aimantée mobile autour d’un axe vertical et éloignée de tout
aimant, de tout courant électrique et de toute masse
métallique comportant du fer, s’oriente toujours dans la
même direction et dans le même sens.
Par convention, on appelle pôle nord (en rouge) de l’aiguille
aimantée l’extrémité qui pointe approximativement vers le
nord géographique de la Terre et pôle sud, l’autre extrémité.
Sud géographique
S
N
Nord géographique
B - Notion de champ magnétique
Des aiguilles aimantées, placées en différents points du
voisinage d’un aimant droit prennent une direction et un
sens différents de ceux qui étaient initialement les leurs.
Les aiguilles aimantées subissent de la part de l’aimant une action qui diffère d’un point à un antre de
l’environnement de l’aimant.
La présence d’un aimant modifie les propriétés de l’espace qui l’entoure : on dit qu’il créé un champ
magnétique dans son environnement.
Caractéristique du champ magnétique :

On représente le champ magnétique créé par un aimant en un point P par une grandeur vectorielle B .
B
Point d’application : le point P
Direction : axe de l’aiguille aimantée à l’équilibre
Sens : Du pôle nord vers le pôle sud de l’aimant ( ou du pôle sud vers le pôle nord de
l’aiguille)
Intensité : B unité dans le S.I. le tesla (T)
P
Remarque : La valeur du champ magnétique peut être mesurée avec un teslamètre, appareil muni d’une
sonde à effet Hall
C - Spectres magnétiques et lignes de champs
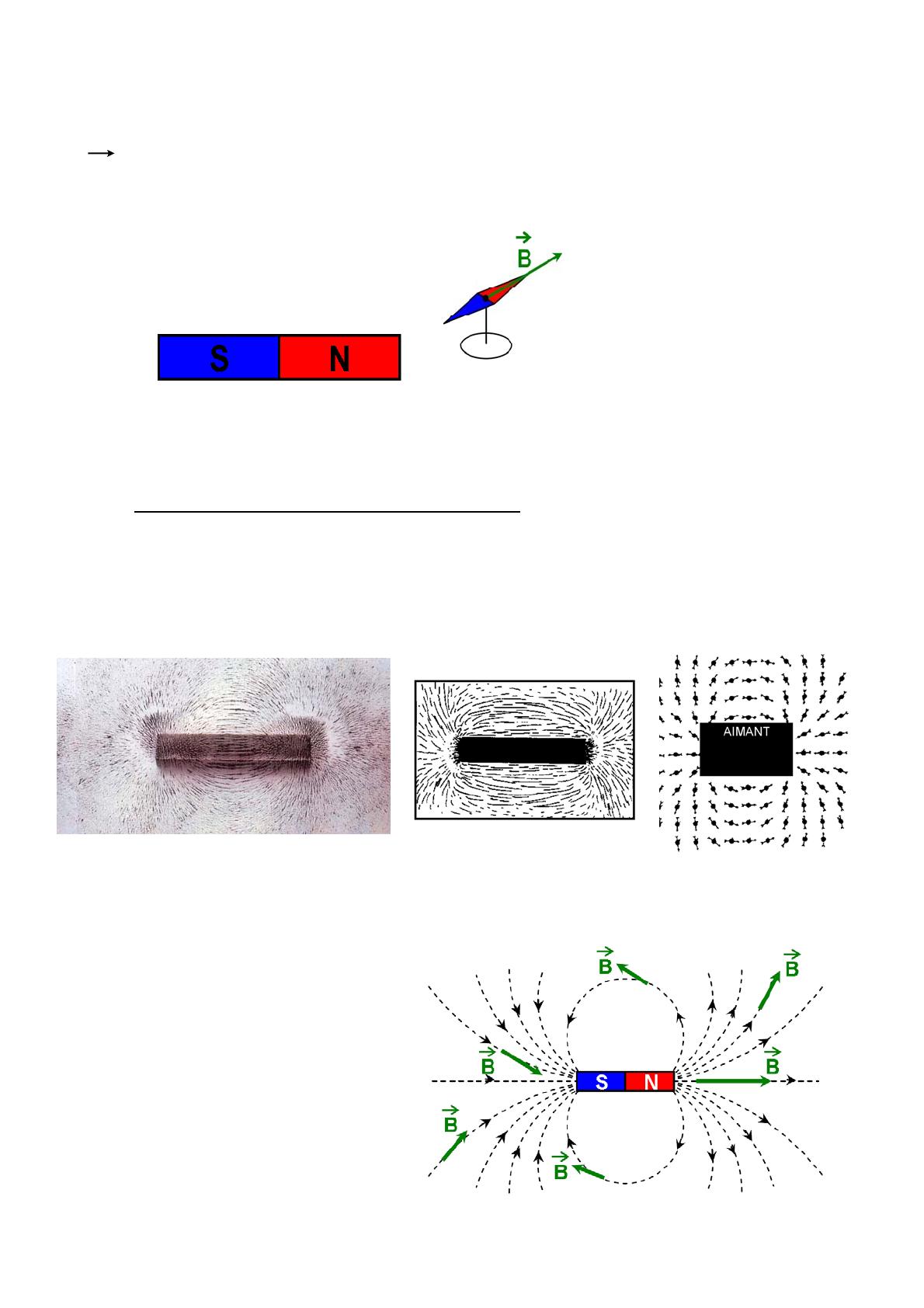
Réalisation d’un spectre magnétique
On saupoudre de la limaille de fer sur une plaque autour d’un aimant. Les grains de limaille de fer s’oriente
et dessine des lignes dans l’espace autour de l’aimant. On peut placer également des petites aiguilles
aimantées autour de l’aimant.
La figure ainsi formée est appelée spectre magnétique.
Interprétation : Chaque grain de limaille de fer s’aimante en présence du champ magnétique et se comporte
comme une minuscule aiguille aimantée en s’orientant.
La limaille de fer du spectre magnétique semble suivre des lignes appelées lignes de champ magnétique.
Lignes de champ
On appelle ligne de champ magnétique une
courbe en chaque point de laquelle le

vecteur champ magnétique B est dirigé
selon la tangente à cette courbe.
Une ligne de champ magnétique sont
orientées du pôle nord vers le pôle sur de
l’aimant.
Les lignes de champ sortent par le pôle
nord de l’aimant, entrent dans l’aimant
par le pôle sud.
- Les lignes de champ vont du pôle nord vers le pôle sud.
- Le champ B est tangent aux lignes de champs.
- Si on place une aiguille aimantée au point P, son pôle
nord va s’orienter dans la direction de B.
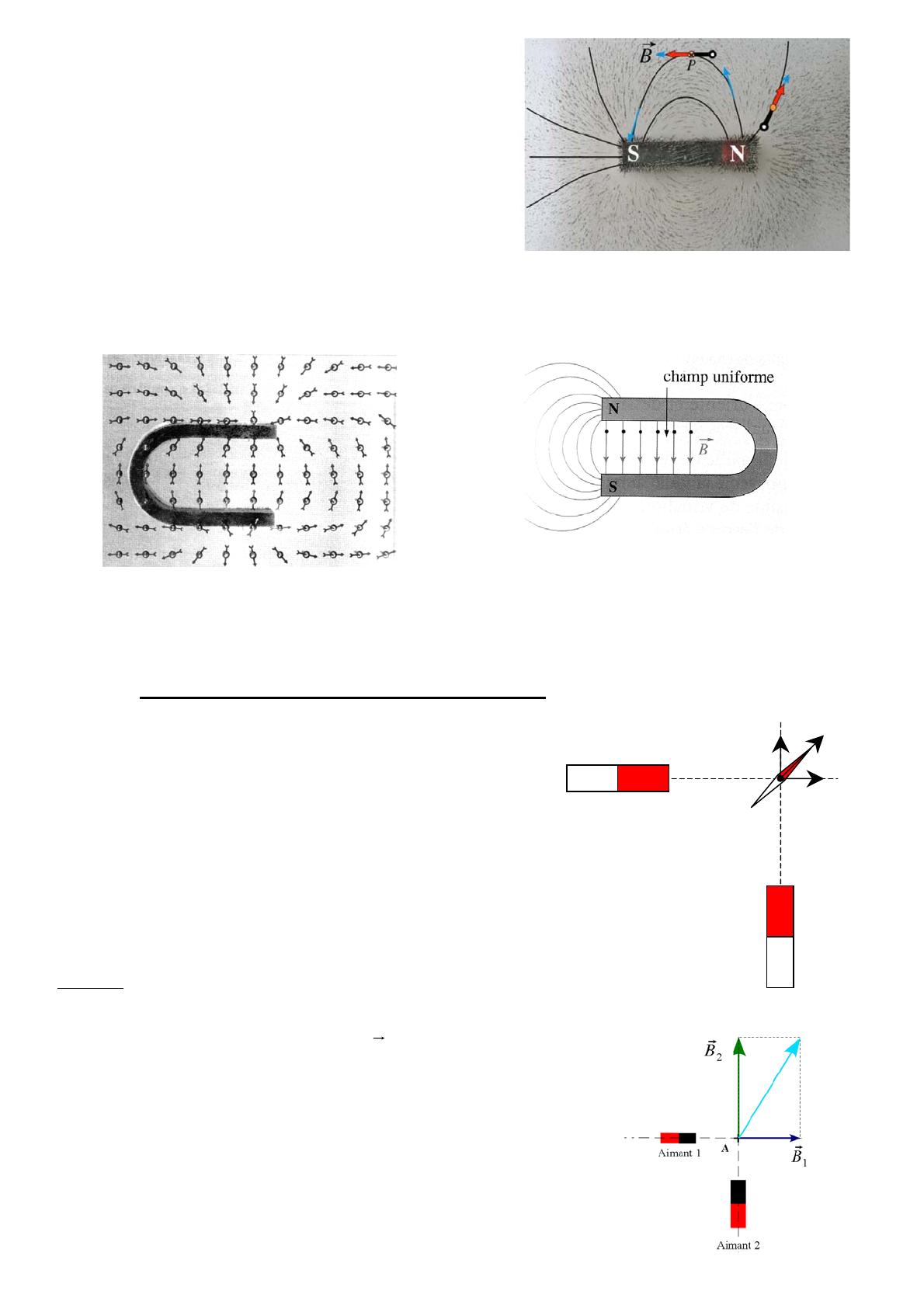
Champ magnétique uniforme
Entre les branches de l’aimant en U, les lignes de champ magnétique sont des droites parallèles : le champ
magnétique créé par l’aimant est uniforme.
Un champ magnétique est uniforme dans une région de l’espace si, en tout point de cette région, le

vecteur champ magnétique B a même direction, même sens et même valeur.
D - Superposition de deux champs magnétiques
En un point de l'espace, on peut faire agir plusieurs sources de
champs magnétiques. Le vecteur champ magnétique résultant en
ce point sera la somme des vecteurs champs magnétiques des
différentes sources magnétiques en ce point.
S
N

B1

Conclusion : Les champs magnétiques se composent de


manière vectorielle. Si deux champs B1 et B2 se superposent en

un point M, le champ magnétique B en ce point est leur somme
vectorielle.
  
B  B1  B2 .
Exemple : Deux aimants 1 et 2 créent individuellement au point
A des champs magnétiques perpendiculaires d'intensité
B1 = 30 mT et B2 = 50 mT.
Déterminer le vecteur champ magnétique B résultant au
point A. ( intensité et direction)

B

B2
N

S
E - Champ magnétique terrestre
La Terre possède un champ magnétique produit par les déplacements
de son noyau externe Le noyau externe est composé essentiellement de
fer et de nickel en fusion conducteurs - qui se comporte comme une
gigantesque dynamo.
L'effet dynamo est une théorie géophysique qui explique
l'origine du champ magnétique terrestre. Dans le mécanisme de
cette dynamo le mouvement liquide dans le noyau externe de la
terre déplace un matériau conducteur (fer liquide) et génère un
courant électrique.
Ce courant électrique produit un champ magnétique qui se
trouve le long de l'axe de la rotation de la terre.
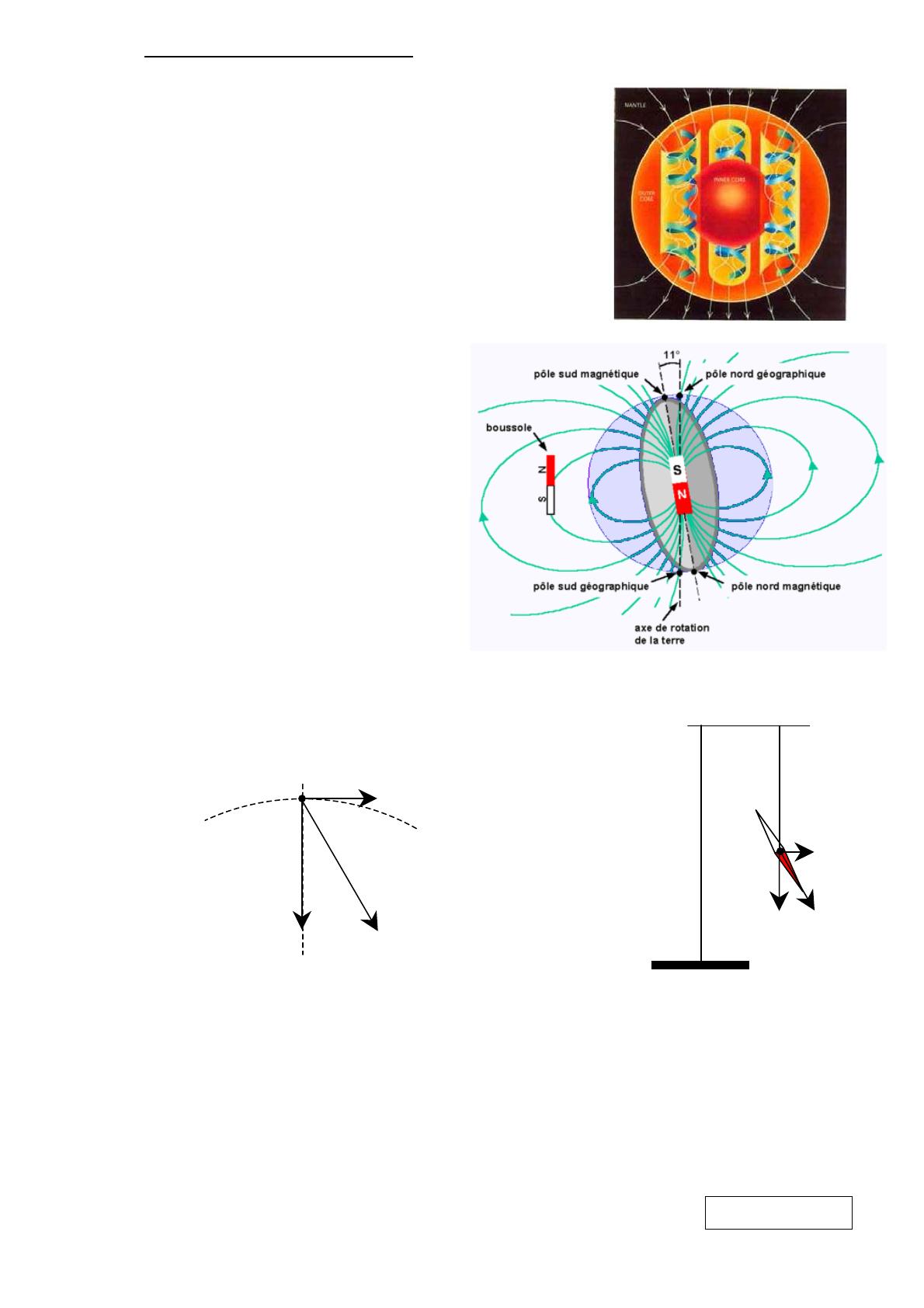
La Terre est une source de champ magnétique, on
peut la considérer comme un aimant droit.
Le pôle nord d’une aiguille aimantée s’oriente vers le
pôle magnétique de la Terre voisin du pôle nord
géographique, donc c’est un pôle sud magnétique.
Le champ magnétique terrestre assimilable en
première approximation, au champ que créerait un
aimant droit placé au centre de la Terre et incliné
d’un angle de 11° par rapport à l’axe des pôles
géographiques (angle = la déclinaison).
On suspend une aiguille aimantée, afin qu’elle soit libre de s’orienter dans le plan vertical et dans le plan

horizontal, la direction prise par cette aiguille est celle du champ magnétique terrestre BT .
Le champ magnétique terrestre plonge vers l’intérieur de la Terre.

BH
Surface de la
Terre

BV

BT
Vers le pôle
magnétique de
l’hémisphère nord

BH

BV

BT
Vers le centre
de la Terre


Le champ magnétique terrestre BT est la somme vectorielle de ses deux composantes horizontale BH

et verticale BV .
 
L’angle I  (BH ,BV ) s’appelle l’angle d’inclinaison, il varie au cours du temps et dépend du lieu. En
France il vaut environ 60°.
La valeur du champ magnétique terrestre varie selon le lieu en fonction de la latitude et des anomalies
magnétiques locales ( 30 μT à l’équateur magnétique et 60 μT aux pôles).
La valeur de la composante horizontale du champ magnétique terrestre est environ BH  2, 0 10
c’est à cette composante que les boussoles sont sensibles.
5
T,
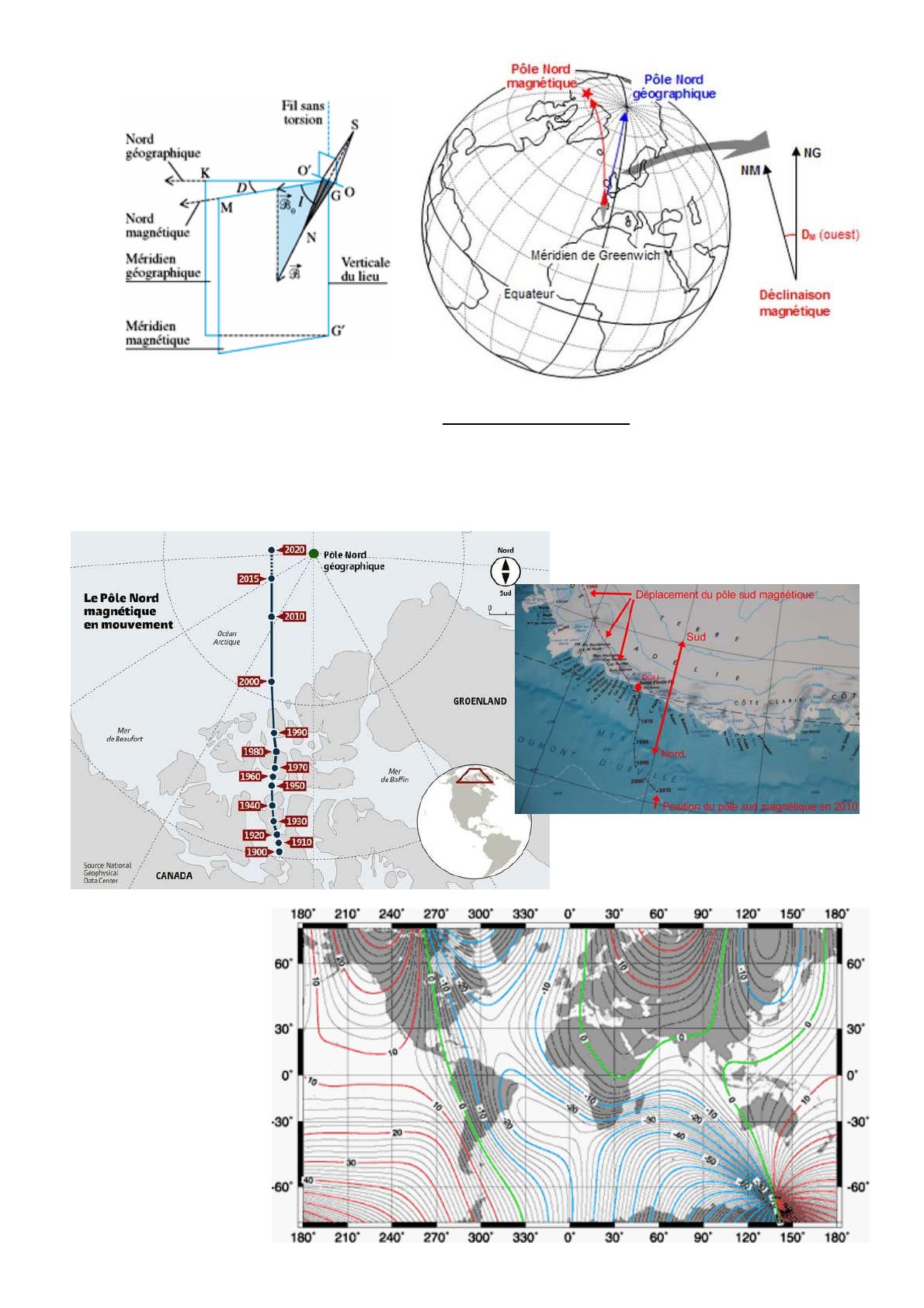
Angle de déclinaison magnétique D
En un point donné de la terre on appelle déclinaison magnétique D, l’angle entre la direction
du pôle nord géographique ( ou passe l’axe de rotation de la terre ) et la direction du pôle nord magnétique (
indiqué par la boussole
Les postions des pôles nord et sud magnétiques évoluent au cours des années ce qui modifie la déclinaison
magnétique en un point donné.
De plus la déclinaison
magnétique dépend du
lieux géographique
Carte des déclinaisons
magnétiques en 2010
II - Champ magnétique créé par un courant
A - Expérience d’Oersted (1819)
On place une aiguille aimantée au voisinage d’un fil de cuivre
rectiligne et horizontal. On fait passer un courant continu dans le fil
et on observe l’aiguille aimantée.
Lorsque le courant circule, l’aiguille aimantée
subit une déviation, elle se dispose
perpendiculairement au fil.
Si nous inversons le sens du courant, le sens
de l’aiguille s’inverse.
+
+



+
Un conducteur parcouru par un courant
électrique créé un champ magnétique dans son voisinage.
B - Champ magnétique créé par un courant rectiligne
Si l’on trace le spectre au voisinage
d’un fil rectiligne traversé paar un
courant I on constate que :
Lignes de champ :
Les lignes de champ magnétique d’un
courant électrique rectiligne sont des
cercles concentriques ayant pour axe le
fil transportant le courant.
Sens du champ :
Le sens du champ magnétique dépend du sens du
courant.
Il existe plusieurs règles pour déterminer le sens du
champs magnétique
Règles de l’observateur d’Ampère :
Un observateur, disposé le long du conducteur de façon que le
courant électrique circule de ses pieds vers sa tête, et regardant
vers un point A de l’espace, y voit le vecteur champ magnétique

B orienté par son bras gauche tendu.
Règle du tire bouchon :
Pour progresser dans le sens du courant, un tire bouchon doit
tourner dans le sens du champ.
Règle de la main droite :
I
I

B

B
Intensité du champ :
L’intensité du champ magnétique crée par un fil rectiligne en un point est proportionnelle à l’intensité du
courant électrique dans le fil.
En tout point M dont la distance par rapport au fil est r,
l'intensité du champ magnétique est
définit par la relation :
B valeur du champ en (T)
I intensité en (A)
r distance en (m)entre M et le fil
μ0 I

B(M ) 
μ 0  4π.10 7 u.s.i . perméabilité absolue du
2π r
vide
Exemple : Un conducteur électrique parcouru par un courant I = 500A produit à 10m autour de lui un
champ magnétique B =
C - Champ magnétique créé par un solénoïde
Un solénoïde est constitué par un enroulement en hélice de N
spires de fil de cuivre, régulièrement répartie sur la surface latérale
d’un support cylindrique dont la longueur L est grande par rapport à
son rayon.
Si un courant I traverse ces spires, il apparaît un champs
magnétique B au centre du solénoïde.
Lignes de champ :
A l’intérieur du solénoïde, les lignes de champ
sont parallèles.
A l’extérieur du solénoïde, les lignes de champs
ont la même allure que celle d’un aimant droit.
A l’intérieur d’un solénoïde et suffisamment loin
des extrémités, le champ magnétique est
uniforme et de même direction que l’axe du
solénoïde.
Faces d’un solénoïde :
L’analogie avec l’aimant droit suggère de définir une face sud et une face nord.
Une face nord d’un solénoïde est la face qui attire le pôle sud
d’une aiguille aimantée.
Les lignes de champ magnétique d’un solénoïde sont orientées
de telle manière qu’elles sortent du solénoïde par sa face nord
et entrent dans le solénoïde par sa face sud.
Reconnaissance des faces : On se place devant la face. La
lettre S ou N doit être fléchées dans le même sens que I.
Sens du champ :
Le sens du champ magnétique dépend du sens du courant.
Le champ magnétique à l’intérieur du solénoïde est dirigé de la face sud vers la face nord.
Règle de l’observateur d’ampère : c’est la même que
précédemment.
Règle du tire bouchon : c’est la même que précédemment
Règle de la main droite :
Si les doigts de la main (autres que le pouce) s’appliquent sur les spires du
solénoïde dans le sens du courant, le pouce tendu indique le sens du
champ magnétique sur l’axe du solénoïde.
Valeur du champ magnétique à l’intérieur d’un solénoïde :
B  μ0 n I  μ0
N
I
L
B valeur du champ en T
I intensité du courant en A
n nombre de spires par unité de longueur en m 1
μ 0  4π.10 7 u.s.i .
N nombre de spires
L longueur du solénoïde
Exemple : Calculer l'intensité B du champ magnétique dans une bobine longue ( 20cm , 400 spires )
traversée par un courant I = 16 A :
D - Champs magnétique créé par une bobine plate
Au centre O d'une bobine plate de N spires et de rayon R parcourue par un courant I, l'intensité B du
champ magnétique est donné par la relation :
Exemple : L'intensité du champ magnétique au centre d'une bobine plate ( 500 spires de
rayon R = 4cm ) parcourue par un courant I = 8 A est :
III - Ferromagnétisme
A - Vecteur excitation magnétique :
Si on considère un solénoïde rempli d’air, on sait
que le champs magnétique gréé en sont centre a pour
N
expression : B 0  μ 0   I
L
Les termes N, L et I dépendent de la source de champ
magnétique (la bobine).
Le terme μ 0 dépend du milieu qui se trouve au centre de la
(l’air ).
On définit le vecteur excitation magnétique
H
bobine
H qui ne dépend que de la source par : B 0  μ 0  H
 H est un vecteur colinéaire au vecteur champs d’induction magnétique B
 l’excitation magnétique H s’exprime en ampère par mètre A/m ou A.m-1
Remarques :
* Dans l’air ou dans le vide, la relation s’écrit
B0 = µ0.H avec µ0 = 4..10-7 (U.S.I.) = perméabilité
Magnétique du vide ou de l’air
Dans l’air ou dans le vide, le champ magnétique
est proportionnel à l’excitation magnétique.
pente : µ0
* Dans le cas d’un solénoïde plongé dans l’air, on
peut écrire : B0 = µ0.N.I / L et B0 = µ0.H
D’où : H = N.I / L
H=NI/L
 L’excitation magnétique s’exprime en effet en A/m
B - Milieux ferro ou ferrimagnétiques
Corps ferromagnétiques : corps cristallins pouvant être aimantés (Fer, cobalt, nickel et leurs
alliages,Fe3C). L’aimantation peut être grande et reste permanente en l’absence de champ extérieur. Compte
tenu de l’énorme augmentation des phénomènes magnétiques observée, les matériaux ferromagnétiques
présentent un intérêt fondamental en électrotechnique.
Corps ferrimagnétiques : cristaux (les ferrites) dont les propriétés magnétiques se situent
entre celles des anti-ferromagnétiques (qui ne peuvent être aimantés) et les ferromagnétiques
Une ferrite est une sorte de céramique obtenue par moulage à haute température (>1000°C)
et à haute pression (oxydes ternaires fer-cobalt, fer-nickel par exemple) Les ferrites ne sont pratiquement
pas conducteurs électriques ; ce qui les destine aux applications hautes fréquences.
Corps anti-ferromagnétiques : Exemples matériaux diamagnétiques : Cuivre, or, argent, zinc, plomb ,
silicium…et matériaux paramagnétiques : Aluminium, tungstène, platine, étain…Diamagnétisme et
paramagnétisme n’entraînent aucune propriété magnétique intéressante.
Action d’un milieux ferromagnétique sur les lignes de champs :
En présence d’un élément
ferromagnétique les lignes de
champ se concentrent pour passer à
travers le milieu ferromagnétique.
Explication : sous l’effet de B, le
corps ferromagnétique subit une
aimantation et crée un champ
magnétique qui s’ajoute au
premier. Le champ total est donc plus intense autour du corps ferromagnétique.
Noyau ferromagnétique à l’intérieur d’un solénoïde
Si on place un noyau en fer ou en ferrite au centre de la bobine , celui ci canalise les lignes de champ ce
qui a pour conséquence d’augmenter l’intensité du champ magnétique .
Le champ magnétique est renforcé par un facteur μr , appelé perméabilité relative du matériau.
B  r  0 
N
 i les valeur de μr sont comprises entre 100 et 20000 selon la qualité du noyau.
l
Conclusion :

Pour créer dans un matériau un champ magnétique B , il faut lui fournir une excitation magnétique notée

H . Champ magnétique et excitation magnétique sont liés par la relation :


B  μ  H  μr  μ0  H
avec µ : perméabilité magnétique du milieu
En intensité : B = µ.H
( B en T et H en A/m)
Perméabilité relative : on pose μ  μ r  μ 0
Perméabilité magnétique relative des matériaux
ferromagnétiques à 20 °C
Matériaux ferromagnétiques
Cobalt
µr (valeur maximale)
250
Fer
5 000
Mu-métal
20 000
Nickel
600
μ r est la perméabilité magnétique relative du matériaux
C - Courbe de première aimantation
Interprétation du phénomène d’aimantation
Un matériau ferromagnétique s’organise en petites
zones (dimension < 1mm), dites domaines de Weiss,
dans lesquelles existe une aimantation homogène.
L’orientation de ces aimantations étant aléatoire,
l’aimantation macroscopique moyenne est nulle.
Lorsqu’un tel matériau est soumis à une excitation H
croissante, les domaines de Weiss s’orientent
progressivement sur l’excitation, comme le montre la figure
ci-dessous :
Lorsque tous les domaines de Weiss sont orienté l’augmentation de H ne produit plus d’effet et on assiste
au phénomène de saturation.
L’évolution du champ B dans un tel matériau avec l’excitation H a ainsi l’allure suivante :
On distingue 3 zones :
A partir d’un état démagnétisé, la croissance de B suit
d’abord celle de H (zone linéaire) ;
l’augmentation de B s’infléchit ensuite pour se stabiliser
(zone de saturation)
Dans la zone de saturation, B augmente avec H de la
même façon que dans l’air. (droite en pointillés sur la
figure).
Le matériau étant initialement démagnétisé, la courbe
porte le nom de courbe de 1ère aimantation.
Ci-dessous : Courbes de 1ère aimantation de quelques substances ferromagnétiques courantes (à gauche) et
variation de leur perméabilité relative μR avec l’état magnétique (à droite).
D - Phénomène d’hystérésis
La figure représente l’évolution du champ B dans un matériau ferromagnétique soumis à une excitation
H(t) alternative.
Après la 1ère croissance de H (de 0 à 1), le
retour à 0 (de 1 à 2) laisse un
champ rémanent BR.
Il faut que H atteigne la valeur négative –HC
(de 2 à 3) pour que l’aimantation s’annule.
HC est l’excitation coercitive.
L’évolution de B se poursuit alors (de 3 à 4,
puis à 5, 6 et de nouveau 1…)
Le cycle d’hystérésis obtenu traduit le retard
de l’évolution du champ B sur l’excitation H.
Aspect énergétique :
Le cycle d’hystérésis correspond à une dépense énergétique, afin de modifier les domaines de
Weiss ; cette dépense est d’autant plus importante que le phénomène est important, c’est à dire que la
surface du cycle est grande.
De même, les pertes par hystérésis augmentent avec la fréquence de l’excitation.
Matériaux durs et matériaux doux
Les matériaux ferromagnétiques sont classés en
matériaux doux et durs,
selon la forme de leur cycle.
Légende : matériau doux
matériau dur
Matériaux doux :
* Cycle d’hystérésis étroit
* Champ rémanent Br et excitation
coercitive Hc faible
* Pertes par hystérésis faibles
* Ils s’aimantent et se désaimantent très facilement
On les utilise pour réaliser des circuits magnétiques de (moteurs, transformateurs, …)
Exemples d’alliages utilisés pour les tôles des transformateurs
Matériaux durs :
* Cycle d’hystérésis large
* Champ rémanent Br et excitation coercitive Hc importante
* Pertes par hystérésis importantes
* Ils s’aimantent et se désaimantent très difficilement
On les utilise pour réaliser des aimants permanents
Applications technologiques
IV - Actions et forces électromagnétiques
Préambule : représentation d’un vecteur perpendiculaire au plan de la figure
Vecteur entrant
dans la figure
Vecteur sortant
de la figure
A - Action d’un champs magnétique sur une particule chargée
1 - Déviation d’un faisceau d’électron dans un tube cathodique
Principe du tube cathodique ( tube de Braun) : A l'intérieur d'un tube où règne un vide poussé, se trouve un
canon à électrons, constitué d'un filament porté à incandescence et d'une anode munie d'un trou. L'anode est
portée à une tension accélératrice U > 0 par rapport au filament.
V
Un grand nombre d'électrons passent par le trou et forment le faisceau électronique se dirigeant en ligne
droite (en absence de forces) vers l'écran fluorescent. En heurtant l'écran à grande vitesse ( v ) les électrons y
produisent un spot lumineux.
N
S
Lorsqu'on approche un aimant droit du tube le spot est dévié sur l'écran par rapport à sa position initiale.
En maintenant l'aimant de sorte que le champ magnétique soit horizontal et perpendiculaire au faisceau
on observe que le spot est dévié verticalement
Si on inverse le sens des pôles de l’aimant on constate que la déviation s’effectue dans l’autre sens.
S
N
Conclusions :
Le faisceau électrique est constitué de charges en mouvement (les électrons). Comme les électrons
sont déviés si on approche un aimant, on conclut qu’une charge qui est en mouvement avec une
vitesse V dans un champ magnétique B subit une force magnétique.
2 – Force de Lorentz (1823-1928)
Si une particule chargée de charge électrique q se déplace à la vitesse v dans un champs magnétique B
Elle sera soumise à une force magnétique f m , dite force de Lorentz, égale au produit vectoriel de q. v et B
fm  q.v  B
 f m est perpendiculaire au plan formé par q. v et B
 Son sens est donné par la règle des trois doigts de la main
droite
 Son intensité vaut :
f m  f m  q  v  B  sin( qv , B )
o fm en newton (N)
o q en coulombs ( C)
o v en mètre par secondes (m.s-1)
o B en tesla (T)
Remarque : la force est maximale si q. v et B sont perpendiculaires
Application à la déviation du faisceau électronique
Les électrons sont pourvus d’une charge négative q  e  1,6.10 19 C par conséquent le sens du vecteur
q. v est opposé au sens du vecteur vitesse v
B
canon
v
Trajectoire
q.v
f
Ecran
— Si on approche le pôle nord de l’aimant du
côté gauche du tube, le spot se déplace vers
le bas .
— Si on approche le pôle sud de l’aimant du
côté gauche du tube, le spot se déplace vers
le haut .
3 – Application à l’effet Hall
Si un courant Io traverse un barreau en matériau
conducteur ou semi-conducteur, et si un champ
magnétique d'induction B est appliqué
perpendiculairement au sens de passage du courant, une
tension Vh, proportionnelle au champ magnétique et au
courant Io, apparaît sur les faces latérales du barreau.
C'est la tension de Hall (1879).
Les électrons sont déviés par le champ magnétique, ils on
tendance à se rapprocher de l’électrode inférieure (sur la
figure) et à s’éloigner de l’électrode supérieure. Il se crée
alors une dissymétrie de charges entre les deux électrodes
créant une différence de potentiel appelée tension de Hall.
Les capteur de hall sont utilisés pour mesurer les champs d’induction magnétiques.
On les utilisent aussi pour mesurer des courants électriques sans contacts directes donc en maintenant une
parfaite isolation galvanique. C’est le principe utilisé dans les pinces ampèremétriques.
Un fil conducteur traversé par un courant
crée autour de lui un champ magnétique
dont les lignes de champs sont des cercles
concentrique. On place autour du fil
conducteur un circuit magnétique constitué
d’un anneau en matériau ferromagnétique.
Celui ci va capter et canaliser les lignes de
champs. On intercale dans le circuit
magnétique une sonde de hall permettant de
mesure le champs créé. Celui ci étant
proportionnel à l’intensité , on mesure ainsi
le courant circulant dans le conducteur.
Circuit magnétique
B - Action d’un champs magnétique sur un courant, force de Laplace
1 – Rails de Laplace
Un conducteur mobile ( de longueur l )est placé sur deux rails horizontaux connectés à un générateur, et
dans le champ magnétique d'un aimant en U.
l
Lorsque le courant passe le conducteur mobile roule vers le gauche où vers la droite selon le
sens du courant et selon le sens du champ magnétique.
Interprétation :
Dans un modèle simplifié on peut considérer que le
courant électrique est constitué d’un nombre N
d’électrons libres qui se déplacent tous avec la même
vitesse v dans le sens opposé au sens conventionnel du
courant.
Ces électrons se déplacent donc dans un champ
magnétique B  v de sorte que chaque
électron est soumis à une même force de Lorentz.
fm  q.v  B
avec q = -e
Comme les électrons sont retenus par le métal, c'est le
conducteur tout entier qui est soumis à une force
F appelée force électromagnétique de Laplace. Cette
force est égale à la résultante des N forces de Lorentz qui
s'exercent sur les électrons
F   f m  N .f m  N .qv  B
Si  est la longueur de conducteur placé dans le
champs, la vitesse des électrons peut se définir par :

où Δt représente le temps mis par un électron
t

N .q
B
 B
pour parcourir  . On obtiens alors F  N .q
t
t
v
or N.q  Q représente la charge totale qui circule dans le conducteur durant Δt donc
avec I intensité du courant. Conséquence :
F  I .  B
N.q Q

I
t
t
2 – Loi de Laplace (Pierre Simon De Laplace 1749-1827)
Toute portion de conducteur de longueur l , placée dans un champs d’induction magnétique B et traversé
par un courant d’intensité I est soumis à une force FL dite force de LAPLACE
l
FL  I .l  B
 I : intensité du courant en (A)
 l : longueur de conducteur soumise au champs B en (m)
 I .l est le vecteur orienté selon le sens de I
 B : vecteur champs magnétique en (T)
 FL ; vecteur force de Laplace en (N)
 FL est perpendiculaire à
I .l et B
Le sens de FL est donné par la règle des trois doigts de la main droite.
Son intensité vaut :
FL  FL  I .l . B . sin( I .l , B )
3 – Applications de la force de Laplace
Moteur à courant continu
Une spire rectangulaire , traversée par un courant I, est placée dans un champs magnétique . Le gmps est
canalisé grâce au noyau ferromagnétique et devin radial au voisinage de la spire. Les bruns axiaux de la
spire sont donc soumis à ds forces de Laplace tangentielles. Il en résulte un couple moteur.
Un dispositif balai collecteur permet d’inverser le sens du courant à chaque demi tour et maintenir ainsi un
Couple constant.
Page 17/31
Définition légale de l’ampère :
Un fil (supposé infini)traversé par un courant crée
un champ magnétique (très faible), et l'autre fil
(infini) traversé par un courant est soumis au
champ magnétique du premier fil, il s'exerce alors
un force de Laplace (infime) sur le deuxième fil
qui va être attiré.
La réciproque est vrai; le deuxième fil crée lui
aussi un champ magnétique auquel est soumis le
premier fil.
L'effet est si faible, même avec des fils très fin, on
ne constatera aucun déplacement visible.
La définition de l'ampère de 1948 :
« Un ampère est l'intensité d'un courant
constant qui, s'il est maintenu dans deux conducteurs linéaires et parallèles, de longueurs infinies, de
sections négligeables et distants d'un mètre dans le vide, produit entre ces deux conducteurs une force
linéaire égale à 2 ×10−7 newton par mètre. »
V - Flux Magnétique
A - Flux magnétique à travers une surface fermée.
1 – Vecteur surface S
Soient :
• Un contour (C) ferme et oriente.
• Ce contour (C) forme une surface S.
On définit le vecteur surface S par :
• Sa norme : la surface S. en (m²)
• Sa direction : perpendiculaire a la surface S.
• Son sens : celui de la règle de la main droite ou la
règle du tire-bouchon.
• Son point d'application : le centre de la surface.
2 - Définition du flux magnétique à travers un contour fermé
On considère un contour (C) ferme définit
par son vecteur surface S .placé dans une
région de l’espace où règne un champ
magnétique B .
Le contour (C) est traverse par un certain
nombre de lignes de champ qu'on représente
par le vecteur B .
On définit le flux magnétique Ф par le produit
scalaire :
  B. S
soit :
  B.S . cos θ
Unité de flux : le wéber (Wb)
Avec : θ  ( B , S ) angle entre le champ B et le vecteur surface S
B intensité du champs magnétique en tesla (T)
S surface du contour en (m²)
Page 18/31
Exemple : calculer le flux à travers une spire circulaire de rayon R = 5 cm placé dans un champs
d’intensité B = 0,4 T dans les cas suivants :
θ (°)
0°
45°
90°
180°
Φ (Wb)
Le signe du flux magnétique Ф dépend du sens de parcours du contour (C) définit de façon
arbitraire. En ce qui concerne le flux magnétique, ce qui est important c'est la valeur absolue du
flux.
On remarque aussi que la valeur de Ф dépend de l'angle θ. Le flux Ф sera maximal pour les
valeurs θ = 0 ou θ = π.
3 - Flux à travers un bobine comportant N spires :
  N .B. S
  N .B. S . cos θ
B - Conservation du Flux Magnétique
On appelle tube de champ l'ensemble des lignes de champ contenue dans un contour fermé (C).
Le flux magnétique se conserve dans un même tube de champs,
on dit que le flux est conservatif.
Conservation du flux à travers un tube de champ : le flux à travers le contour (C1) et égal au flux à
travers le contour (C2) car ceux-ci s'appuient sur le même tube de champ et embrassent le même nombre de
lignes de champ. Donc   B1 . S1  B2 . S 2
Comme S 2  S 1 on en déduit que B 2  B1
Page 19/31
Exemple de tube de champs dans un circuit ferromagnétique
matériau ferromagnétique
S2
Entrefer
S1
Le cadre ( appelée carcasse) construit dans un matériau ferromagnétique ( fer au silicieum) canalise
les lignes de créées par la bobine. La réduction de la section (S2 << S1) permet d’obtenir dans l’entrefer un
champs magnétique très intense ( B2 >> B1)
C - Règle du Flux maximum
Considérons une bobine suspendue à un fil et alimentée par un courant continu. Lorsque l'on présente par
son pôle Nord un aimant droit devant cette bobine, celle-ci pivote (a) pour venir se placer tel que le pôle Sud
de la bobine soit devant le pôle Nord de l'aimant (a). Ensuite la bobine de rapproche de l’aimant (b) de telle
sorte que le maximum de lignes de champs traverse celle ci. On remarque au final que le flux magnétique
créé par l'aimant et embrassé par la bobine est maximal : l'angle θ entre le champ de l'aimant et le vecteur
surface de la bobine est nul .
Règle du flux maximum : Tout conducteur parcouru par un courant , délimitent une surface elle même
orientée par le sens du courant, et placée dans un champ magnétique tend a s'orienter de façon a ce que le
flux au travers de la surface soit maximum (en valeur absolue et positif).
Cette règle est une autre forme de la loi de Laplace car ce sont des forces électromagnetiques qui agissent
sur le conducteur pour l'orienter.
Page 20/31
VI - Induction
A - Force électromotrice induite
1 – Mise en évidence
si on remue un aimant devant une bobine, non alimentée, on observe une tension à ses bornes.
• Si on approche l'aimant vers la bobine, l'aiguille du voltmètre dévie dans un sens.
• Si on approche l'aimant vers la bobine plus rapidement, l'aiguille du voltmètre dévie dans
le même sens et de façons de plus importante
• Des que le mouvement de l'aimant s'arrête, le voltmètre affiche 0.
• Si on éloigne l'aimant de la bobine, l'aiguille du voltmètre dévie dans l'autre sens.
Interprétation :
• Lorsque l'aimant est en mouvement, on observe une tension aux bornes de la bobine : la
bobine se comporte comme un générateur.
• Si le mouvement de l'aimant cesse, la tension aux bornes de la bobine est nulle : la tension
aux bornes de la bobine existe s'il y a une variation de mouvement.
• Lorsque l'aimant se déplace, la bobine embrasse un flux magnétique qui varie suivant la
position de l'aimant : la bobine est soumise a un flux variable.
• Plus l'aimant se déplace rapidement, plus la tension aux bornes de la bobine est important.
phénomène de l'induction électromagnétique
Pour tout circuit soumis a une variation de flux magnétique, il se crée a ses bornes une
tension. Force électromotrice induite ( f.e.m. induite) qui est proportionnelle au variations
du flux. Le circuit se comporte alors en générateur. Cette fem est notée e et s’exprime en volt.
2 – Loi de FARADAY
e(t )  
d
dt
On écrit aussi :
f.e.m. induite = e(t )  

variation de flux
=
 vitesse de variation du flux
t
durée
Page 21/31
Vocabulaire :
- on appelle inducteur la source de champ magnétique.( ici l’aimant )
- on appelle induit le circuit ou l’élément aux bornes duquel apparaît la fém induite.( bobine)
 
Le flux s’exprime :   N  B  S  cos( B  S ) ,pour obtenir variation de flux il faut :
- Soit faire varier le champ B (transformateur)
 
- Soit faire varier l’angle ( B , S ) ( alternateur)
-
Soit faire varier la surface S (c’est le cas suivant)
2 - Déplacement d’un conducteur dans un champ uniforme

Déplacement d’une tige dans un champ B uniforme (aimant en U)
Aimant
Voltmètre

v
B
V
Rails
K
tige mobile instant t2
tige mobile instant t1
- Quand le conducteur est déplacé, une fém induite est créée.
- L’amplitude de la fém induite augmente avec la vitesse de déplacement.

- Le signe de la fém induite varie avec le sens de B et le sens du déplacement.
Interprétation : Lors de son déplacement, le conducteur coupe les lignes de champ .La surface S du circuit
augmente : Une fém induite e apparaît.
Expression de la fem induite:
l
x
La tige durant de longueur l se déplace entre les instants t2 et t1 d’une longueur x, ce qui augmente la
surface coupée par le champs magnétique B de S  l . x . Ce qui provoque une augmentation de Flux de
  B .S  B .l . x . Si l’opération s’effectue durant l’intervalle de temps t  t 1  t 2 , la f.e.m. induite
s’exprime par : e  

B .l . x
x
x

  B .l 
  B .l .v en posant v 
vitesse de la tige
t
t
t
t

La fém induite dans un conducteur de longueur l en déplacement dans un champ B uniforme
est proportionnel à la vitesse v de son déplacement.
e  B .l .v
 

si B  v et B  l
Page 22/31
Application : fem induite dans une machine à courant continu
Un machine à courant continu est constituée de conducteurs rectilignes ( au niveau de rotor) qui se
déplacent dans un champs magnétique créé par les aimants du stator. Ils coupent en permanence le flux
magnétique et sont le siège d’une fem induite.
Il apparaît aux bornes du collecteur une fem induite proportionnelle au flux et à la vitesse de rotation.
C’est le principe de la génératrice : e  k ..
3 - Principe de l’alternateur
les bobinage induits sont fixes et disposés sur le
stator, l’inducteur est constitué d’un aimant qui (rotor)
qui tourne au centre des bobines. Le flux induit dans
les bobines varie sinusoidalement du fait que l’angle θ
entre champs et vecteur surface varie en permanence
de 0 à 2π.
  N .B. S . cos θ
Si on pose que θ  ω.t avec ω vitesse angulaire de
rotation alors ( t )  N .B. S . cos(ωt )
Le flux est donc une fonction sinusoïdale du temps
En appliquant la loi de Faraday :
d ( t )
d cos(ωt )
e( t )  
  N .B. S
  B . S .ω. Sin(ωt )
dt
dt
La fem induite dans chaque bobine est une
grandeur sinusoïdale dont l’amplitude est proportionnelle à la vitesse de rotation.
Remarque : si les bobines sont décalées de 2π/3 on obtient un système de 3 tensions triphasées.
4 – Principe du transformateur
On fait circuler un courant alternatif dans la bobine du
primaire. Cette bobine crée un champ variable dont les
lignes de champ sont canalisées par la carcasse appelée
circuit magnétique.
La bobine du secondaire, soumise au flux variable voit
apparaître un fém induite à ses bornes.
Un transformateur est un convertisseur d’énergie
permettant de baisser ou d’élever une tension. Il permet
également d’isoler deux circuits électriques
Page 23/31
B - Courant induit
1 – Loi de Lenz
On déplace un aimant devant une bobine fermée sur un ampèremètre, on constate l’apparition d’un
courant induit dont le sens dépend du sens de déplacement du champs
- Si on approche le pôle Nord de l’aimant : Le sens du courant i, crée un pôle Nord s’opposant à
l’approche du pôle Nord de l’aimant.
- Si on éloigne le pôle Nord de l’aimant : Le sens du courant i, crée un pôle Sud s’opposant à
l’éloignement du pôle Nord de l’aimant.
- Si on approche de la bobine le pôle Sud de l’aimant : Le sens positif du courant i, crée un pôle Sud
s’opposant à l’approche du pôle Sud de l’aimant.
- Si on éloigne le pôle Sud de l’aimant : Le sens du courant i, crée un pôle Nord s’opposant à
l’éloignement du pôle Sud de l’aimant.

Conclusion : La variation du champ B entraîne la circulation d’un courant induit. Ce courant crée à son
tour un champ magnétique qui s’oppose à la cause qui lui a donné naissance, c’est-à-dire la variation

de B .
Enoncé de la loi de LENZ :
Le courant induit, par ses effets, s’oppose à la cause qui lui a donné
Conséquence : La loi de Lenz permet d'orienter la f.e.m. e(t) en convention générateur.
Sur les schéma on considère que l’ampèremètre est récepteur et la bobine génératrice de fem e
e(t)
Ф augmente donc e(t) est négative
Ф diminue donc e(t) est positive
C - Courants de FOUCAULT (Léon Foucault 1851) Eddy currents
Si l’on approche une bobine alimentée par un courant
alternatif d’une masse de métal conducteur, le flux
alternatif produit induit dans la masse métallique des
courants électriques circulaire
Les courants de Foucault sont des courants
induits qui circulent dans la masse d’un conducteur.
Ils obéissent à la loi de Lenz donc s’opposent à la
variation du flux inducteur
Page 24/31
Les courants de Foucault prennent naissance de deux manière :
 Le conducteur est en mouvement devant un champ
magnétique fixe .Les courant de Foucault créent des force de
Laplace qui s’opposent selon la loi de Lenz au mouvement.
C’est le principe du freinage par courant de Foucault ou des
moteur à induction (moteurs asynchrone
 Le conducteur est fixe dans un champ magnétique variable. Le plus souvent ce champs est créé
par une bobine alimentée par un courant sinusoïdal. Si le conducteur est résistif , les courants de
Foucault provoque par effet Joule son échauffement. C’est le principe du chauffage par induction.
Ce phénomène est aussi la cause de l’échauffement donc de la perte pertes d’énergie dans les
machines électrique et les transformateur. (pertes par courant de Foucault)
Exemples d’application :
 Freinage par induction
Principe, un disque métallique entre deux bobinages alimentés sur commande par un courant continu .
Les le métal du disque coupe en permanence le flux des bobine ce qui provoque l’apparition de courants de
Foucault qui en accord avec la loi de Lenz provoque un couple résistant qui a tendance à freiner le disque.
Ce type de freinage est utilisé dans certains véhicule ( camion, train) . Cependant le couple de freinage
diminue avec la vitesse et est donc inefficace à basse vitesse. On les nomme ralentisseur à induction.
Remarque : Pour les train on utilise aussi un freinage linéaire où des bobines fixées aux bogie induise
directement les courants dans le rail
 Chauffage par induction
Principe, un bobinage inducteur alimenté par un
courant alternatif de fréquence élevé (>20kHz) entour la
pièce métallique que l’on veut chauffer. Les courants induits
dans la pièce provoquent par effet joule son échauffement.
Ce procédé est particulièrement efficace si le métal à
chauffer est très résistif (fer, acier)
Page 25/31
Application dans de nombreux domaines , frittage, frettage, forge, traitement thermique de surface,
soudage-brasage, inclusion de métal dans les plastiques, polymérisation des matériaux etc..
 Réduction des courants de Foucault
Les courants de Foucault peuvent être nuisibles, provocant des échauffements des tôles des
machines électriques à courant alternatif sinusoïdal et les transformateurs. Pour remédier à ces
effets les noyaux sont construits au moyen d’empilement de tôles minces séparées par un vernis
isolant. Ces feuilles sont faites d’un acier au silicium à grande résistivité. Les tôles sont rivetées
ensembles et isolées électriquement entre elles. Les courants induits sont ainsi de plus faible
intensité
 Phénomène de lévitation magnétique
On utilise des Céramique supra-conductrice qui ont la propriété d’avoir une résistivité nulle en
dessous d’une certaine température( inférieure à –140°C). Pour cela il faut les refroidir dans de
l’azote liquide (te = - 196°C).
Si on place un aimant au dessus d’une pastille de céramique
préalablement refroidie le phénomène de lévitation.
L’aimant tient en suspension au-dessus de la céramique du fait de
l’apparition d’un courant induit dans celle ci qui provoque un champ
magnétique qui s’oppose à l’aimant.
Page 26/31
VII - Auto-Induction
A - Inductance propre d’une bobine
Flux propre d’une bobine : Cas d’un solénoïde

S
Rappel : une bobine traversée par un courant I
Crée en son centre un champ magnétique
N
d’intensité B  μ 0 I
l

Ce champ crée lui même à travers les surfaces S
des N spires un flux   N  B  S appelé flux propre de la bobine
μ N 2S
N
Pour un solénoïde   N  μ 0 I  S  0
 I dépend que de la géométrie de la bobine et est
l
l
proportionnel à l’intensité I
Inductance propre d’une bobine : On pose
  L I
Dans le cas du solénoïde à aire L d’exprime donc par : L 
avec L inductance en Henry (H)
μ0  N 2  S
l
Exercice : Calculer l’inductance L d’un solénoïde de longueur 10cm de diamètre d=2cm et comportant 500
spires.
μr  μ0  N 2  S
Solénoïde avec noyau ferromagnétique : l’inductance devient L 
l
avec μ r permittivité relative du matériau ferromagnétique
B - Expression de la f.e.m. d’auto-induction
Si une bobine ,d’inductance L, est parcourue par un courant d’intensité variable i(t), elle est alors traversée
par un flux propre lui même variable Ф(t) = L.i(t)
Cette variation de flux entraîne l’apparition d’une force électromotrice d’auto induction e(t)
régie par la LOI de FARADAY e( t )  
d ( t )
dLi ( t )
di ( t )

 L
dt
dt
dt
La f.e.m. d’auto-induction est donc proportionnelle à la vitesse de variation de l’intensité
C - Relation entre courant et tension aux bornes d’une bobine
Considérons une bobine idéale de résistance nulle,
Si on lui applique une tensio uAB elle sera traversée par
Un courant i pris avecla convention récepteur.
La fem d’autoinduction dont le sens est donné par la loi
de Faraday est donc opposée à u (convention générateur)
di 
di

On a donc u AB   e    L    L 
dt 
dt

Page 27/31
u
di
dt
Loi d’Ohm aux bornes d’une bobine idéale :(inductance pure)
La tension u(t) aux bornes d’une bobine est proportionnelle à la variation de courant par rapport au temps.
L’inductance L est le coefficient de proportionnalité.
On a :
di
u  L
dt
L : inductance propre en Henry ( H )
i: intensité en Ampères ( A )
t : temps en secondes ( s )
u : tension en Volts ( V )
avec :
Remarque : Le signe de u dépend du sens de variation de i.
- Si i augmente, u > 0
- Si i diminue, u < 0
Cas d’une bobine réelle : (comportant une résistance non négligeable)
On tient compte de la résistance r
du bobinage du fil de cuivre
Le modèle équivalent de la bobine est
Composé d’une inductance pure L en série
avec une résistance r on écrit :
u  uL  ur  L
di
 ri
dt
D - Energie électromagnétique emmagasinée par une bobine
Une bobine peut stocker de l’énergie et la restituer pendant un temps très court (exemple
étincelle). Cette énergie s’exprime en fonction de l’intensité du courant par :
W
1
L. I 2
2
avec:
W énergie en Joule (J)
L inductance en Henry (H)
I intensité en ampère (A)
Démonstration : La puissance p est la dérivée de l’énergie W mais aussi le produit de la tension u par
di
dW
 u.i  L   i soit en simplifiant par dt : dW  L.i .di
l’intensité i donc p 
dt
dt
i2
En intégrant cette expression on obtient : W   dW  L. i .di  L 
2
E - Comportement d’une bobine en régime variable
L’inductance pure est une source de tension :
di
dt
- en régime établi et continu : la tension aux bornes de L est nulle u = 0
- en régime périodique établi : la valeur moyenne de u est nulle
- en régime quelconque : le courant ne peut pas subir de discontinuité
les trois conséquences de l’équation u  L.
Page 28/31
Rupture de courant dans un circuit inductif
Une brève variation de courant, comme par exemple l’ouverture d’un circuit, peut provoquer une variation
di
quasi infinie. Cela provoque aux bornes de la bobine une
dt
surtension brève u  L 
di
pouvant atteindre plusieurs
dt
Arc électrique
millier de volts. Cette surtension est à l’origine d’étincelles
d’extra rupture pouvant détruire les circuits.
Il ne faut jamais interrompre brutalement le courant dans
un circuit inductif.
Rôle de la diode de roue libre DRL
À la fermeture de l’interrupteur K,
la DRL est bloquée.
À l’ouverture, la DRL permet
d’écouler le courant,
évitant l’arc d’extra-rupture et
protégeant ainsi l’interrupteur K.
Conclusion : Une bobine s’oppose toujours aux variation brutales de courant.
Cette propriété est utilisée pour le lissage du courant dans les applications nécessitant un forte intensité
comme les alimentation ou les hacheurs.
Exemples de bobines de lissage :
En sortie d'un montage redresseur, si l'on souhaite avoir un courant le plus constant
possible, il faudra ajouter une bobine en série avec la charge.
Page 29/31
VIII - Application au Contrôle Non Destructif
Contrôle par flux de fuite magnétique (Magnétoscopie)
Le contrôle par flux de fuite magnétique consiste à soumettre la pièce ou une partie de celle-ci à un champ
magnétique constant. Les défauts superficiels provoquent, par l’importante variation de réluctance qu’ils
représentent, une déviation des lignes de champ. Des flux de fuite magnétique sont engendrés localement.
Ils sont ensuite généralement visualisés soit à l’aide d’un produit indicateur porteur de limaille de fer
(magnétoscopie), soit à l’aide d’un film magnétisable (magnétographie), soit à l’aide d’appareils de mesure
de champ magnétique.
Page 30/31
Contrôle par courants de Foucault
Cette technique utilise des courants induits à l’intérieur de la pièce,. Pour ce faire, un excitateur externe est
employé, souvent constitué d’une bobine parcourue par un courant alternatif. Les courants induits, parce
qu’ils forment des boucles et sont à la même fréquence que le courant d’excitation, engendrent un champ
magnétique alternatif de réaction sortant de la pièce à inspecter. Les défauts superficiels dévient les lignes
des courants de Foucault, et par suite modifient le champ magnétique résultant. La variation du champ
magnétique est enfin mesurée au moyen d’un élément sensible au champ magnétique alternatif, qui peut être
une bobine ou un capteur de champ magnétique.
L’utilisation des courants de Foucault dans les applications de CND est limitée aux pièces électriquement
conductrices. Elle s’étend de l’inspection des tubes (échangeurs, générateurs de vapeurs de centrales
nucléaires) à la recherche des défauts débouchant sur des surfaces plus ou moins planes. La principale
difficulté est la faible pénétration des courants induits, selon l’effet dit « de peau », qui rend difficile la
détection de défauts enfouis. C’est une technique sans contact et la rapidité d’établissement des courants
induits donne la possibilité de déplacer très rapidement la sonde.
Page 31/31