Cartographie l2

I. GENERALITES
Une carte géologique est la représentation sur un fond topographique des terrains qui affleurent à la
surface du globe ou qui ne sont cachés que par une faible épaisseur des formations superficielles
récentes dont on ne tient pas compte (éboulis, alluvions, sols et altération superficielle). La
cartographie géologique en Géoscience 2 envisage :
- la reconnaissance des structures ;
- la construction des coupes géologiques ;
- le commentaire des cartes géologiques.
I.1. NOTION ET TYPES DE STRUCTURES
A l’échelle cartographique, la structure d’une région désigne l’agencement des terrains (couches) les
uns par rapport aux autres. En pays sédimentaires, les types de structures sont déterminés par
l’évolution stratigraphique ou tectonique.
I.1.1. Structures liées à la tectonique (Figure 1).
- Structure monoclinale (S-L)
Elle englobe la structure tabulaire et la structure monoclinale au sens strict. Dans la structure
tabulaire, les terrains sont disposés en couches horizontales. Dans la structure monoclinale, les
terrains ont subi un basculement d’ensemble plus ou moins important, ils sont alors inclinés du
même côté.
- Structure plissée
Les terrains initialement horizontaux ou basculés ont subi dans les zones instables de l’écorce
terrestre des compressions, il en résulte après torsion des déformations sous forme d’ondulation
appelées plis.
I.1.2. Dispositions liées à la stratigraphie
Elles représentent des ensembles de terrains d’âge différents (chaque ensemble étant constitué de
terrains concordants) séparés par un contact normal et on distingue :
- des transgressions-régressions ;
- des discordances.
En pays des roches cristallines, les structures des terrains sont complexes et régies par la
zonéographie (En géologie, désigne une reconnaissance et une représentation d'un volume de terrain ayant un
certain degré de métamorphisme. Elle permet d'effectuer des classifications, dans l'espace, du métamorphisme).
En général, les terrains plutoniques aux limites plus ou moins régulières recoupent les terrains
encaissant ou se moulent à leurs structures. Les coulées (épanchement de magma) ou projection

volcaniques peuvent être concordantes ou discordantes sur les terrains sur lesquels elles sont
épanchées. Il est à noter que les contacts anormaux (faille, chevauchement, charriage) peuvent
affecter n’importe quel type de structure.
Figure 1 : Structures liées à la tectonique
1.2. PROPRIETES GEOMETRIQUES DES COUCHES
1.2.1. Notion de pendage
La géométrie d’un plan (couche géologique) est déterminée par deux paramètres :
Le pendage : c’est l’angle dièdre d’une couche (ou d’une faille) avec un plan horizontal h. C’est
l’angle (β) entre le plan horizontal et la ligne de plus grande pente (Lpp) du plan de stratification.
La valeur (β) varie de 0° à 90°. Il faut noter que pour une direction donnée, on a deux plans qui
présentent la même valeur de pendage mais présentent des sens du pendage (sp) opposés (Figure
2). Le pendage est dit réel lorsqu’il est mesuré perpendiculairement à la direction de la couche. Il est
dit apparent lorsqu’il est mesuré dans une position intermédiaire et est compté entre 0 et le pendage
réel. Dans ce cas, la mesure est faite parallèle à la direction de la couche et l’angle est nul.
La direction : c’est la valeur angulaire (α) que fait avec le nord, une ligne horizontale tracée dans le
plan de stratification de la couche (P). La valeur (α) varie de 0° à 180°.
Structure tabulaire
Structure monoclinale
Structure plissée

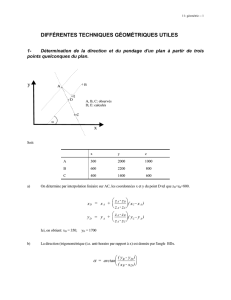
I.2.2. Représentations de la direction et du pendage : un plan est représenté sur une carte par des
signes conventionnels, généralement en (T) dont la barre horizontale est parallèle à l’horizontale du
plan et la barre verticale à sa ligne de plus grande pente. La longueur de cette dernière est
inversement proportionnelle à la valeur du pendage. Parfois le signe reste le même, mais on note, à
côté de lui, la valeur du pendage en degrés (figure 2).
I.2.3. Détermination du sens de pendage
Le pendage peut être déterminé de façon qualitative ou quantitative
I.2.3.1. Evaluation qualitative du pendage
a) A l’aide des signes conventionnels (Figure 4)
On utilise des signes conventionnels en forme de T comprenant une barre horizontale parallèle à la
direction et une barre verticale parfois fléchée orientée dans le sens du pendage. Ces signes peuvent
varier. La valeur du pendage ne peut excéder 90°. Les pendages horizontaux et verticaux sont
indiqués par des signes spéciaux :
Figure 2 : Pendage d’une couche

Figure 3 : Orientation d’un plan dans l’espace
Figure 4 : Représentation des directions de pendage sur une carte géologique
N.B : Les signes de pendage ne s’appliquent pas aux failles
b) A l’aide de l’intersection des couches avec la surface topographique (Figure 5)
On distingue trois cas :
 si la couche est horizontale, ses limites sont parallèles aux courbes de niveau
 si la couche est verticale, ses limites traversent de manière rectiligne les courbes de niveau
quelque soit le relief
B
A
a
B
A
b

 si la couche est inclinée avec notamment un angle compris entre 0 et 90°, les limites se
rapprochent d’autant plus de la formation des courbes de niveau qu’elles le sont de
l’horizontale.
Figure 5 : Evaluation du pendage à l’aide de l’intersection des couches avec la surface
topographique
Au niveau des collines et des vallées, elles ressemblent à un V appelé V topographique d’allure
curviligne. Pour obtenir le pendage, il faut observer l’intersection en forme de V d’une couche avec
la vallée, ensuite projeter sur le profil topographique trois points A, B et C à partir de cette
intersection. A se trouve à la pointe du V, B et C se trouve symétriquement à la même altitude sur
des flancs opposés de la vallée. Ceci suppose que les formes de terrains présentent des
dénivellations (vallées) ; les affleurements doivent être symétriques par rapport au tracé de la vallée
si les flancs de celle-ci ont des pentes voisines.
 Si le pendage est contraire à la pente de la surface topographique, la couche dessine dans le
talweg un rentrant dont la pointe indique le sens du pendage. Ce rentrant est moins accentué
que celui des courbes de niveau. Le point A correspondant à la pointe du V se trouve à une
altitude inférieure à celle de B et C.
B
A
c