problème sur le losange corrigé

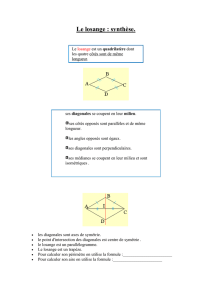
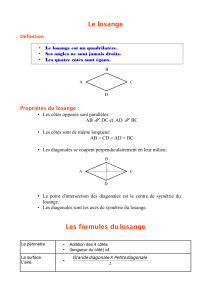
1
Devoir en temps libre : autour du losange
Ce problème contient trois exercices indépendants et de difficulté croissante sur le
thème du losange.
On démontrera notamment à l’aide des nombres complexes quelques résultats de
géométrie bien connus depuis le collège. A priori on ne s’autorise que les résultats
proprement démontrés dans le cours de CPGE ; lorsqu’un théorème vu dans le cycle
secondaire sera nécessaire, l’énoncé le précisera explicitement.
On définit un losange comme un quadrilatère plan dont les quatre côtés sont de
même longueur, et dont les sommets sont deux à deux distincts.
Pour ces trois exercices, le plan est muni d’un repère orthonormé direct O,~ı, ~ .
1. Dessiner un quadrilatère dont les quatre côtés sont de même longueur mais qui
n’est pas un losange.
Indication : Relire attentivement la définition d’un losange donnée par l’énoncé !
Vu la définition, un tel quadrilatère aura certains sommets égaux. Par exemple :
B
1
A=C
O
0
1
Il faudra avoir à l’esprit ce genre de cas particuliers dans la suite du problème !
Un quadrilatère dont les diagonales se coupent en
leur milieu et à angle droit est un losange
Pour simplifier nous étudierons un quadrilatère dont un des sommets est l’origine.
Soient donc A, B,et C trois points. Nous supposons que O, A, B, C sont deux à deux
distincts et que les diagonales du quadrilatère OABC sont orthogonales et se coupent
en leur milieu. Le but est de démontrer que OABC est un losange.
On notera a, b, c les affixes respectives de A, B, C.
Remarque : Si les points n’étaient pas deux à deux distincts, les diagonales pourraient
tout simplement ne pas exister, et cet exercice n’aurait plus de sens !
1. Faire une figure.
Comme il s’agit d’un problème de début d’année, on vous demande explicitement
de faire une figure, mais en général n’attendez pas qu’on vous le demande pour en
faire à chaque fois que possible ! Au brouillon, elle est indispensable pour guider
votre réflexion, et au propre, une bonne figure mettra le correcteur en de bonnes
dispositions et pourra même vous rapporter quelque point, même si vous n’avez pas
su trouver le raisonnement formel.
2
Un conseil pour faire une figure : il faut qu’elle soit la plus générale possible : pas
de carré, ne mettez pas de point sur l’axe des abscisses ou des ordonnées...
2
B
C
k
/
1
k
/
A
O 0
1
2
3
2. Quelle est l’affixe du milieu de [OB] ? Et de [AC] ? Ainsi, par hypothèse, ces
deux nombres sont égaux.
L’affixe du milieu est tout simplement la moyenne des affixes.
b+0
a+c
, celle de [AC] est
. Ainsi l’hypothèse selon
2
2
b
a+c
laquelle les diagonales se coupent en leur milieu donne =
, d’où :
2
2
L’affixe du milieu de [OB] est
b = a + c.
(1)
−−→ −→
3. Traduire le fait que OB ⊥ AC.
−−→
−→
L’affixe de OB est b, celle de AC est c − a. On sait alors d’après le cours que ces deux
vecteurs sont orthogonaux si et seulement si :
b · (c − a) + b · (c − a) = 0.
Commentaire : Si vous aviez oublié cette formule, retrouvez-la à l’aide du produit
scalaire :
−−→ −→
−−→ −→
OB ⊥ AC ⇔ OB· AC = 0
⇔
Re (b − 0)(c − a) = 0
⇔
b(c − a) ∈ iR
⇔
⇔
b(c − a) = −b(c − a)
b(c − a) + b(c − a) = 0.
4. En déduire que bc + bc = ba + ba.
Il suffit de développer la formule précédente ! Manifestement, cette question n’est là
que pour donner la formule à ceux qui n’ont pas réussi la question précédente...
5. Montrer que OA = OC.
En combinant les égalités b = a + c et bc + bc = ba + ba on obtient :
donc
donc
donc
(a + c)c + (a + c)c = (a + c)a + (a + c)a
ac + cc + ac + cc = aa + ca + aa + ca
2|a|2 = 2|c|2
|a| = |c|.
car |a| et |c| sont positifs
Comme a est l’affixe de A, et c celle de C, on a bien prouvé que OA = OC.
3
Commentaire : Faisons un petit rappel sur les carrés, qui posent toujours problème
en début d’année. En règle générale, pour tout (x, y) ∈ C2 on a l’équivalence :
x2 = y 2
⇔
(x = y ou x = −y) .
Cependant, dans le cas où on sait à l’avance que x et y sont réels et de même signe,
on obtient :
x2 = y 2 ⇔ x = y.
C’est précisément le cas ici : |a| et |c| sont deux nombres réels et de même signe (positif
en l’occurrence).
6. Achever de montrer que OABC est un losange.
Il reste à montrer que AB = OA et BC = OA.
−→
L’affixe de AB est b − a, donc, en utilisant l’égalité b = a + c :
AB = |b − a| = |a + c − a| = |c| = |a| = OA.
De même :
BC = |c − b| = | − a| = |a| = OA.
Au final, on a bien prouvé que OA = AB = BC = CO, donc le quadrilatère OABC
est un losange.
Les diagonales d’un losange se coupent à angle droit
et en leur milieu
Le but de cette partie est de démontrer que les diagonales d’un losange se coupent
à angle droit et en leur milieu.
Nous prendrons encore un losange dont un des sommets est l’origine du repère.
Nous fixons donc A, B, et C trois points tels que OABC est un losange. Pour simplifier
encore, nous supposons que la longueur des côtés de OABC est 1.
Nous noterons comme dans la partie précédente a, b, et c les affixes respectives des
points A, B, et C.
1
Les diagonales sont orthogonales
1. Que valent |a| et |c| ?
On a |a| = |a − 0| = OA = 1 et |c| = OC = 1.
2. À partir des hypothèses AB = 1 et BC = 1, démontrer :
|b|2 = ab + ab = bc + bc.
L’hypothèse AB = 1 donne |b − a| = 1, d’où |b − a|2 = 1 donc (b − a) · (b − a) = 1. En
développant : bb − ba − ab + aa = 1. Mais comme aa = |a|2 = 1, il reste :
|b|2 − ba − ab = 0.
On obtient de même en partant de BC = 1 que |b|2 = bc + bc.
4
3. Montrer que les diagonales du losange sont orthogonales.
Comme rappelé partie , les diagonales sont perpendiculaires si et seulement si b · (c −
a)+b·(c − a) = 0. Il reste à voir si cela est vrai... Le plus simple quand on ne sait pas
dans quelle direction partir est d’utiliser un raisonnement par équivalence : essayons
de prouver que l’égalité ci-dessus équivaut à une égalité plus simple (et vraie tant
qu’à faire !)
On utilise un raisonnement par équivalence.
−−→ −→
OB ⊥ AC
⇔
⇔
⇔
⇔
b · (c − a) + b · (c − a) = 0
bc − ba + bc − ba = 0
|b|2 − |b|2 = 0
0 = 0.
(question 2)
−−→
−→
Ainsi, l’assertion « OB ⊥ AC » équivaut à l’assertion « 0 = 0 ». Or, cette dernière
−−→ −→
assertion est vraie. Donc l’assertion « OB ⊥ AC » est vraie également.
Ainsi les diagonales de OABC sont orthogonales.
2
Les diagonales se coupent en leur milieu
Dans cette partie, nous admettons que les droites (OB) et (AC) se coupent en
un unique point, que nous notons I.
1. Démontrer que I est le milieu de [OB] et de [AC]. On pourra utiliser le théorème
de Pythagore.
Le triangle OIA est rectangle en
√ I d’après la partie précédente. Le théorème de Pythagore prouve alors que IA = OI 2 + OA2 .
De la même manière en utilisant
le théorème de Pythagore dans le triangle rectangle
√
OIC, on obtient que IC = OI 2 + OC 2 .
Mais OA2 = OC 2 = 1 puisque OABC est un losange de longueur de côtés 1. D’où
IA = IC : I est au milieu de [AC].
On prouve de la même manière que I est le milieu de [OB].
La partie suivante propose de prouver que OABC est un parallélogramme, et
d’en déduire que ses diagonales se coupent en leur milieu d’une manière purement
algébrique, sans admettre le fait que les droites (OB) et (AC) se coupent en un unique
point.
3
*** Un losange est un parallélogramme
Nous allons maintenant prouver que OABC est un parallélogramme. On pose :
−→
• α un argument de l’affixe de OA ;
−−→
• γ un argument de l’affixe de OC ;
−−→
• θ un argument de l’affixe de AB ;
−−→
• ϕ un argument de l’affixe de CB.
5
Cette partie est plus difficile. On utilisera, pour simplifier les calculs, la notation
modulo : étant donnés (a, b, m) ∈ R3 , on notera « a ≡ b [m] » lorsque
∃k ∈ Z tq a = b + km.
1. Division par deux dans un modulo : Soit (a, b, m) ∈ R3 . Vérifier :
a ≡ b [m]
⇔
a ≡ b [2m]
ou
a ≡ b + m [2m] .
• Sens « ⇒ » : Supposons a ≡ b [m]. Il existe alors par définition k ∈ Z tel que
a = b + mk. Fixons un tel k. On considère alors deux cas selon la parité de k :
Si k est pair, il existe ` ∈ Z tel que k = 2`, alors a = b+2`m et donc a ≡ b [2m].
Si k est impair, il existe ` ∈ Z tel que k = 2` + 1, alors a = b + 2`m + m et
donc a ≡ b + m [2m].
• Sens « ⇐ » : Supposons a ≡ b [2m] ou a ≡ m+b [2m]. Dans le premier cas il existe
k ∈ Z tel que a = b + 2mk, dans le second il existe k ∈ Z tel que a = b + m + 2mk.
Dans les deux cas, il existe ` ∈ Z tel que a = b + `m : prendre ` = 2k dans le
premier cas, et ` = 2k + 1 dans le second. Ainsi, dans tous les cas a ≡ b [m].
−→ −−→ −−→
−−→
2. Quelles sont les affixes des quatre vecteurs OA, OC, AB et CB ?
Ces quatre vecteurs sont de norme 1 car ce sont les côtés de notre parallélogramme.
Donc les quatre affixes cherchées ont pour module 1. De plus, par définition, α, γ, θ,
−→ −
−
→ −→
et ϕ sont des arguments de ces quatre affixes. Finalement, les affixes de OA, OC, AB
−−→
iα
iγ
iθ
iϕ
et CB sont, dans l’ordre e , e , e , et e .
3. En écrivant l’affixe de B de deux manières différentes, montrer :
ϕ+θ
α+γ
α−γ
ϕ−θ
= ei 2 sin
.
ei 2 sin
2
2
−→ −→
−
−
→ −−→
D’une part, B = O + OA + AB et d’autre part B = O + OC + CB. Au niveau des
affixes, nous obtenons :
0 + eiα + eiθ = 0 + eiγ + eiϕ .
Vu l’égalité à prouver, on rassemble α et γ d’un côté, et θ et ϕ de l’autre.
Donc :
eiα − eiγ = eiϕ − eiθ .
Comme souvent, on factorise par l’angle moitié. Quoiqu’en réalité, il faudrait plutôt
α+γ
ϕ+θ
parler de « l’angle moyen ». Ici, nous factorisons par ei 2 à gauche, et ei 2 à
droite.
Puis :




α−γ
γ−α
ϕ+θ
ϕ−θ
θ−ϕ
α+γ
i
i
i
i
i
i
e 2 · e 2 − e 2  = e 2 · e 2 − e 2 
donc
donc
i
e
α+γ
ϕ+θ
i
α−γ
ϕ−θ
2 · 2i sin
= e 2 · 2i sin
2
2
(formules d’Euler)
α+γ
ϕ+θ
i
i
α−γ
ϕ−θ
e 2 · sin
= e 2 · sin
.
2
2
(On divise par 2i, qui est non nul.)
6
4. En déduire que :
α − γ ≡ ϕ − θ [2π]
ou
α − γ ≡ θ − ϕ [2π].
On arrive à la partie subtile du raisonnement : les écritures obtenues à la questionprécédente
ne sontdes formes
géométriques de complexes que dans le cas où
α−γ
ϕ−θ
sin
> 0 et sin
> 0. Dans ce cas, ces deux sinus sont les modules
2
2
du terme de gauche et de droite de l’égalité, et sont donc égaux eux-mêmes. De plus
α+γ
ϕ+θ
les nombres
et
sont dans ce cas des arguments des deux membres de
2
2
l’égalité, et sont donc égaux à un multiple de 2π près.
En revanche,
si l’un
de ces
deux sinus est négatif et pas l’autre, alors
α−γ
ϕ−θ
α+γ
ϕ+θ
sin
= − sin
, et on a ∃k ∈ Z tq
=
+ π + 2kπ.
2
2
2
2
Ayez en tête que si un nombre complexe z a pour écriture géométrique z = ρeiθ ,
alors l’écriture z = −ρei(θ+π) ressemble à une écriture géométrique, mais −ρ n’est
pas positif, et donc θ + π n’est pas un argument de z.
De toute façon, ici nous allons juste prendre le module, et tout viendra naturellement.
En prenant le module dans la formule obtenue ci-dessus, il vient :
α−γ ϕ−θ sin
= sin
.
2
2
On rappelle que deux valeurs absolues sont égales si et seulement si les nombres sont
égaux ou opposés.
Donc :
sin
α−γ
2
= sin
ϕ−θ
2
ou
sin
α−γ
2
= − sin
ϕ−θ
2
.
Il y a deux possibilités pour que deux sinus soient égaux. Comme on avait déjà deux
possibilités, on va en avoir quatre au total !
Donc :
ϕ−θ
α−γ
ϕ−θ
α−γ
≡
[2π]
ou
≡π−
[2π]
2
2
2
2
α−γ
ϕ−θ
α−γ
ϕ−θ
ou
≡−
[2π]
ou
≡π+
[2π].
2
2
2
2
En multipliant par 2 :
ou
α − γ ≡ ϕ − θ [4π]
ou
α − γ ≡ 2π − ϕ + θ [4π]
α − γ ≡ −ϕ + θ [4π]
ou
α − γ ≡ 2π + ϕ − θ [4π].
Vous n’avez pas oublié de multiplier aussi le [2π] par deux, n’est-ce pas ?
On peut alors utiliser la question 1 (pour m = 2π). Ces quatre possibilités modulo 4π
reviennent à deux possibilités modulo 2π, et on obtient :
α − γ ≡ ϕ − θ [2π]
ou
α − γ ≡ θ − ϕ [2π].
7
5. Montrer également que :
α + γ ≡ ϕ + θ [2π].
Sachant que sin
α−γ
2
= sin
ϕ−θ
2
l’égalité de la question 3 par sin
ou sin
α−γ
2
α−γ
2
= − sin
ϕ−θ
2
, on veut diviser
. Attention : ne pas oublier de vérifier si ce
nombre est non nul !
Supposons que sin
α−γ
2
= 0.
−→
−
−
→
α−γ
Alors
≡ 0 [π] donc α = γ [2π], donc eiα = eiγ , puis OA = OC, et
2
finalement A = C.
Or, nous avons supposé que les quatre points O, A, B, C sont deux à deux distincts : c’est une contradiction.
L’hypothèse sin
α−γ
2
= 0 est donc absurde, ce qui signifie que sin
Nous pouvons donc diviser l’égalité de la question 3 par sin
nombre est égal à sin
ϕ−θ
2
ei
donc
donc
donc
ou à − sin
α+γ
2
α+γ
i 2
= ei
ϕ+θ
2
ϕ+θ
i 2
e
=e
ϕ+θ
α+γ
≡
[2π]
2
2
α + γ ≡ ϕ + θ [4π]
ϕ−θ
2
α−γ
2
α−γ
2
6= 0.
, et sachant que ce
, on obtient :
ou
ou
ou
ou
ei
α+γ
2
= − ei
α+γ
i 2
ϕ+θ
2
ϕ+θ
e
= ei(π+ 2 )
α+γ
ϕ+θ
≡π+
[2π]
2
2
α + γ ≡ 2π + ϕ + θ [4π].
Alors, d’après la question 1, α + γ ≡ ϕ + θ [2π].
6. Montrer que les quatre situations suivantes sont impossibles :
(a) α ≡ π + θ [2π] ;
Supposons α ≡ π +
θ [2π].
alors au niveau
des
exponentielles
eiα = −eiθ ,
au
niveau
des
vecteurs
−→
−→
OA = −AB.
Alors B
=
−→ −→
O+OA+AB =
−→ −→
O+OA−OA =
O. Ainsi O et
B sont confondus
:
cela
contredit
le fait que
OABC est un
losange
(on
rappelle
que
par définition
les
quatre
sommets
d’un losange
doivent
être
deux à deux
distincts).
(b) γ ≡ π + ϕ [2π] ;
Sur le même principe,
si γ ≡ π + ϕ [2π] on
aurait encore O = B,
ce qui est absurde.
(
(c)
α ≡ θ [2π]
γ ≡ ϕ [2π]
;
Supposons
(
α ≡ θ [2π]
γ ≡ ϕ [2π]
.
8
En
revenant
aux vecteurs,
cela
signifie
−→
−→
que OA = AB
−
−
→
−−→
et OC = CB.
En
mettant le tout
dans
l’égalité
initiale
−→
−→
OA + AB =
−
−
→
−−→
OC + CB,
nous obtenons
−
−
→
−→
2OC = 2OA,
d’où A = C.
Encore
une
fois,
deux
sommets
du
losange
sont
égaux : contradiction.
(
(d)
Si
α = π + ϕ [2π]
θ = π + γ [2π]
(
.
α = π + ϕ [2π]
θ = π + γ [2π]
:
on a cette fois
−→
−−→
OA = −CB et
−
−
→
−→
OC = −AB.
L’égalité
−→
−→
OA + AB =
−
−
→
−−→
OC + CB
devient
−→
−
−
→
OA − OC =
−
−
→
−→
OC − OA
d’où
encore
−→
−
−
→
OA = OC,
contradiction.
Indication : Revenir à l’interprétation géométrique de ces nombres. La contradiction
recherchée sera que les points O, A, B, C ne sont pas deux à deux distincts. Faire des
dessins !
−→ −−→ −−→ −−→
7. Finalement, démontrer que OA = CB et OC = AB, autrement dit que OABC
est un parallélogramme.
Question finale de la partie difficile du devoir ! Il s’agit de rassembler tous les morceaux vus précédemment, et de ne pas se perdre dans les différents cas et sous-cas...
En combinant les résultats des questions 5 et 4 on obtient le système :
(
α − γ ≡ ϕ − θ [2π]
α + γ ≡ ϕ + θ [2π]
(
(
ou
α − γ ≡ θ − ϕ [2π]
α + γ ≡ ϕ + θ [2π]
(
2α ≡ 2ϕ [2π]
2α ≡ 2θ [2π]
ou
.
2γ ≡ 2θ [2π]
2γ ≡ 2ϕ [2π]
(en additionnant et soustrayant les deux lignes)
donc
C’est clairement le système de gauche qu’on aimerait savoir vérifié. Essayons donc
de prouver que le système de droite est impossible.
(
Supposons que
2α ≡ 2θ [2π]
2γ ≡ 2ϕ [2π]
.
9
La première équation devient, en vertu de la question 1, α ≡ θ [2π] ou
α ≡ π + θ [2π]. La seconde éventualité est impossible par la question 6, il
reste donc uniquement α ≡ θ [2π].
De même, la seconde ligne du système donne γ ≡ ϕ [2π] ou γ ≡ πϕ [2π], mais
la seconde relation est impossible,
la bonne est donc γ ≡ ϕ [2π].
(
Nous avons ainsi obtenu
α ≡ θ [2π]
γ ≡ ϕ [2π]
, mais ceci est encore impossible tou-
jours par la question 6.
(
2α ≡ 2θ [2π]
2γ ≡ 2ϕ [2π]
En conclusion, le système
est impossible. C’est donc l’autre système
qui est vérifié, à savoir :
(
2α ≡ 2ϕ [2π]
2γ ≡ 2θ [2π]
,
qui devient via la question 1 :
(
α ≡ ϕ [2π] ou α ≡ π + ϕ [2π]
γ ≡ θ [2π] ou γ ≡ π + θ [2π]
.
(2)
Pour la conclusion finale, procédons encore une fois par l’absurde.
−→
−−→
Supposons que OABC n’est pas un parallélogramme, donc que OA 6= CB ou que
−
−
→ −→
OC 6= AB.
−→ −−→
• Premier cas : supposons OA 6= CB. Ainsi, α 6≡ ϕ [2π]. Alors, vu 2,
on obtient α ≡ π + ϕ [2π].
Il est alors impossible 1 que γ ≡ π + θ [2π] d’après la question 6.
−
−
→ −→
On déduit que γ ≡ θ[2π]. Au niveau des vecteurs, ceci devient OC = AB.
−→ −→ −
−
→ −−→
−→ −→
Mais alors l’égalité OA + AB = OC + CB donne OA = AB.
−→ −→
−→ −→
En supposant OA 6= AB on déduit que OA = AB, c’est absurde !
−
−
→
−→
• Second cas : supposons OC 6= AB. C’est le même principe : on
−→
−→
obtient γ ≡ π + γ [2π], puis α ≡ ϕ [2π] donc OA = AB et OABC est
quand même un parallélogramme !
−→
−−→
−
−
→
−→
En conclusion, il est impossible que OA 6= CB ou OC 6= AB, ce qui signifie que
−→ −−→
−
−
→ −→
OA = CB et OC = AB et OABC est un parallélogramme !
4
Les diagonales se coupent en leur milieu
1. Exprimer b en fonction de a et c. On pourra utiliser le résultat de 3.
−→ −−→
−→
−−→
Comme OA = CB, l’affixe de OA est égale à l’affixe de CB ce qui donne :
a = b − c.
D’où immédiatement :
b = a + c.
1. On utilise donc un raisonnement par l’absurde à l’intérieur d’un raisonnement par l’absurde !
10
2. Montrer que le milieu de [OB] est égal au milieu de [AC].
Indication : Calculer l’affixe du milieu de [OB], du milieu de [AC] et vérifier que ce
sont les mêmes.
0+b
b
c+a
L’affixe du milieu de [OB] est
c.-à-d. , celle du milieu de [AC] est
.
2
2
2
Comme b = a + c par la question 1, ces deux affixes sont les mêmes, ce qui signifie
que les deux points sont confondus. Ainsi le milieu de [OB] est également le milieu de
[AC].
Commentaire : Pour cette question, on a seulement utilisé la relation b = a + c qui
−→ −−→
venait de ce que OA = CB. Donc la propriété prouvée est vraie pour n’importe quel
parallélogramme, et pas seulement pour les losanges.
On a bien prouvé que les diagonales du losange OABC se coupent à angle droit
et en leur milieu.
Une équation dans le cercle trigonométrique
Ici, le but est de déterminer les nombres complexes a, b, c de module 1 tels que
a + b + c = 1 en utilisant quelques résultats des parties précédentes.
1. Donner un exemple de triplet (a, b, c) ∈ U3 vérifiant a + b + c = 1. Dessiner les
points du plan correspondant.
Par exemple, a = i, b = −i, c = 1. Plus généralement, il suffit de prendre 1 puis deux
nombres de module 1 opposés.
Remarque : On obtient un triangle rectangle inscrit dans un cercle.
1
a
c
−1
0
1
b
−1
Dans la suite, on fixe a, b, c trois nombres complexes de module 1 vérifiant
−−→
−−→
a + b + c = 1. On définit les points M , N et P tels que OM = a, M N = b, et
−−→
N P = c.
2. On suppose que les points O, M, N, P sont deux à deux distincts. Démontrer
que OM N P est un losange. En déduire la valeur de b.
−−→
Déjà, OM = ||OM || = |a| = 1. De même, M N = 1 = N P .
−
−
→
−
−
→ −−→ −−→ −−→
Il reste le quatrième côté : P O = ||P O||. Or, P O = OM + M N + N O. Donc l’affixe
−
−
→
de P O vaut a + b + c, qui vaut donc 1. Et pour la longueur : P O = |1| = 1.
En conclusion, les quatre côtés de notre quadrilatère OM N P ont la même longueur,
comme de plus les quatre points sont deux à deux distincts, c’est un losange.
−−→
−
−
→
On a vu qu’un losange est un parallélogramme. Ainsi, M N = P O. Nous venons de
−
−
→
−−→
voir que l’affixe de P O est 1. Donc l’affixe de M N est 1 aussi, c.-à-d. b = 1.
3. Démontrer que dans tous les cas, un des trois nombres a, b, ou c vaut 1. Comment
sont alors les deux autres nombres ? Représenter le tout dans le plan.
11
Indication : Le cas où les points O, M, N, P est évident grâce à la question précédente.
Il vous faut donc étudier les cas où deux de ces points seraient égaux. Attention :
certains de ces points ne peuvent pas être égaux.
Le cas où les 4 points sont deux à deux distincts est réglé : dans ce cas c’est b qui
vaut 1.
Il nous reste le cas où deux points seraient égaux. Notons tout de suite que deux
points consécutifs du quadrilatère ne peuvent être égaux car leur distance est 1 (par
la question 2). Donc les points pouvant être égaux sont (O et N ), ou (M et P ) 2 .
−
−
→ −−→ −−→
• Cas où O = N : Comme OP = OM + M N , l’affixe de P est a + b. Nous obtenons
alors que a + b = 0.
Alors l’hypothèse initiale a + b + c = 1 donne c = 1.
−−→ −−→ −−→
• Cas où M = P : Ainsi, ~0 = M P = M N + N P . Au niveau des affixes : b + c = 0.
D’où nous déduisons a = 1.
Ainsi, dans tous les cas, un des trois nombres vaut 1.
Les deux autres nombres sont alors opposés.
2. Ces parenthèses sont mathématiques et non littéraires.