l`organigramme des quadrilatère particuliers.

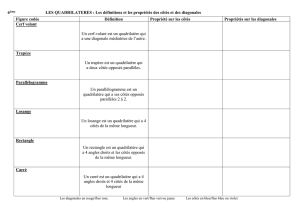
Quadrilatères particuliers :
c’est un
parallélogramme
DONNEES
Si un
parallélogramme a 1
angle droit, alors
Si un
parallélogramme a
ses diagonales de
même longueur, alors
Si un
parallélogramme a 2
côtés consécutifs de
même longueur, alors
Si un parallélogramme
a ses diagonales
perpendiculaires, alors
c’est un
rectangle
c’est un
losange
alors c’est un
CARRE
Définition : Un quadrilatère a 4 côtés de
même longueur ….
Si un quadrilatère non croisé a 2 côtés
opposés parallèles et de même longueur,
alors
Si un quadrilatère a ses diagonales
qui se coupent en leur milieu, alors
Un quadrilatère ayant ses opposés
parallèles 2 à 2 ….
Si un quadrilatère non croisé a ses côtés
opposés 2 à 2 de même longueur, alors
Un quadrilatère ayant 3 angles droits….
définition
définition
Un carré est un quadrilatère qui a 3 angles
droits et 4 côtés de même longueur.
définition
DONNEES CONCLUSION
CONCLUSION
Si un rectangle a ses
diagonales
perpendiculaires
Si un rectangle a deux
côtés consécutifs
de même longueur
Si un losange a un
angle droit
Si un losange a
ses diagonales
de même longueur
DONNEES CONCLUSION
Si un quadrilatère a ses angles opposés de
même mesure 2 à 2 ( les angles consécutifs
sont supplémentaires), alors