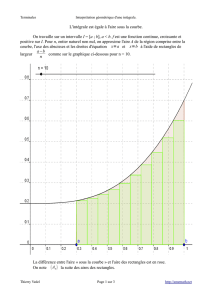
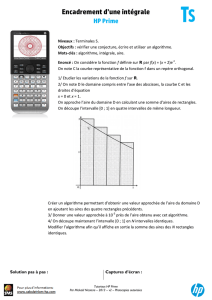
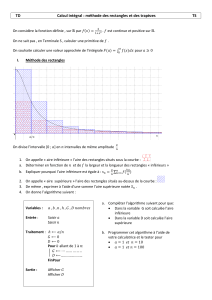
TD 12 : Intégration numérique Méthode des rectangles Méthode des

n
f
f
Zb
a
f(t)dt 'b−a
n
k=n−1
X
k=0
fa+kb−a
n
ai=a+kb−a
n
∀x∈[ai;ai+1]|f(x)−f(ai)|6M1|x−ai|M1f0
[a;b]
Zai+1
ai
f(t)dt f(ai)b−a
n
f[a;b]
a= 0 b= 1
M1610 n
0.01 10−9
f(ai)
(ai, f(ai)) (ai+1, f(ai+1))
x
[ai, ai+1]f(x)
(ai+1 −x)(x−ai)M2
2M2|f00|[a;b]

a= 0 b= 1 M26100
n0.01
10−9
f
a
b
n