vecteurs_logique nov. 2009

Devoir de mathématiques à rendre pour le 30/11/2009
Exercice 1 : Quantificateurs
Dans le langage usuel, quand on dit « Tous les Français sont européens », on veut exprimer le fait que tout
Français, quel qu’il soit, est un Européen.
Quand on dit « un Français est daltonien », on veut exprimer le fait qu’il existe au moins un Français qui est
daltonien.
En mathématiques, on utilise souvent les expressions « quel que soit » ou « il existe », appelées
quantificateurs. Ces expressions sont parfois implicites.
Par exemple :
_Quels que soient les réels a et b, (a + b)2 = a2 + 2ab + b2.
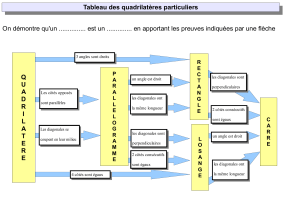
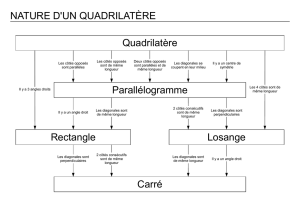
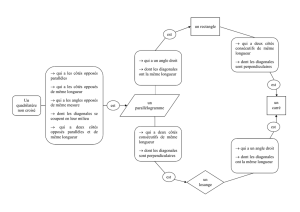
_« Les diagonales d’un losange sont perpendiculaires » signifie que tous les losanges ont leurs diagonales
perpendiculaires.
_Le carré d’un réel est positif : cette proposition est vraie quel que soit le nombre réel.
_Il existe un nombre entier pair supérieur à 1000 000.
_Il existe deux réels x vérifiant l’égalité x(x – 3) = 0.
_Pour tout réel x, on a x(x – 3) = x2 – 3x.
_Quel que soit le triangle ABC rectangle en A, BC2 = AB2 + AC2.
Dans cet exercice, on appelle DIAGONALE d’un polygone régulier tout segment de droite joignant deux sommets
non consécutifs du polygone. Ainsi, un triangle équilatéral ne possède aucune diagonale et un carré en possède
deux.
1. Dans le tableau suivant, qui est à compléter et à rendre avec la copie, tracer en couleur toutes diagonales des
polygones réguliers à 5 et 6 côtés, puis indiquer leur nombre dans la ligne suivante.
Dans la suite de l’exercice, on admet que le nombre d de diagonales d’un polygone régulier à n côtés (n étant un
n(n – 3)
entier naturel supérieur ou égal à 3) est donné par la formule : d =
.
2
2. Dans cette question, on cherche à déterminer dans quels polygones réguliers le nombre d de diagonales est un
multiple entier du nombre n de côtés.
a) Exploiter ce qui a été fait dans les questions précédentes pour dire si chacune des propositions suivantes est
VRAIE ou FAUSSE. Chaque réponse doit être justifiée.
Proposition no 1 : Il existe au moins un polygone régulier pour lequel le nombre de diagonales est le double
du nombre de côtés.
Proposition no 2 : Quel que soit un polygone régulier, le nombre des diagonales de ce polygone est le double
du nombre de ses côtés.
o
Proposition n 3 : Quel que soit un polygone régulier, le nombre des diagonales de ce polygone est un
multiple entier du nombre de ses côtés.
b) On considère l’algorithme suivant :
Variables :
k, n deux entiers ;
d un réel ;
Entrée :
saisir k ;
Initialisation : donner à n la valeur initiale de 3 ;
donner à d la valeur initiale de 0 ;
Traitement : Tant que d < k × n faire
affecter à n la valeur n + 1;
n(n – 3)
donner à d la valeur
;
2
FinTantque ;
Sortie :
Afficher n et d ;
Faire fonctionner l’algorithme pour k = 3.
k
n
d
initialisation
étape 1
étape 2
Interpréter le résultat obtenu en termes de nombres de côtés et de
diagonales d’un polygone régulier.
c) Démontrer que, pour un entier naturel non nul k donné, d = k × n si et seulement si n = 2k + 3.
En déduire les polygones réguliers dans lesquels le nombre d de diagonales est un multiple entier du nombre
de côtés.
Exercice 2 :
Soient ABC un triangle non équilatéral,
O le centre de son cercle circonscrit et G son centre de gravité.
Soient A’, B’ et C’ les milieux
respectifs
des→
segments [BC], [AC] et [AB].
→
→
→
Soit H le point défini par OH = OA + OB + OC.
→
→
1.a) Que vaut A’B + A’C ?
b) En utilisant la→
relation
de Chasles
et le point A’,
→
→
justifier que OB + OC = 2 OA’.
c) En utilisant→
la relation
de→
Chasles
et la →
question→
1.a),
→
→
déduire de OH = OA + OB + OC que AH = 2 OA’.
d) En déduire que les droites (AH) et (BC) sont perpendiculaires.
2. Faire un raisonnement analogue pour prouver que (BH) et (AC) sont perpendiculaires.
3. Que représente →
le point H →
pour le triangle ABC ?
4.a) Montrer que GA = – 2 GA’.
→
→
→
→
→
b) En partant de l’égalité GA = – 2 GA’, montrer →
que 3 OG
= OA + 2 OA’.
→
c) En déduire, en utilisant la question 1.b), que 3 OG = OH.
5. En déduire que les points O, G et H sont alignés.
On vient de montrer que l’orthocentre, le centre de gravité et le centre du cercle circonscrit d’un triangle était
toujours alignés. Cette droite s’appelle droite d’Euler du nom du mathématicien suisse Leonhard Euler
(1707-1783) à qui l’on doit la découverte et la démonstration de ce résultat.