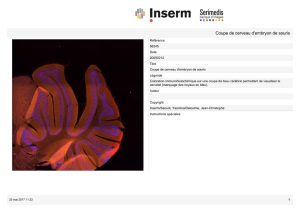
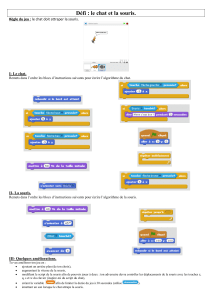
Modèle mathématique.

Terminale S1- Spécialité mathématiques 27/05/2013
Devoir surveillé N°7 : 50 minutes
Exercice 1 : Dynamique des populations 12 points
Dans une population de souris femelles, une souris donne naissance à une femelle pendant sa
première année de vie et à huit femelles durant sa deuxième année. La probabilité qu'une souris
femelle survive une deuxième année est de 25 % et il n'y a aucune chance qu'elle survive au delà
de la deuxième année. On distingue donc deux catégories de souris : les jeunes, âgées de moins
d'un an et les adultes dont l'âge est compris entre 1 et 2 ans.
On note pour
jn
le nombre de souris jeunes,
an
le nombre de souris adultes,
et
tn
le nombre total de souris femelles après
n
années.
NB : On ne tient pas compte dans cet exercice des souris mâles, mais il y en a probablement... il
paraît que c'est plus facile pour la reproduction.
1 – Montrer que les hypothèse de l'énoncé peuvent se traduire par le
système
{
jn+1=jn+8 an
an+1=0,25 jn
, noté (S) dans la suite de l'énoncé.
On étudie dans la suite une population dont l'effectif initial est de vingt
jeunes femelles et aucune souris adulte.
2 – On considère la matrice
L=
(
1 8
0,25 0
)
, baptisée matrice de Leslie, nom du
mathématicien qui a introduit cette modélisation en 1945, et on représente la
population des souris femelles après n années sous la forme :
Vn=
(
jn
an
)
.
a) Donner une écriture matricielle du système (S).
b) En déduire une expression de
Vn
en fonction de
n
,
V0
et
L
.
3 – Calcul de
Ln
.
a) Déterminer tous les réels
x
tels que la matrice
L−xI 2
ne soit pas
inversible (on notera et ces nombres, étant    le plus grand des deux).
b) Déterminer deux matrices colonnes non proportionnelles
V
et
W
telles que
LV = V
et
LW = W
.
c) En déduire une matrice
P
et une matrice
D
telles que
P−1LP=D
.
d) Démontrer que pour tout entier naturel non nul,
Ln=P−1DnP−1
.
e) Calculer
Dn
, puis démontrer que
Vn=1
12
(
8×2n+4×(−1)n32×2n−32×(−1)n
2n−(−1)n4×2n+8×(−1)n
)
×
(
20
0
)
4 – Evolution à long terme de la population : (Bonus, 2 points)
a) Exprimer en fonction de
n
le nombre total
tn
de souris.
b) Déterminer
lim
n→+∞
tn+1
tn
et interpréter ce résultat quant-à la nature de
l'évolution de la population de ces souris selon ce modèle.
Exercice 2 : Un tout petit site web... 8 points
Un surfeur se déplace de manière aléatoire sur un tout petit site composé de trois pages
désignées par les lettres A, B et C. La page d'accueil A renvoie vers les pages B et C, chacune
des pages B et C permet de revenir à la page d'accueil. Il n'existe pas de lien direct la page B et
la page C. Avec une probabilité de 0,7 le surfeur choisit au hasard l'un des liens proposés par la
page sur laquelle il se trouve, sinon, il est envoyé de manière aléatoire et équiprobable sur
l'une des trois pages (donc éventuellement sur celle où il est déjà).
1 – Le surfeur est à l'étape 0 sur la page d'accueil de ce superbe site.
Réprésenter par un arbre pondéré le passage de l'étape n à l'étape n+1 (on
pourra distinguer les déplacements avec saut et sans saut).
2 – On note
Xn=(anbncn)
la matrice ligne donnant les probabilités que
le surfeur soit respectivement sur la page A, B et C après n clics.
Donner
X0
, puis déterminer
X1
et
X2
3 – a) Déterminer une matrice carrée
M
et une matrice
N
ligne telles
que l'on puisse écrire
Xn+1=Xn×M+N
.
b) En déduire
X3
puis
X4
à l'aide d'une calculatrice.
4 – Démontrer que pour tout entier naturel
n
,
bn=cn
.
En déduire une relation entre
an+1
et
an
.
5 – Bonus (1 point)
Etudier la convergence de la suite
(an)
et déterminer sa limite éventuelle.
Interpréter ce résultat.