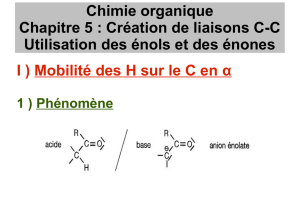
Théorie de l`indice et géométrie basique d`un feuilletage riemannien

AVERTISSEMENT
Ce document est le fruit d'un long travail approuvé par le jury de
soutenance et mis à disposition de l'ensemble de la
communauté universitaire élargie.
Il est soumis à la propriété intellectuelle de l'auteur. Ceci
implique une obligation de citation et de référencement lors de
l’utilisation de ce document.
D'autre part, toute contrefaçon, plagiat, reproduction
encourt une poursuite pénale.
illicite
Contact : [email protected]
LIENS
Code de la Propriété Intellectuelle. articles L 122. 4
Code de la Propriété Intellectuelle. articles L 335.2- L 335.10
http://www.cfcopies.com/V2/leg/leg_droi.php
http://www.culture.gouv.fr/culture/infos-pratiques/droits/protection.htm
Université Paul Verlaine, Metz
Thèse
présentée pour obtenir le grade de
Docteur en Mathématiques
par
Alexandre REY ALCANTARA
Théorie de l'indice et géométrie basique
d'un feuilletage riemannien
Soutenue publiquement le 2 novembre 2011, devant le jury
composé de :
Moulay-Tahar Benameur
(PR Metz, Directeur de thèse)
Sylvie Paycha
(PR Clermont-Ferrand, Rapporteur)
Alexander Gorokhovsky
(Associate PR Boulder, Rapporteur)
Jean-Louis Tu
(PR Metz, Examinateur)
Jean Renault
(PR Orléans, Examinateur)
Martin Schlichenmaier
Varghese Mathai
(PR Luxembourg, Examinateur)
(PR Adelaide, Australie, Examinateur)
1
Remerciements
Je voudrais remercier Moulay-Tahar Benameur qui a bien voulu encadrer
ma thèse. Je le remercie pour tout le temps qu'il a bien voulu m'accorder,
pour les opportunités qu'il m'a proposées, et j'en prote pour saluer ses
grandes qualités pédagogiques.
Je voudrais remercier Alexander Gorokhovsky et Sylvie Paycha d'avoir
bien voulu rapporter ma thèse et d'avoir consacrer autant de temps à sa relecture. Je remercie également Jean-Louis Tu, Jean Renault, Varghese Mathai
et Martin Schlichenmaier d'avoir accepté de faire partie de mon jury.
Je voudrais témoigner de ma reconnaissance à Aziz El-Kacimi pour m'avoir
acceuilli à Lille, pour avoir répondu à mes nombreuses questions et m'avoir
délivré de très bons conseils et de précieuses explications tout au long de ce
travail. Je voudrais également remercier Alexander Gorokhovsky, Gaël Meigniez et Gilbert Hector, qui ont bien voulu discuter avec moi et me prodiguer
d'excellents conseils.
Je souhaiterais remercier les membres du LMAM avec qui j'ai travaillé
durant ces quatre dernières années, plus particulièrement l'équipe de Géométrie Non-Commutative et les collègues avec qui j'ai collaboré pour mes
enseignements. Je citerais parmi eux Nicolas Louvet, Philippe Bonneau, Nicolas Prudhon et Dong Ye. Je remercie également Angela Pasquale qui a
toujours accepté de répondre à mes questions avec énormément de gentillesse.
Je voudrais remercier mes collègues doctorants du LMAM pour tous les
bons moments que nous avons passés ensemble et pour la solidarité qui s'est
toujours exprimée entre nous. Je citerais parmi eux Frédéric Albert, Indrava
Roy, El-Kaïoum Moutuou, Stéphane Garnier, Mikaël Chopp et en particulier Jérôme Noël qui m'a oert à de nombreuses reprises sa précieuse aide
et sans qui j'aurais passé des pauses de midi bien plus moroses. Je voudrais
également remercier mes collègues de bureaux Imen Ayadi et Ivan Lassagne
avec qui j'ai partagé d'excellents moments et qui me manqueront.
Je souhaiterais également remercier la formidable secrétaire du LMAM
Isabelle Naviliat.
Je voudrais saluer les doctorants que j'ai rencontré lors de conférences
et avec qui j'ai passé de très bons moments, en particulier Haïja Moustafa,
Maria-Paula Gomez-Aparicio, et Nicolas Hussenot.
Je voudrais proter de cette occasion pour témoignier à Chakib Bennis
de la profonde gratitude que j'ai à son égard pour tout le temps qu'il a bien
2
voulu m'accorder tout au long de mes études, pour les conseils qu'il m'a
prodigué durant ces dix dernières annés et pour tout ce qu'il a fait pour moi.
Je crois qu'il est temps de lui avouer que c'est lui qui a fait naître en moi la
vocation de l'enseignement.
Je tiens à témoignier ma reconnaissance à Dorin Bucur pour les précieux
conseils qu'il m'a délivrés à de très nombreuses reprises, pour le temps qu'il
a bien voulu m'accorder et pour m'avoir incité à entreprendre ce travail et
pour m'avoir toujours prodigué de judicieux conseils.
Je voudrais spécialement remercier Anne Lux pour tout le temps qu'elle
a bien voulu m'accorder, et je sais combien son temps est précieux. Je voudrais la remercier pour les nombreux conseils qu'elle m'a prodigués et pour
l'aide formidable qu'elle m'a apporté durant les six semaines où j'ai eu la
chance de la remplacer au lycée Fabert de Metz.
Je voudrais remercier mes collègues du lycée Fabert qui se sont montrés
particulièrement accueillants et qui m'ont beaucoup soutenus durant le bref
séjour que j'ai eectué auprès d'eux. Je voudrais citer particulièrement JeanDenis Eiden, Sylvie Larose et Christiane Vincent.
Je tiens également à remercier tous mes collègues actuels du lycée Henri
Poincaré de Nancy dont l'aide et le soutien me sont très précieux.
Je voudrais remercier ma famille. Tout d'abord mon beau-père Didier
pour son soutien, ses encouragements, son aide et puis tout simplement parce
que je sais qu'il est très er de moi. Je voudrais remercier mes frères d'avoir
supporté pendant toutes ces années mes cassages de pieds, mes exigences,
ma mauvaise humeur (cette liste n'est pas exhaustive) et puis aussi de ne
pas avoir pris assez de temps pour eux.
Je tiens absolument à proter de cette occasion pour remercier ma mère
pour tout ce qu'elle a fait pour moi. Pour l'éducation qu'elle m'a donnée,
pour s'être occupé avec autant de ferveur de sa famille, pour avoir tout fait
pour que je puisse prendre en mains mon destin. Elle a été à mes côtés durant toutes mes études, m'a toujours encouragé, soutenu, assisté et a tout fait
pour faciliter ma réussite. Je n'aurais jamais eu l'occasion de faire des études
sans elle et je n'aurais certainement pas accompli un aussi beau parcours. Je
sais combien elle est ère de moi et combien elle aurait aimé pouvoir être à
ma place. Je tiens donc à lui témoigner ma plus profonde gratitude.
Je souhaiterais remercier ma tendre compagne Jeanne-Sophie qui m'a
encouragé, soutenu, supporté mes sauts d'humeurs, mes baisses de moral,
mes lamentations, mes maux de tête à répétition, et qui est restée à mes
3
côtés tout au long de ces années. Je lui dois beaucoup.
Je voudrais nir en remerciant mon pays, ma patrie la France. Durant
ces quatre dernières années, l'idée de perpétuer la tradition française des
mathématiques, d'entretenir la réputation des mathématiques françaises m'a
toujours accompagnée. Je ne saurais cacher l'amour que je voue à mon pays,
celui qui a acceuilli mes parents immigrés, qui m'a vu grandir, qui m'a nourri,
soigné et éduqué et qui ne m'a jamais reproché mon nom aux sonorités
étrangères.
4
Table des matières
1 Introduction
7
2 Rappels sur les opérateurs diérentiels
2.1
2.2
12
Opérateurs diérentiels . . . . . . . . . . . . . . . . . . . . . .
12
2.1.1
Opérateurs diérentiels elliptiques
. . . . . . . . . . .
12
2.1.2
L'opérateur de signature . . . . . . . . . . . . . . . . .
16
2.1.3
L'opérateur de Dolbeault
. . . . . . . . . . . . . . . .
17
2.1.4
L'opérateur de Dirac . . . . . . . . . . . . . . . . . . .
19
Actions de groupes compacts
. . . . . . . . . . . . . . . . . .
2.2.1
Cohomologie de de Rham invariante
. . . . . . . . . .
22
2.2.2
Opérateurs diérentiels invariants . . . . . . . . . . . .
24
2.2.3
L'opérateur de signature invariant
. . . . . . . . . . .
26
2.2.4
L'opérateur de Dolbeault invariant . . . . . . . . . . .
28
3 Feuilletages riemanniens
3.1
3.2
22
29
Connexion et courbure . . . . . . . . . . . . . . . . . . . . . .
29
3.1.1
La connexion de Levi-Civita transverse . . . . . . . . .
29
3.1.2
Courbure principale
. . . . . . . . . . . . . . . . . . .
33
Géométrie basique d'un feuilletage riemannien . . . . . . . . .
37
3.2.1
Généralités
. . . . . . . . . . . . . . . . . . . . . . . .
37
3.2.2
Cohomologie basique pour les suspensions . . . . . . .
41
3.2.3
Forme volume transversale et opérateur de Hodge basique . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 Opérateurs diérentiels basiques
44
50
4.1
Opérateurs transversalement elliptiques
. . . . . . . . . . . .
50
4.2
Le Laplacien basique . . . . . . . . . . . . . . . . . . . . . . .
61
4.3
L'opérateur de de Rham basique
. . . . . . . . . . . . . . . .
67
4.4
L'opérateur de signature basique
. . . . . . . . . . . . . . . .
68
4.5
L'opérateur de Dolbeault basique . . . . . . . . . . . . . . . .
73
4.6
L'opérateur de Dirac basique
4.7
Exemples
4.7.1
. . . . . . . . . . . . . . . . . .
75
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
Exemples de calculs de signature basiques . . . . . . .
79
5
4.7.2
Exemples de calculs d'indice de l'opérateur de Dolbeault basique
. . . . . . . . . . . . . . . . . . . . . .
87
5 Invariance par homotopie feuilletée de la signature basique 93
6 L'indice basique en tant qu'indice distributionnel
98
6.1
Existence de l'indice distributionnel . . . . . . . . . . . . . . .
6.2
Le cas des actions libres
98
6.3
Multiplicativité et excision . . . . . . . . . . . . . . . . . . . . 107
6.4
Lien avec l'indice basique et l'indice équivariant . . . . . . . . 114
. . . . . . . . . . . . . . . . . . . . . 104
A Généralités sur les feuilletages et théorie de Molino
117
A.1
Premières dénitions . . . . . . . . . . . . . . . . . . . . . . . 117
A.2
Structures transverses
A.3
Holonomie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
A.4
Théorie de Molino
. . . . . . . . . . . . . . . . . . . . . . 120
. . . . . . . . . . . . . . . . . . . . . . . . 123
B Notion de F -brés
125
C Index
130
6
Chapitre 1
Introduction
La notion de feuilletage a été introduite dans les années 1940 par Erehsmann et Reeb. Elle a été ensuite développée par Haeiger, Novikov, Thurston, ...[Thu74, Nov63, Hae58]. Dans le cas d'un feuilletage riemannien, la
cohomologie des formes diérentielles basiques introduite par B. Reinhart
[Rei59a], qui est alors de dimension nie [EKASH85], a joué un rôle important dans la production d'invariants topologiques pour ces feuilletages. Il est
ainsi possible par exemple de dénir, comme dans le cas d'une variété fermée, la caractéristique d'Euler basique ou encore la signature basique d'un
feuilletage riemannien.
De plus il a été démontré dans [EKA90] que ces invariants sont des indices
de Fredholm d'opérateurs diérentiels
basiques
transversalement elliptiques
sur le feuilletage. A. El Kacimi a plus précisement prouvé que tout opérateur
diérentiel basique transversalement elliptique sur un feuilletage riemannien
possède un indice de Fredholm appelé
indice basique.
La question naturelle qui s'est alors posée est le calcul de tels indices par
des formules topologiques. C'est ce que nous appellerons dans cette thèse le
problème de l'indice basique, il a été posé pour la première fois dans [EKA90].
Le problème de l'indice basique s'est avéré assez dicile et malgré plusieurs tentatives, il est resté ouvert jusqu'en 2010. En 2010 deux travaux
importants ont été réalisés indépendamment par A. Gorokhovsky et J. Lott
[GL10] et par J. Bruning, F. Kamber et K. Richardson [BKR10a, BKR10b]
et ont permis de donner les premières formules d'indice basique. Dans l'article [GL10], une formule topologique est obtenue sous certaines hypothèses
sur le faisceau de Molino, en utilisant une approche classique appuyée en partie sur la formule de l'indice d'Atiyah-Segal-Singer [AS68]. Dans [BKR10a,
BKR10b], aucune hypothèse importante n'est imposée au feuilletage riemannien et la formule obtenue est une somme de contributions associées à la
stratication par les adhérences des feuilles. Ce dernier travail ne fournit pas
de formule topologique aussi explicite que la formule d'Atiyah-Singer.
Le problème de l'indice basique est intimement lié au célèbre problème
7
de l'indice pour les opérateurs transversalement elliptiques pour les actions
de goupes de Lie compacts sur des variétés fermées, tel qu'énoncé par M.
F. Atiyah dans [Ati]. La solution du problème de l'indice basique a donc
des conséquences sur le calcul des multiplicités de certaines représentations
de groupes de Lie compacts dans la
représentation indice
dénie par Atiyah
[Duf].
Même si le problème de l'indice transverse d'Atiyah est toujours ouvert, des réponses partielles ont été apportées par N. Berline et M. Vergne
dans l'article [BV96b] ainsi que dans [BV96a]. Les formules de délocalisation
de Berline-Vergne pourraient donc en principe fournir grâce au théorème
de Molino, des informations importantes sur l'indice basique d'un opérateur
diérentiel basique transversalement elliptique sur un feuilletage riemannien.
Parce que la formule de Berline-Vergne ne permet pas de calculer les multiplicités, une telle approche ne sut pas à calculer l'indice basique par une
formule topologique.
Nous avons choisi dans ce travail une approche uniant les deux probblèmes de l'indice. Plus précisément, le problème de l'indice basique d'El
Kacimi et le problème de l'indice transverse d'Atiyah peuvent être generalisés et uniés en un seul problème introduit et étudié dans cette thèse. Nous
nous intéressons à la situation d'un feuilletage riemannien muni d'une action
G et à l'étude des opérateurs basiques
(G, F)-transversalement elliptiques, c'est-à-dire dont
restreint à la fois aux orbites de G et au feuilletage F
feuilletée d'un groupe de Lie compact
G-invariants
qui sont
le symbole principal
est inversible. Nous démontrons que de tels opérateurs possèdent un
basique distributionnel
qui est une distribution centrale sur
G.
indice
Lorsque le
feuilletage est de dimension maximale (formé d'une seule feuille, la variété
ambiante) on retrouve la notion d'opérateurs
et leur indice selon Atiyah. Lorsque le groupe
G-transversalement elliptiques
G est le groupe trivial G = {e}
on retrouve la notion d'opérateurs basiques transversalement elliptiques par
rapport au feuilletage et leur indice basique selon El Kacimi. Le cas général étudié dans cette thèse peut donc être naïvement compris comme une
interpolation entre ces deux situations géométriques extrêmes. Dans le cas
général, notons que si l'opérateur basique est transversalement elliptique
pour le feuilletage, alors l'indice distributionnel appartient à
R(G).
Comme dans Atiyah nous démontrons que l'indice distributionnel basique
satisfait aux axiomes habituels d'excision et multiplicativité. Nous donnons
aussi la formule obtenue dans le cas des actions libres. Enn l'application
du théorème de Molino nous permet, comme dans le cas sans action décrit
plus haut, de relier l'indice distributionnel basique à un indice distributionnel d'Atiyah classique sur la variété basique du feuilletage et relativement
au produit cartésien de
G
par le groupe orthogonal transverse.
Nous allons maintenant décrire plus en détails les résultats démontrés
dans ce travail. Lors de notre étude des invariants géométriques provenant
8
d'opérateurs basiques, nous étudions la signature basique
σ(M/F).
En éta-
blissant un "lemme de Poincaré basique", nous démontrons le résultat suivant :
Théorème.
34 Soit
f : (M, F) → (N, F 0 )
une équivalence d'homotopie
feuilletée, entre deux feuilletages riemanniens homologiquement orientables,
préservant les orientations. Alors
σ(N/F 0 ) = σ(M/F).
Nous étudions ensuite la situation d'un feuilletage riemannien muni d'une
action d'un groupe de Lie compact
G.
En suivant l'article d'Atiyah [Ati], et
en l'adaptant au cas des feuilletages, nous montrons alors qu'un opérateur
G-invariant
basique transversalement elliptique par rapport à l'action du
groupe et du feuilletage, admet un indice distributionnel basique :
Théorème.
On note
35 On suppose que
χker D
D
(G, F)-transversalement elliptique.
ker D. Alors χker D est bien
]
−
dim
W
H
(G).
est
le caractère de la représentation
déni et vit dans l'espace de Sobolev
G
On note ind−∞,B (D)
butionnel basique.
= χker D − χker D∗
que nous appelons ici indice distri-
Nous étudions ensuite les propriétés de cet indice distributionnel. Nous
commençons par étudier le cas des actions libres : on suppose qu'on a une
G × H tel que H agit
librement sur la variété M . On a donc un bré principal M → M/H . On suppose de plus que M/H est muni d'un feuilletage riemannien F qui se relève
]
sur M en un feuilletage riemannien F et que toutes les actions considérées
sont feuilletées. Un opérateur diérentiel D (G, F)-transversalement ellip]
tique sur M/H se relève alors en un opérateur (G × H, F )-transversalement
]
elliptique D . L'indice de ce dernier se calcule alors à partir de l'indice de D
action lisse d'un groupe de Lie compact de la forme
de la manière suivante :
Théorème.
36 On a
G×H
ind−∞,B (D
]
)=
X
G
ind−∞,B (D
⊗ Wa∗ )χa ,
a∈Ĥ
où
(Wa )a∈Ĥ
est un ensemble de représentants de l'ensemble des classes de
H , χa le caractère
M/H associé à Wa .
repésentations irréductibles unitaires du groupe
Wa ,
et
Wa
est le bré vectoriel au-dessus de
associé à
Nous étudions ensuite la propriété de multiplicativité. Considérons deux
(M, F) et (M 0 , F 0 ) munies d'action feuilletées de G et H respectivement. Si A est un opérateur
(G, F)-transversalement elliptique agissant sur M et B est un opérateur
(H, F 0 )-transversalement elliptique agissant sur M 0 alors ces deux opérateurs
0
0
induisent un opérateur G × H -invariant F ⊕ F -basique A]B sur M × M
0
qui est (G × H, F ⊕ F )-transversalement elliptique. De plus l'indice de A]B
variétés fermées munies de feuilletages riemanniens
se calcule comme suit :
9
Théorème.
37
G×H
ind−∞,B (A]B)
G×H
= indG
−∞,B (A)ind−∞,B (B).
Supposons maintenant qu'on a une variété non-compacte
U
munie d'un
G et une variété compacte M vériant
j:U →M
respectant les feuilletages et les actions de groupes. Si D est un opérateur
diérentiel (G, F)-transversalement elliptique sur U , vériant une certaine
hypothèse, on peut alors dénir le poussé-en-avant j∗ (D) et on a :
feuilletage et d'une action feuilletée de
les mêmes hypothèses. On suppose de plus qu'on a un plongement
Théorème.
G
38 L'indice distributionnel basique ind−∞,B (j∗ (D)) est indé-
pendant du choix de
j.
Dans la dernière partie de cette thèse, nous suivons une méthode classique en géométrie des feuilletages et appliquons le théorème de structure des
feuilletages riemanniens dû à P. Molino [Mol88]. Nous utilisons donc le théorème de Molino an de calculer l'indice distributionnel basique d'un opéra-
D qui est (G, F)-transversalement elliptique en fonction de l'indice équivariant d'un opérateur D̄ sur la variété basique qui est G-transversalement
elliptique. Lorsque G est le groupe trivial, cette construction a été réalisée
teur
dans [EKA90], l'utilisation de l'indice distributionnel permet alors de généraliser cette approche. Plus précisément nous démontrons :
Théorème.
40 L'indice distributionnel basique de
G
ind−∞,B (D)
où
H
D
est donné par
H
= indG
−∞ (D̄ )
désigne le groupe orthogonal et
D̄H
H(G × H)-invariant
est la restriction aux sections
invariantes d'un certain opérateur diérentiel elliptique
sur la variété basique.
La thèse est structurée de la manière suivante.
Dans la première partie nous donnons les rappels nécéssaires sur les opérateurs diérentiels elliptiques. Puis nous étudions le cas des opérateurs invariants par rapport à l'action d'un groupe de Lie compact. Ces résultats
sont classiques et sont rappelés pour le confort du lecteur.
Dans la deuxième partie nous nous concentrons sur les feuilletages riemanniens. Nous dénissons les outils nécessaires à leur étude comme la
connexion de Levi-Civita transverse et la forme de courbure principale. Nous
dénissons ensuite la cohomologie basique.
Le but de la troisième partie est l'étude des opérateurs transversalement
elliptiques au feuilletage. Nous suivons l'article d'A. El-Kacimi [EKA90] pour
montrer que de tels opérateurs ont des propriétés similaires aux opérateurs
10
diérentiels elliptiques sur les variétés fermées. Nous étudions ensuite les opérateurs diérentiels classiques comme le Laplacien basique et décrivons des
propriétés classiques de la cohomologie basique. Nous calculons également
des exemples d'indices d'opérateurs transversalement elliptiques et terminons par étudier l'invariance par homotopie feuilletée de la signature basique.
La quatrième partie est dédiée à la situation d'un feuilletage riemannien
muni d'une action d'un groupe de Lie compact
G
respectant le feuilletage.
Nous nous intéressons alors aux opérateurs transversalement elliptiques par
rapport au feuilletage et à l'action du groupe. Nous montrons que les opérateurs de ce type admettent un indice basique distributionnel (théorème 35)
et établissons les propriétés de cet indice. A l'aide du théorème de Molino,
nous montrons alors (théorème 40) qu'on peut ramener ce problème à celui
d'un opérateur transversalement elliptique par rapport au produit cartésien
de
G et d'un groupe orthogonal, et établissons ainsi le lien entre le problème
de l'indice basique et le problème de l'indice équivariant (théorème 40).
Une question naturelle qui pourrait prolonger cette thèse est par exemple
l'adaptation du travail de Berline et Vergne an d'obtenir une formule de
délocalisation pour calculer l'indice distributionnel basique.
L'annexe A introduit les premières notions sur les feuilletages et rappelle
les deux théorèmes de structure sur les feuilletages riemanniens dûs à P.
Molino [Mol88].
L'annexe B rappelle la notion de
F -bré
11
vectoriel [KT75].
Chapitre 2
Rappels sur les opérateurs
diérentiels
Soient
(M, g)
une variété compacte connexe riemmanienne sans bord
(x1 , ..., xn ), et E, E 0 des 0
brés vectoriels hermitiens au-dessus de M de rang N et N . On notera Ξ(M )
l'algèbre de Lie des champs de vecteurs sur M , h., .ig le produit scalaire ponc2
tuel associé à la métrique g , h., .iM le produit scalaire L ou h., .i s'il n'y a
M
pas d'ambiguïté et ∇
la connexion de Levi-Civita sur M .
orientée de dimension
n
de coordonnées locales
2.1 Opérateurs diérentiels
Nous allons commencer par rappeler quelques éléments de la théorie des
opérateurs diérentiels elliptiques, en particulier le fait que de tels opérateurs admettent un indice de Fredholm (voir [AS68, Gil84, LM89, Roe98])
et étudier un peu plus en détails les opérateurs diérentiels provenant de
situations géométriques : le Laplacien, l'opérateur de de Rham, l'opérateur
de signature, l'opérateur de Dolbeault et l'opérateur de Dirac.
2.1.1 Opérateurs diérentiels elliptiques
Dans tout le paragraphe nous rappellerons les diérents théorèmes sans
donner de démonstration. Le lecteur intéressé trouvera les diérentes démonstrations dans [LM89].
Dénition 1.
On appelle opérateur diérentiel d'ordre
plication linéaire
D : Γ(E) → Γ(E 0 )
tel que
D
forme
D=
X
aα (x)Dα
|α|≤m
12
m
sur
M
une ap-
s'écrit localement sous la
où
Dα = i|α|
Remarque.
aα (x)
taille
∂α
∂xα1 1 ...∂xαnn
aα (x) ∈ hom(Ex , Ex0 ).
En utilisant des trivialisations locales on peut voir localement
comme un élément de
N×
MN,N 0 (C ∞ (M ))
C ∞ (M ).
l'ensemble des matrices de
N 0 à coecients dans
Dénition 2.
ξ
et
x ∈ M et ξ ∈ Tx∗ M , le symbole principal
0
linéaire σ(D)(x, ξ) : Ex → Ex dénie par
X
ξ1α1 ...ξnαn aα (x).
σ(D)(x, ξ) = im
Soient
est l'application
de
D
en
x
et
|α|=m
Remarque.
On note
π : T ∗M → M
la projection.
D est une section du bré hom(π ∗ (E), π ∗ (E 0 )) au-dessus
σ(D)(x, ξ) est un polynôme homogène de degré m par
variable ξ .
Alors le symbole de
∗
de T M . Le symbole
rapport à la
Dénition 3.
tout co-vecteur non-nul
Exemple 1.
d :
D est elliptique si pour
σ(D)(x, ξ) est inversible.
On dit que l'opérateur diérentiel
ξ∈
T ∗ M \{0} le symbole
Il est facile de voir que la diérentielle de de Rham
Ωk (M )
symbole
→ Ωk+1 (M ) est un opérateur diérentiel d'ordre
k ∗
est donné par σ(d)(x, ξ)(ω) = iξ ∧ ω où ω ∈ Λ Tx M .
Dénition 4.
nienne
munit
1 et que son
Soit dvol la forme volume canonique sur la variété rieman-
M . Si h est une métrique hermitienne sur
Γ(E) du produit scalaire déni par
Z
σ, σ 0 =
h(σ, σ 0 )dvol.
le bré vectoriel
E,
on
M
On appelle adjoint formel de
D
l'opérateur
D∗ : Γ(E 0∗ ) → Γ(E ∗ ) caractérisé
par
Proposition 1.
Soit
D(σ), σ 0 = σ, D∗ (σ 0 ) .
D : Γ(E) → Γ(E 0 )
un opérateur diérentiel d'ordre
∗
∗
et D son adjoint formel. Alors D est un opérateur diérentiel d'ordre
∗
∗
∗
et le symbole de D est donné par σ(D )(x, ξ) = σ(D)(x, ξ) .
En particulier
Exemple 2.
D
est elliptique si et seulement si
On notera
δ
D∗
m
m
est elliptique.
l'adjoint formel de la diérentiel de de Rham
d.
Rappelons qu'avec les conventions de signe habituelles,
δ : Ωk (M ) → Ωk−1 (M )
est donné par
δ = (−1)nk+n−1 ∗ d∗,
M (voir [LM89]).
∆ = dδ + δd : Ω∗ (M ) → Ω∗ (M )
où
∗
désigne
l'opérateur de Hodge sur
Le Laplacien
est un opérateur diérentiel
d'ordre 2.
De plus son symbole est donné par
σ(∆)(x, ξ) =
n
X
ξj2 = ||ξ||2 Id.
j=1
En particulier le Laplacien est un opérateur elliptique.
13
Exemple 3.
L'opérateur
2
Comme D
On note
Ωpair = ⊕k pair Ωk (M )
Ωimpair = ⊕k impair Ωk (M ).
∗
diérentiel d'ordre 1 sur Ω (M ).
et
D = d + δ est un opérateur
= ∆, on voit que D est un opérateur
elliptique.
Dans la suite on appellera opérateur de de Rham l'opérateur
D+ : Ωpair → Ωimpair
Dénition 5.
On appelle
qui est la restriction de l'opérateur
Soient
s-ième
∇
E
une connexion linéaire sur
et
D
à
Ωpair (M ).
s ∈ N.
norme de Sobolev (associée à la connexion
E)
métrique hermitienne sur
∇
et à la
la norme
||σ||2s
s
X
=
||∇j (σ)||2
j=0
où
||.||
est la norme induite par la métrique sur
On appelle
s-ième
E.
de Γ(E)
et
espace de Sobolev la complétion
de Sobolev. On le notera
Remarque.
M
pour la norme
H s (E).
On peut montrer que la dénition des espaces de Sobolev est
indépendante du choix de la métrique et de la connexion (voir [LM89]).
On rappelle que la variété
Théorème 1
M
est supposée compacte.
.
Soit
s>
s0 < s
on a
(d'inclusion de Sobolev)
s
continue H (E)
⊂
C k (E).
Théorème 2 (Lemme de Rellich).
Si
n
+ k,
2
on a une inclusion
0
H s (E) ⊂ H s (E).
De plus
l'inclusion est dense et compacte.
Proposition 2.
alors
D
se prolonge
Théorème 3.
d'ordre
D : Γ(E) → Γ(E 0 ) un opérateur diérentiel d'ordre m,
s
s−m (E 0 ), ∀s ∈ N.
en un opérateur borné D : H (E) → H
Soit
Soit
D : Γ(E) → Γ(E 0 )
un opérateur diérentiel elliptique
m.
(i) Si U est un ouvert de
C ∞ implique que
σ|U
M
σ ∈ H s (E), alors D(σ)|U est de
∞ (régularité elliptique).
classe C
et
est de
s ∈ N, D se prolonge en un opérateur de Fredholm
D : H s (E) → H s−m (E 0 ) dont l'indice de Fredholm déni
classe
(ii) Si
ind(D)
est indépendant de
quement l'action de
par
= dim ker D − dim ker D∗
s. De plus on calcule cet indice
D sur les sections C ∞ de E .
en regardant uni-
Le lecteur trouvera les preuves des diérents points du théorème suivant
dans [LM89, Gil84].
Théorème 4.
formellement
D : Γ(E) → Γ(E) un opérateur
auto-adjoint d'ordre m > 0. Alors
Soit
14
diérentiel elliptique
(i) Les valeurs propres de
(ii) Les espaces propres de
D sont réelles.
D sont de dimension nie et formés de sections
C ∞.
D est une suite qui tend en module
+∞ (autrement dit D est un opérateur à résolvante compacte).
2
(iv) L (M, E) est la somme hilbertienne des espaces propres de D .
m
(v) Si (λk )k est la suite des valeurs propres de D on a λk ∼ ck n où c est
(iii) L'ensemble des valeurs propres de
vers
une constante.
Théorème 5.
formellement
D : Γ(E) → Γ(E) un opérateur diérentiel elliptique
2
auto-adjoint d'ordre m. Alors on a une décomposition L Soit
orthogonale
Γ(E) = ker D ⊕ ImD.
Exemple 4.
alors
E = ΛT ∗ M et D est le Laplacien ∆,
∗
∗
Im∆ = Imd ⊕ Imd et ker ∆ = H (M ) est l'ensemble
Si
des formes har-
moniques. On obtient alors la décomposition de de Rham-Hodge :
Ωp (M ) = Hp (M ) ⊕ Imd ⊕ Imd∗ .
Corollaire 1.
La cohomologie de de Rham
des formes harmoniques
H ∗ (M ) est isomorphe à l'espace
H∗ (M ).
Nous rappelons ici cette démonstration car elle nous sera utile par la
suite.
Démonstration.
Ω∗ (M )
et Imδ
Donc
Donc
Selon la décomposition de de Rham-Hodge on a
= H∗ (M ) ⊕ Imd ⊕ Imδ où
∼ (ker d)⊥ .
H∗ (M ) = {ω ∈ Ω∗ (M )/dω = 0
et
δω = 0}
=
ker d = H∗ (M ) ⊕ Imd, puisque d2 = 0.
H ∗ (M ) = ker d/Imd ∼
= H∗ (M ).
Exemple 5.
Dans le cas de l'opérateur de de Rham
χ(M ). En eet :
ker D+ = ker ∆|Ωpair , donc le
D+ ,
l'indice de
D+
est
égal à la caractéristique d'Euler
le noyau de
D+
est
noyau de
D+
est l'espace
des formes harmoniques paires.
Or l'espace des formes harmoniques
H∗ (M )
est isomorphe à la cohomologie
∗
de de Rham H (M ).
dim ker D+ = dim H pair (M ).
∗
impair (M ).
même on a dim ker D+ = dim H
Donc
De
Dénition 6.
On suppose ici que
D
Donc ind(D+ )
= χ(M ).
est un opérateur diérentiel elliptique
m > 0, on peut alors dénir par
s ∈ R (voir [Gil84]) : si λ est une valeur
−s (v) = λ−s v , si
propre non-nulle et v un vecteur propre associé on pose D
−s
λ = 0 et v est un vecteur propre associé on pose D (v) = 0.
formellement auto-adjoint positif d'ordre
calcul fonctionnel l'opérateur
D−s
où
15
Citons un dernier résultat, dont le lecteur intéressé touvera la preuve
dans [Gil84].
Théorème 6.
Sous les mêmes, hypothèse, on note
pace propre associé à
Si
s>
dim M
,
m
alors
dλ
la dimension de l'es-
λ.
D−s
est traçable et
trD−s =
X dλ
λ>0
λs
.
2.1.2 L'opérateur de signature
Supposons que
Rappel.
M
est orientée sans bord et de dimension
L'application
Q : H 2l (M ) × H 2l (M ) dénie
Z
0
ω ∧ ω0
Q([ω], [ω ]) =
n = 4l.
par
M
est une forme bilinéaire bien dénie, symétrique et non-dégénérée.
σ(M )
On note
Dénition 7.
sa signature, appelée la signature de
On note
τ : Ωk (M ) → Ωn−k (M )
τ = (−1)l+
où
∗
k(k−1)
2
M.
l'application dénie par
∗
désigne l'opérateur de Hodge.
Proposition 3.
l'opérateur
L'application
τ
est une involution qui anticommute avec
D = d + δ.
Démonstration.
δ = (−1)nk+n−1 ∗d∗ où ∗ désigne l'opérateur
2
k
Donc ici δ = − ∗ d∗ et ∗ = (−1) Id, et τ
On rappelle que
∗2 = (−1)k(n−1) .
anticommute avec D .
de Hodge et
Dénition 8.
∗
∗
∗
∗
On note Ω (M ) = Ω+ (M ) ⊕ Ω− (M ) où Ω+ (M ) (respective∗
ment Ω− (M )) est l'espace propre de τ associé à la valeur propre 1 (respec-
tivement
−1).
On appelle opérateur de signature et on note
D+
la restriction de
D
à
Ω∗+ (M ), D+ : Ω∗+ (M ) → Ω∗− (M ).
Proposition 4.
signature
σ(M )
Démonstration.
L'indice de Fredholm de l'opérateur de signature
de la variété
D+
est la
M.
On rappelle que l'espace
H∗ (M )
des formes harmoniques
∗
est isomorphe à H (M ).
Comme
τ
involution
anticommute avec
τ : ker D → ker D
D et commute avec ∆, τ
τ : ker ∆ → ker ∆.
et
On a donc les décompositions
∗
∗
H∗ (M ) = H+
(M ) ⊕ H−
(M )
16
se restreint en une
∗
∗
H ∗ (M ) = H+
(M ) ⊕ H−
(M ).
∗ (M ) − dim H∗ (M ) = dim H ∗ (M ) − dim H ∗ (M ).
= dim H+
−
+
−
∗
∗
k
4l−k (M )) ⊕ H2l (M ),
Or H+ (M ) = ⊕k<2l H+ (M ) ∩ (H (M ) ⊕ H
+
∗
∗
k
4l−k (M )) ⊕ H2l (M ).
et H− (M ) = ⊕k<2l H− (M ) ∩ (H (M ) ⊕ H
−
k
4l−k (M ) où k ∈ {0, ..., 2l − 1}.
Soit Vk l'espace H (M ) ⊕ H
k
4l−k
Alors H (M ) et H
(M ) sont permutés par l'action de τ .
Donc ind(D+ )
Donc
τ
agit sur
Vk
et
τ
s'écrit sous la forme
0 1
.
1 0
Donc l'espace propre associé à 1 est l'ensemble des éléments de la forme
(ω, τ (ω)).
dim H k (M ).
k
-1 est dim H (M ).
Donc la dimension de l'espace propre associé à 1 est
De même la dimension de l'espace propre associé à
Donc
∗
∗
dim(⊕k<2l H+
(M )∩(Hk (M )⊕H4l−k ))−dim(⊕k<2l H−
(M )∩(Hk (M )⊕H4l−k )) = 0,
2l (M ) − dim H 2l (M ).
= dim H+
−
2l (M ) et β ∈ H 2l (M )
τ = ∗ sur H 2l (M ), donc si α ∈ H+
−
Z
Q(α, α) =
α∧α
ZM
=
α ∧ τ (α)
M
Z
=
α ∧ ∗α
et ind(D+ )
Or
on a :
M
= hα, αiM > 0
Donc
Q(α, α) > 0.
De même
Z
β∧β
Q(β, β) =
ZM
−β ∧ τ (β)
=
MZ
=−
β ∧ ∗β
M
= − hβ, βiM < 0
Donc
Q(β, β) < 0.
Donc par dénition de la signature d'une forme bilinéaire on a
ind(D+ )
= σ(Q).
2.1.3 L'opérateur de Dolbeault
Supposons à présent que la variété
M
est munie d'une structure com-
plexe. Les premiers résultats de ce paragraphe sont supposés relativement
17
connus, nous omettons donc les démonstrations et renvoyons le lecteur à la
référence [Wel80].
Dénition 9.
T MC = T M ⊗ C, on note J
On note
l'automorphisme associé
à la structure complexe.
Comme
J 2 = −Id
on a une décomposition en somme directe
T MC = T M(1,0) ⊕ T M(0,1)
où
−i
T M(1,0)
de J .
et
T M(0,1)
sont les sous-brés associés aux valeurs propres
i
et
On a alors une décomposition du bré en algèbres extérieures
Λk T ∗ MC = ⊕r+s=k Λr,s
Dénition 10.
type
où
Λr,s = Λr T ∗ M(1,0) ⊗ Λs T ∗ M(0,1) .
Une section de
Λr,s
est appelée une forme diérentielle de
(r, s).
On notera
Ωr,s (M, C)
(r, s).
l'espace des formes diérentielles de type
k
r,s
On a de manière évidente Ω (M, C) = ⊕r+s=k Ω (M, C).
k
Sur Ω (M, C) la diérentielle de de Rham se décompose en la somme de
deux opérateurs
∂ : Ωr,s (M, C) → Ωr+1,s (M, C)
et
∂¯ : Ωr,s → Ωr,s+1 (M, C)
vériant les relations :
∂ 2 = 0, ∂¯2 = 0,
et
¯ = 0.
∂ ∂¯ + ∂∂
On obtient donc un complexe diérentiel pour tout
∂¯
...
- Ωr,s (M, C)
∂¯ -
r≥0
Ωr,s+1 (M, C)
:
∂¯
- ...
appelé complexe de Dolbeault. La cohomologie associée sera appelée cohomologie de Dolbeault et notée
Proposition 5.
∗:
H r,s (M, C).
L'opérateur de Hodge induit un isomorphisme
Ωr,s (M, C)
00
On pose δ
→ Ωq−r,q−s (M, C).
¯ , alors δ 00 est
= − ∗ ∂∗
Proposition 6.
rateur
∆00
On notera
∆00
l'adjoint formel de
l'opérateur déni par
∂¯.
¯ 00 . L'opé∆00 = δ 00 ∂¯ + ∂δ
est un opérateur diérentiel d'ordre 2 auto-adjoint et elliptique.
Démonstration.
Cette preuve est similaire au cas du Laplacien, nous l'omet-
trons donc.
Théorème 7.
On note
¯ =0
Hr,s (M, C) = {ω ∈ Ωr,s (M )/∂ω
On a les propriétés suivantes :
18
et
δ 00 ω = 0} = ker ∆00 .
Hr,s (M, C) est de dimension
2
décomposition L -orthogonale
(i) l'espace vectoriel
(ii) on a une
nie,
¯ ⊕ Im(δ 00 ).
Ωr,s (M, C) = Hr,s (M, C) ⊕ Im(∆00 ) = Hr,s (M, C) ⊕ Im(∂)
(ii) l'espace vectoriel
H r,s (M, C)
est isomorphe à
Hr,s (M, C)
et donc de
dimension nie.
Démonstration.
Il sut d'appliquer les théorèmes 4 (page 14) et 5 (page
15) pour les deux premiers points. La démonstration du troisième point est
similaire au cas de la cohomologie de de Rham.
Dénition 11.
...
A partir du complexe de Dolbeault
∂¯
∂¯ -
- Ω0,s (M, C)
on construit l'opérateur de Dolbeault
∂¯
Ω0,s+1 (M, C)
DDol
- ...
déni par
DDol = ∂¯ + ∂¯∗ : Ω0,pair → Ω0,impair .
Proposition 7.
L'opérateur de Dolbeault possède un indice de Fredholm
donné par
ind(DDol )
=
n
X
(−1)k dim H 0,k (M, C).
k=0
Démonstration.
On a
2
= ∆00 ,
DDol
et
∆00
est elliptique donc
DDol
est ellip-
tique et possède un indice.
Le calcul de l'indice est similaire au calcul de l'indice de l'opérateur de de
Rham (voir l'exemple 5).
2.1.4 L'opérateur de Dirac
Nous allons à présent rappeler la construction et les propriétés de l'opérateur de Dirac et voir le lien avec les opérateurs dénis précédemment (voir
par exemple [LM89, Gil84, Roe98]).
Notation 1.
au-dessus de
On note
M
Dénition 12.
et
∇M
Cl(M ) = Cl(T M ) ⊗ C
le bré en algèbre de Cliord
la connexion de Levi-Civita sur
Cl(M )-modules au-dessus de M , h une
métrique hermitienne sur E
E.
On note l'action de ξ ∈ Cl(Tx M ) sur un élément v ∈ Ex par c(ξ)v .
E
On dit que (E, h, ∇ ) est un bré de Cliord si :
E
(i) La connexion ∇ est une connexion métrique.
(ii) Pour tout ξ ∈ Cl(Tx M )), c(ξ) est antisymétrique c'est-à-dire
Soient
E
M.
un bré en
E
et ∇ une connexion linéaire sur
h(c(ξ)s1 , s2 ) = −h(s1 , c(ξ)s2 ), ∀s1 , s2 ∈ Γ(E).
19
∇E vérie [∇E , c] = 0 où [∇E , c] = ∇E c−c∇M , c'est-à
X ∈ Ξ(M ), Y ∈ Ξ(M ), s ∈ Γ(E),
(iii) La connexion
dire si
M
E
∇E
X (c(Y )s) = c(∇X (Y ))s + c(Y )∇X (s).
Notation 2.
Dans la suite
Dénition 13.
(E, h, ∇E )
désigne un bré de Cliord.
On appelle opérateur de Dirac l'opérateur noté
D
obtenu à
partir de la composition des applications suivantes :
∇E
Γ(E)
- Γ(T ∗ M ⊗ E)
Plus précisément si
{e1 , ..., en }
∼
=-
c
Γ(T M ⊗ E)
- Γ(E)
est un repère local orthonormé de
D=
n
X
TM
on a
c(ej ) ◦ ∇E
ej .
j=1
Proposition 8.
L'opérateur de Dirac est un opérateur diérentiel elliptique
d'ordre 1. De plus son symbole est donné par
σ(D)(x, ξ) = ic(ξ).
Démonstration.
x ∈ M, {e1 , ..., en }
(x1 , ..., xn ) des
∂
.
coordonnées locales en x tel que x correspond à 0 et ej à
∂xj
Au travers l'identication Tx M ∼
= Tx∗ M , ej correspond à dxj .
E
En utilisant des trivialisations locales autour de x, on peut écrire ∇e comme
j
∂
la somme de
et d'un opérateur diérentiel d'ordre 0.
∂xj
n
X
∂
Donc au voisinage de x, on peut écrire D comme la somme de
c(ej )
∂xj
Soit
une base de
Tx M
et
j=1
et d'un opérateur diérentiel d'ordre 0.
Donc
D
est bien un opérateur diérentiel d'ordre 1. Si
vecteur non-nul,
ξ=
n
X
ξj dxj .
n
X
c(ej )ξj = ic(
ej ξj ) = ic(ξ).
σ(D)(x, ξ) = i
Donc
σ(D2 )(x, ξ) = c(ξ)2 = ||ξ||2
j=1
j=1
(par dénition de la multiplication de
Cliord).
D2
et
D
est un co-
j=1
n
X
Donc
Donc
ξ ∈ Tx∗ M
sont elliptiques.
20
Rappel.
Rappelons qu'on a les formules
d=
n
X
ej ∧ ∇ M
ej
et
j=1
δ = d∗ = −
n
X
iej ∇M
ej
(voir [LM89]).
j=1
Proposition 9.
Démonstration.
et
L'opérateur de Dirac
Soient
s1 , s2 ∈ Γ(E).
{e1 , ..., en }
D
est formellement auto-adjoint.
un repère local orthonormé de
TM
On a ponctuellement
h(D(s1 ), s2 )x − h(s1 , D(s2 ))x
=
=
q
X
j=1
q
X
E
h(c(ej )∇E
ej (s1 ), s2 )x − h(s1 , c(ej )∇ej (s2 ))x
E
h(c(ej )∇E
ej (s1 ), s2 )x + h(c(ej )s1 , ∇ej (s2 ))x
j=1
=
q
X
M
h(∇E
ej (c(ej )s1 ), s2 )x − h(c(∇ej (ej ))s1 , s2 )x
j=1
+ h(c(ej )s1 , ∇E
ej (s2 ))x
q
q
X
X
=(
∇M
(h(c(e
)s
,
s
))
)
−
h(c(
∇M
j 1 2 x
ej
ej (ej ))s1 , s2 )x
j=1
q
X
=−
j=1
∇M
ej (iej ω)x + ω(
j=1
où
ω
q
X
∇M
ej (ej ))x
j=1
est la 1-forme dénie par
ω(X) = −h(c(X)s1 , s2 ), ∀X ∈ Ξ(M ).
h(D(s1 ), s2 ) − h(s1 , D(s2 )) = −
q
X
∇M
ej (iej ω) + ω(
j=1
=−
=−
q
X
j=1
q
X
q
X
Donc
∇M
ej (ej ))
j=1
q
X
(iej ∇M
+
i
)ω
+
ω(
∇M
M
∇e (ej )
ej
ej (ej ))
j
j=1
iej ∇M
ej ω
j=1
= δω
Z
Z
h(D(s1 ), s2 ) − h(s1 , D(s2 ))dvol =
Donc
M
δω dvol où dvol désigne la forme
M
volume canonique.
Donc
Donc
hD(s1 ), s2 i − hs1 , D(s2 )i = hδω, 1i = hω, d1i = 0.
D est formellement auto-adjoint.
21
Proposition 10. Si E est le bré tangent T M on a un isomorphisme naturel
Cl(T M ) ∼
= ΛT ∗ M ([LM89])
conjugué à d + δ .
2
particulier D est conjugué au Laplacien ∆.
de brés vectoriels
est
En
Démonstration.
Au travers de
{e1 , ..., en } un repère local orthonormé.
l'identication Cl(M ) ∼
= ΛT ∗ M l'élément c(e)ω
D
Soit
e ∧ ω − ie ω .
n
X
Or d =
ej ∧ ∇ M
ej
et
δ = d∗ = −
j=1
Donc
et l'opérateur de Dirac
n
X
devient
iej ∇M
ej .
j=1
n
X
d+δ =
(ej ∧ . − iej )∇M
ej
est conjugué à
j=1
n
X
c(ej )∇M
ej
c'est-à-dire à
j=1
l'opérateur de Dirac.
(d + δ)2 = d2 + dδ + δd + δ 2 . Comme d2 = δ 2 = 0,
2
Donc D est conjugué au Laplacien ∆.
Or
Remarque.
En munissant
Cl(T M )
on a
(d + δ)2 = ∆.
des bonnes graduations (voir [LM89])
on retrouve ainsi l'opérateur de de Rham et l'opérateur de signature à l'aide
de l'opérateur de Dirac.
2.2 Actions de groupes compacts
Nous allons à présent étudier le cas où notre variété est munie d'une action de groupe. Dans un premier temps nous étudions la cohomologie de de
Rham invariante, puis nous verrons que pour les opérateurs que nous avons
étudiés précédemment, nous pouvons dénir un indice en tant que représentation. Nous nissons par donner la formule d'Atiyah-Singer qui permet de
calculer cet indice dans le cas des opérateurs de signature et de Dolbeault.
2.2.1 Cohomologie de de Rham invariante
Soit
M
une variété compacte connexe munie d'une action lisse d'un
groupe de Lie compact
On munit
M
G.
d'une structure riemannienne
G-invariante
et on munit
G
la mesure de Haar normalisée.
Dénition 14.
Soit
Notation 3.
E
ω ∈ Ω∗ (M ).
∗
On dit que ω est G-invariante si ∀g ∈ G, on a g (ω) = ω .
∗
On notera Ω (M/G) l'ensemble des forme diérentielles G-invariantes.
∗
On voit immédiatement que Ω (M/G) est une algèbre diérentielle
Z2 -graduée et un C ∞ (M/G)-module.
∗
On note H (M/G) la cohomologie des formes diérentielles invariantes.
Γ(M, E/G)
Si
est un
G-bré
vectoriel au-dessus de
∞
le C (M/G)-module des sections
22
M,
on notera
G-invariantes.
de
Proposition 11.
]
une application i
On note
:
i : Ω∗ (M/G) → Ω∗ (M )
→ H ∗ (M ) .
l'inclusion, alors
i
induit
H ∗ (M/G)
Démonstration.
En eet on a
Dénition 15.
L'action de
i(dω) = d(i(ω)),
d'où le résultat.
G sur M induit une action de G sur H ∗ (M ) :
−1 )∗ ([ω]) := [(g −1 )∗ (ω)].
soit g ∈ G, on pose g.([ω]) = (g
∗
G
∗
On note H (M ) le sous-espace vectoriel de H (M ) des classes de cohomologie invariantes.
Proposition 12.
On note
M
l'application
M : Ω∗ (M ) → Ω∗ (M/G)
dénie
par
Z
M (ω) =
g ∗ (ω)dg.
G
∀ω ∈ Ω∗ (M ), M (dω) = d(M (ω)).
]
∗
∗
En particulier M induit une application M : H (M ) → H (M/G).
Z
Démonstration. Remarquons que g∗ (ω)dg est bien G-invariante.
Alors
G
Z
M (dω) =
ZG
=
g ∗ (dω)dg
dg ∗ (ω)dg
GZ
= d(
g ∗ (ω)dg)
(dérivation sous le signe somme)
G
= d(M (ω)).
Proposition 13.
On a
i] (H ∗ (M/G)) ⊂ H ∗ (M )G
]
]
i ◦M ∗
= IdH ∗ (M )G et M ] ◦ i] = Id|H ∗ (M/G)
|H (M )G
∗
G ∼ H ∗ (M/G). On obtient donc que H ∗ (M/G) s'idenC'est-à-dire H (M )
=
∗
∗
tie à un sous-espace de H (M ) et comme M est compacte, H (M/G) est
de dimension nie.
Démonstration.
Soit
[ω] ∈ H ∗ (M/G),
[ω] car ω ∈ Ω∗ (M/G),
∗
∗
on a g ([ω]) = [g (ω)] =
]
∗
G
donc i ([ω]) ∈ H (M ) .
[ω] ∈ H ∗ (M )G , c'est-à-dire g ∗ ([ω]) = [ω],
∗
∗
∗
donc [g (ω) − ω] = 0 et g (ω) − ω = dβg où βg ∈ Ω (M ) (comme
∞
l'action de G sur M est C , on voit facilement qu'on peut choisir βg
∞ de g ).
de manière à ce que βg dépende de manière C
Z
Z
Z
Soit
g ∗ (ω)dg − ω =
Donc
G
dβg dg = d
G
βg dg
G
23
.
Z
∗
g (ω)dg = [ω],
Donc
G
]
Donc M ([ω])
Notation 4.
= [ω]
On note
Proposition 14.
Si
g]
G
et
c'est-à-dire
[M (ω)] = [ω].
i] (M ] ([ω])) = [ω].
l'application induite par
est connexe, alors
g∗
sur
H ∗ (M ).
g ] = Id|H ∗ (M ) .
Démonstration.
On emploiera ici la notation φg pour le diéomorphisme sur
g.
∞ tel que γ(0) = e et γ(1) = g .
Soit γ : R → G un chemin C
∞ et H(0, .) = Id
Soit H : R × M → M, (t, x) 7→ φγ(t) (x), alors H est C
M
et H(1, .) = φg .
∗
∗
Donc φe = IdM et φg sont homotopes, donc φg induit l'identité sur H (M ).
]
Donc g = Id|H ∗ (M ) .
M
induit par
Corollaire 2.
Si
Démonstration.
G
G-invariantes,
H ∗ (M/G) ∼
= H ∗ (M ).
δ l'adjoint formel de d.
M , Ω∗ (M/G) est stable par δ .
On note toujours
agit par isométrie sur
On notera alors
En notant
est connexe alors
Découle des deux propositions précédentes.
Proposition 15.
Comme
G
G
D+
la restriction de l'opérateur de de Rham aux formes
c'est-à-dire
χ(M/G) =
G : Ωpair (M/G) → Ωimpair (M/G).
D+
n
X
(−1)k dim H k (M/G),
G
on a ind(D+ )
= χ(M/G).
k=1
G est
de M .
De plus si
d'Euler
Démonstration.
Si
G
G
D+
connexe, l'indice de
est égal à
χ(M )
la caractéristique
La démonstration est similaire au cas général.
est connexe on a vu que
H ∗ (M ) ∼
= H ∗ (M/G),
d'où le résultat.
2.2.2 Opérateurs diérentiels invariants
Dénition 16.
Soit π : G → Gl(V ) une représentation unitaire de dimenG notée (π, V ). On note V G = {x ∈ V /π(g)(x) = x, ∀g ∈ G}
κ(V ) = dim V G .
sion nie de
et
Lemme 1.
Sous les mêmes hypothèses, on a
Z
κ(V ) =
tr(π(g))dg.
G
Démonstration.
Soit
Z
PG
∀x ∈ H, P G (x) =
la projection orthogonale de
π(g)(x)dg .
G
24
V
sur
V G,
alors
Par dénition
P G (x) ∈ V G ,
donc
(P G )2 = P G .
Comme
(π, V )
est unitaire
G est auto-adjoint.
on a que P
Z
Donc
dim P G = tr(P G ) =
tr(π(g))dg
(il sut d'exprimer la trace à l'aide
G
du produit scalaire).
Dénition 17.
Si
[V ] − [V
0]
∈ R(G),
Notation 5.
tation de
On note
on
H
Soient
R(G) l'anneau des représentations de G.
0
0
pose κ([V ] − [V ]) = κ(V ) − κ(V ).
un espace de Hilbert,
π : G → GL(H)
une représen-
G.
Dénition 18.
Soit T ∈ L(H) un opérateur de Fredholm.
G-invariant, alors ker T et ker T ∗ sont des représentations de dimension nie de G.
G
∗
On pose alors ind (T ) = [ker T ] − [ker T ] ∈ R(G).
Si
T
est
Proposition 16.
alors
κ(ind
G
T ∈ L(H) est un opérateur
(T )) = ind(T G ) où T G = T|H G .
Si
de Fredholm
Démonstration.
κ(indG (T )) = dim(ker T )G − dim(ker T ∗ )G
= dim ker T G − dim ker(T G )∗
= ind(T G ).
Dénition 19.
ind
G
Soit g ∈ G, on appelle indice
(T )(g) = tr(π(g)| ker T ) − tr(π(g)| ker T ∗ ).
Proposition 17.
de
g
le réel
Sous les mêmes hypothèses, on a
ind(T
G
Z
)=
ind
G
(T )(g)dg.
G
Démonstration.
ind(T
G
) = κ(indG (T ))
Z
=
tr(πindG (T ) (g))dg
G
Z
=
tr(π(g)| ker T ) − tr(π(g)| ker T ∗ ) dg
ZG
G
=
ind (T )(g)dg.
G
25
G-invariant
2.2.3 L'opérateur de signature invariant
Dénition 20.
On suppose ici que
M
est orientée sans bord de dimension
n = 4l.
On note
QG
la restriction de la forme bilinéaire de signature
G
La signature de Q sera notée
Proposition 18.
Q
à
H 2l (M )G .
σ(M/G).
Sous les mêmes hypothèses, on note
Ω∗ (M/G) = Ω∗+ (M/G) ⊕ Ω∗− (M/G) la décompostion induite par la décom∗
∗
∗
G
position Ω (M ) = Ω+ (M )⊕Ω− (M ) et D+ la restriction de l'opérateur de siG
∗
∗
gnature aux formes G-invariantes, c'est-à-dire D+ : Ω+ (M/G) → Ω− (M/G).
G
G
Alors ind(D+ ) = σ(M/G). De plus si G est connexe alors ind(D+ ) = σ(M ).
Démonstration.
Si
G
La démonstration est similaire au cas général.
est connexe on a vu que
H ∗ (M ) ∼
= H ∗ (M/G),
d'où le résultat.
Dénition 21.
H 2l (M ),
On pose
Sous les mêmes hypothèses, le groupe de Lie G agit sur
H 2l (M ) est une représentation de dimension nie de G.
G
2l
2l
ind (D+ ) := [H+ (M )] − [H− (M )] ∈ R(G) où D+ désigne l'opéradonc
teur de signature.
Proposition 19.
Sous les mêmes hypothèses, on a
G
κ(indG (D+ )) = ind(D+
) = σ(M/G).
Démonstration.
Corollaire 3.
C'est une conséquence de la proposition 17 (page 25).
∗
trivialement sur H (M ), donc
Démonstration.
G est connexe alors G
ind (D+ )(g) = σ(M ).
Sous les mêmes hypothèses, si
∀g ∈ G,
on a
agit
G
G
(D+ )(g) = χindG (D+ ) (g) où χindG (D+ )
G
2l
2l
ractère de la représentation ind (D+ ) = [H+ (M )] − [H− (M )].
∗
Or G agit trivialement sur H (M ),
2l
2l
donc χindG (D ) (g) = dim H+ (M ) − dim H− (M ).
+
G
Donc ind (D+ )(g) = σ(M ).
On a ind
est le ca-
Nous allons à présent rappeler la formule d'Atiyah-Segal-Singer pour la
G-signature
M.
[AS68]. On supposera que le groupe
G
préserve l'orientation de
Proposition 20. Soit g ∈ G, on note M g l'ensemble des points xes de g sur
M.
Alors
Mg
est une sous-variété compacte sans bord de
de dimension non constante en général).
Démonstration.
Voir [LM89] par exemple.
26
M
(non connexe,
Proposition 21.
c'est-à-dire
G
Comme
∀x ∈
g ∈ G et N g le bré normal au-dessus
= (Tx M g )⊥ .
g
isométries sur M , le bré normal N admet
Soient
de
M g,
M g , Nxg
agit par
une décom-
position
N g = N g (−1) ⊕ ⊕0<θ<π N g (θ)
où
N g (θ)
tivement
N g (−1) sont des sous-brés de N et g∗ agit sur N g (θ) (respecN g (−1)) par une rotation d'angle θ (respectivement par −Id).
et
Dénition 22.
on notera
L
la
Si
E
est un bré vectoriel au-dessus de
L-classe
E
totale de
M g,
qui est dénie à partir des classes de
Pontrjagin par la suite multiplicative :
L(E) =
On notera
mθ (E)
Y
xj
.
th(xj )
la classe caractéristique dénie à partir des classes de
Chern par la suite multiplicative :
mθ (E) =
Y
iθ
)
2
xj + iθ
)
th(
2
th(
( pour plus de détails voir par exemple [AS68, LM89, Hir78, MS74]).
Théorème 8 (formule d'Atiyah-Segal-Singer pour la G-signature).
G,
Soit
alors l'indice équivariant de l'opérateur de signature est donné par :
ind
G
Z
L(g)
(D+ )(g) =
Mg
où
L(g) ∈ H ∗ (M g )
est une classe caractéristique.
Plus précisément on a,
Z
t−r
Z
L(g) = 2
Mg
Mg
Y
(i tan(θ/2))−s(θ) L(M g )
0<θ<π
L(N g (−1))−1 e(N g (−1))
Y
mθ (N g (θ))
0<θ<π
e désigne la classe
s(θ) = dimC N g (θ).
où
Corollaire 4.
d'Euler,
2t = dim M g , 2r = dim N g (−1)
G
Z Z
On a alors ind(D+ )
Démonstration.
G
G
En eet ind(D+ )
L(g) dg .
=
Z
=
ind
G
27
Mg
G
(D+ )(g)dg .
et
g∈
2.2.4 L'opérateur de Dolbeault invariant
Nous allons à présent rappeler le théorème de Lefschetz holomorphe
[AS68].
Dénition 23.
Soient
E
On suppose que
M
admet une structure complexe.
un bré vectoriel complexe au-dessus de
E.
Dolbeault DDol
M
et
θ(E)
le faisceau des
germes de sections holomorphes de
On dénit l'opérateur de
associé à
E
à partir du complexe de Dolbeault
:
¯ ∂¯∗
∂+
...
¯ ¯∗
- Λ0,s ⊗ E ∂+∂- Λ0,s+1 ⊗ E
¯ ∂¯∗
∂+
- ...
On suppose qu'on a un groupe ni d'automorphismes agissant sur
M.
Proposition 22.
g
g
Soit g ∈ G, on note N le bré normal au-dessus de M .
g
Comme G agit par isométrie sur M , le bré normal N admet une décomM
g
g
N (θ) où N g (θ) est un sous-bré de N g et g∗ agit sur
postion N =
0<θ6π
N g (θ) par la multiplication par eiθ .
Dénition 24.
Si
E
est un bré vectoriel au-dessus de
M g,
on notera
Uθ
la classe caractéristique dénie à partir des classes de Chern par la suite
multiplicative :
θ
U =
Y 1 − e−xj −iθ −1
1 − e−iθ
j
(pour plus de détails voir par exemple [AS68]).
Théorème 9
(de Lefschetz holomorphe)
.
Soit
g ∈ G,
alors l'indice équiva-
riant de l'opérateur de Dolbeault est donné par :
ind
G
Z
L(g)
(DDol )(g) =
Mg
où
L(g) ∈ H ∗ (M g )
est une classe caractéristique.
Plus précisément on a
Z
Z
L(g) =
Mg
où
Mg
Q
ch(E|M g )(g) 0<θ<π U θ (N g (θ))td(M g )
det(1 − g|(N g )∗ )
ch désigne la classe de Chern totale et td désigne la classe de Todd totale.
De plus l'indice de l'opérateur de Dolbeault est donné par
ind(DDol )
où
χ(M, θ(E)) =
n
X
(−1)k dim H k (M, θ(E)).
k=0
Dans le cas où
E
= χ(M, θ(E))
est le bré trivial
E = M ×C
(page 19).
28
on retrouve la proposition 7
Chapitre 3
Feuilletages riemanniens
On suppose maintenant que la variété
M
est munie d'un feuilletage
F.
3.1 Connexion et courbure
3.1.1 La connexion de Levi-Civita transverse
Nous allons commencer par dénir la connexion de Levi-Civita transverse
(voir [Ton97]) qui joue un rôle similaire à celui de la connexion de Levi-Civita
en géométrie riemannienne.
Dénition 25.
M
νF = T M/T F . On note π : T M → νF la projection
⊥
canonique. On a T M = T F ⊕T F , alors la métrique riemannienne g permet
⊥ tel que
de dénir un isomorphisme de brés vectoriels σ : νF → T F
π ◦ σ = IdνF .
noté
νF
Remarque.
nienne
On appelle bré normal le bré vectoriel au-dessus de
déni par
gνF
On note
sur
νF
Dénition 26.
g = g|T F ⊕ g|T F ⊥ . Alors g induit une métrique riemangνF = σ ∗ (g|T F ⊥ ).
dénie par
On dénit la dérivée de Lie sur
νF
par
∀X ∈ Ξ(M ), ∀s ∈ Γ(νF), LX (s) = π([X, σ(s)]).
On notera encore
extérieurs de
LX
le prolongement de la dérivée de Lie aux puissances
νF .
Dénition 27.
transverse). Si
h une métrique sur νF (h est appelée une métrique
X ∈ Ξ(M ), on note LX (h) le 2-tenseur symétrique sur νF
Soit
déni par
∀s, s0 ∈ Γ(νF), LX (h)(s, s0 ) = X(h(s, s0 )) − h(LX (s), s0 ) − h(s, LX (s0 )).
29
Dénition 28. On dit que la métrique h sur νF est invariante par holonomie
si
∀V ∈ Γ(T F), LV (h) = 0,
autrement dit si
∀V ∈ Γ(T F), ∀s, s0 ∈ Γ(νF)
on a
V (h(s, s0 )) = h(π([V, σ(s)]), s0 )+h(s, π([V, σ(s0 )]) = h(LV (s), s0 )+h(s, LV (s0 )).
On dit que la métrique
sur
νF
g
sur
M
est quasi-brée si la métrique induite par
g
est invariante par holonomie.
Proposition 23.
Le feuilletage
F
est un feuilletage riemannien si et seule-
ment s'il existe une métrique invariante par holonomie sur
Démonstration.
Remarque.
νF .
C'est une reformulation de la proposition 117 (page 119).
F
g
est
On appelle connexion de Bott la connexion partielle sur
νF
Dans la suite on supposera que
est riemmanien et que
quasi-brée.
Dénition 29.
dénie par
˚ X (s) = π([X, σ(s)]) = LX (s), ∀X ∈ Γ(T F).
∀s ∈ νF, ∇
Dénition 30. Soit ∇ une connexion sur νF on dit que ∇ est une connexion
adaptée si
˚V .
∀V ∈ Γ(T F), ∇V = ∇
Proposition 24.
De l'identité de Jacobi, on déduit que la courbure d'une
∇
connexion adaptée
est nulle le long des feuilles :
∀U, V ∈ Γ(T F)
on a
R∇ (U, V ) = ∇U ◦ ∇V − ∇V ◦ ∇U − ∇[U,V ] = 0.
Dénition 31.
On appelle torsion de
∇
la 2-forme
T∇
à valeurs dans
νF
dénie par
T∇ (X, Y ) = ∇X (π(Y )) − ∇Y (π(X)) − π([X, Y ]), ∀X, Y ∈ Ξ(M ).
Proposition 25.
Démonstration.
où
Si
∇
est une connexion adaptée alors
X, Y ∈ Ξ(M ), on
X2 , Y2 ∈ Γ(T F ⊥ ).
Soient
X1 , Y1 ∈ Γ(T F)
et
note
T∇ = 0.
X = X1 + X2
et
Y = Y1 + Y2
T∇ (X, Y )
= T∇ (X1 , Y ) + T∇ (X2 , Y )
= T∇ (X1 , Y ) + T∇ (X2 , Y1 ) + T∇ (X2 , Y2 )
= ∇X1 (π(Y )) − π([X1 , Y ]) + ∇X2 (π(Y1 )) − ∇Y1 (π(X2 )) − π([X2 , Y1 ])
+ ∇X2 (π(Y2 )) − ∇Y2 (π(X2 )) − π([X2 , Y2 ])
= π([X1 , σ(π(Y ))]) − π([X1 , Y ]) + ∇X2 (π(Y1 )) − ∇Y1 (π(X2 )) − π([X2 , Y1 ])
M
+ π(∇M
X2 (Y2 )) − π(∇Y2 (X2 )) − π([X2 , Y2 ])
= −π([Y1 , σ(π(X2 ))]) − π([X2 , Y1 ]) + π(T∇M (X2 , Y2 )) = 0
30
Dénition 32.
on note
Soit ∇ une connexion sur νF et V ∈ Γ(T F), si X ∈ Ξ(M ),
LV (∇)X : Γ(νF) → Γ(νF) l'application linéaire dénie par
LV (∇)X (s) = LV (∇X (s)) − ∇[V,X] (s) − ∇X (LV (s)), ∀s ∈ Γ(νF).
Dénition 33.
∇ une connexion sur νF , on dit que ∇ est invariante
∀V ∈ Γ(T F), on a LV (∇) = 0.
∇ est basique si ∇ est adaptée et invariante par holonomie.
Soit
par holonomie si
On dit que
Proposition 26.
on a
iV (R∇ ) = 0
Démonstration.
∇ une connexion
LV (R∇ ) = 0.
Soit
et
Y ∈ Ξ(M )
Soient
et
basique sur
s ∈ Γ(νF)
νF ,
alors
∀V ∈ Γ(T F)
alors,
R∇ (V, Y )(s) = ∇V ◦ ∇Y (s) − ∇Y ◦ ∇V (s) − ∇[V,Y ] (s)
˚ V ◦ ∇Y (s) − ∇Y ◦ ∇
˚ V (s) − ∇L (Y ) (s)
=∇
V
= LV (∇Y (s)) − ∇Y (LV (s)) − ∇LV (Y ) (s)
= (LV (∇)Y )(s) = 0
Soient
Y, Z ∈ Ξ(M )
et
s ∈ Γ(νF).
On a
LV (R∇ )(Y, Z)(s)
= LV (R∇ (Y, Z)(s)) − R∇ (LV (Y ), Z)(s) − R∇ (Y, LV (Z))(s) − R∇ (Y, Z)(LV (s))
= LV (∇Y ∇Z (s) − ∇Z ∇Y (s) − ∇[Y,Z] (s)) − (∇LV (Y ) ∇Z (s) − ∇Z ∇LV (Y ) (s)
− ∇[LV (Y ),Z]) (s)) − (∇Y ∇LV (Z) (s) − ∇LV (Z) ∇Y (s) − ∇[Y,LV (Z)]) (s))
− (∇Y ∇Z (LV (s)) − ∇Z ∇Y (LV (s)) − ∇[Y,Z] (LV (s)))
= ∇Y (LV (∇Z (s)) − ∇Z (LV (∇Y (s)) − ∇LV ([Y,Z]) (s) + ∇Z ∇LV (Y ) (s)
+ ∇[LV (Y ),Z]) (s) − ∇Y ∇LV (Z) (s) + ∇[Y,LV (Z)]) (s) − ∇Y ∇Z (LV (s)) + ∇Z ∇Y (LV (s))
= (LV (∇Y ∇Z (s)) − ∇LV (Y ) (∇Z (s))) − (LV (∇Z ∇Y (s)) − ∇LV (Z) (∇Y (s)))
− (LV (∇[Y,Z] (s) − ∇[Y,Z] (LV (s)) + ∇Z ∇LV (Y ) (s) + ∇[LV (Y ),Z]) (s)
− ∇Y ∇LV (Z) (s) + ∇[Y,LV (Z)]) (s) − ∇Y ∇Z (LV (s)) + ∇Z ∇Y (LV (s))
= ∇Y (LV (∇Z (s) − ∇LV (Z) (s) − ∇Z (LV (s))) − ∇Z (LV (∇Y (s) − ∇LV (Y ) (s)
− ∇Y (LV (s))) − ∇LV ([Y,Z]) (s) + ∇[LV (Y ),Z] (s) + ∇[Y,LV (Z)] (s)
= −∇LV ([Y,Z]) (s) + ∇[LV (Y ),Z] (s) + ∇[Y,LV (Z)] (s)
= −∇[V [Y,Z]]+[[V,Y ],Z]+[Y,[V,Z]] (s) = 0
Notation 6. On désigne toujours par ∇M la connexion de Levi-Civita.
Dénition 34. On dénit une connexion sur νF par ∇X (s) = π([X, σ(s)]) =
˚ X (s)
∇
si
X ∈ Γ(T F)
et
∇X (s) = π(∇M
X (σ(s)))
31
si
X ∈ Γ(T F ⊥ ).
Remarque.
Comme
∇M
et
˚ sont des connexions, on a bien que ∇ est une
∇
connexion.
Remarque.
Par dénition la connexion
∇
est une connexion adaptée, en
particulier
∀U, V ∈ Γ(T F), R∇ (U, V ) = 0.
˜ une connexion sur νF . On dit que ∇
˜ est une connexion
Dénition 35. Soit ∇
métrique si
˜ X (s), s0 )+gνF (s, ∇
˜ X (s0 )).
∀X ∈ Ξ(M ), ∀s, s0 ∈ Γ(νF), X(gνF (s, s0 )) = gνF (∇
Remarque.
Etant donné la dénition de la connexion
∇
et comme
g
est
quasi-brée on a
∀V ∈ Γ(T F), ∀s, s0 ∈ Γ(νF), V (gνF (s, s0 )) = gνF (∇V (s), s0 )+gνF (s, ∇V (s0 )).
Théorème 10.
La connexion
Démonstration.
Comme
patibilité de
˚T F
∇
métrique puisq'on
∇
est une connexion métrique.
˚ T F + ∇M ⊥ et g = g|T F + g|T F ⊥ , la com∇ = ∇
TF
M
avec g|T F et de ∇
avec g|T F ⊥ entraînent que ∇ est
T F⊥
⊥ et νF . Donc ∇ est une
a un isomorphisme entre T F
connexion métrique.
Théorème 11. La connexion ∇ est l'unique connexion métrique sans torsion
sur
νF .
La connexion
Démonstration.
∇
est appelée connexion de Levi-Civita transverse.
∇ est une connexion
∇ est sans torsion.
s, s0 ∈ Γ(νF), On a
On a vu que
métrique et
∇
est une
connexion adaptée. Donc
Soit
X ∈ Ξ(M ),
et
2gνF (∇X (s), s0 )
= gνF (∇X (s), s0 ) + gνF (∇X (s), s0 )
= X(gνF (s, s0 )) − gνF (s, ∇X (s0 )) + gνF (s0 , ∇X (s))
= X(gνF (s, s0 )) − (gνF (s, ∇σ(s0 ) (π(X)) + π([X, σ(s0 )]))
+ gνF (s0 , ∇σ(s) (π(X)) + π([X, σ(s)]))
= X(gνF (s, s0 )) − (σ(s0 )(gνF (π(X), s)) − gνF (π(X), ∇σ(s0 ) (s)))
− gνF (s, π([X, σ(s0 )])) + (σ(s)(gνF (π(X), s0 )) − gνF (π(X), ∇σ(s) (s0 )))
+ gνF (s0 , π([X, σ(s)]))
= X(gνF (s, s0 )) − σ(s0 )(gνF (π(X), s)) − gνF (s, π([X, σ(s0 )]))
+ σ(s)(gνF (π(X), s0 )) − gνF (π(X), ∇σ(s) (s0 )) + gνF (s0 , π([X, σ(s)]))
+ gνF (π(X), ∇σ(s0 ) (s) − ∇σ(s) (s0 ))
= X(gνF (s, s0 )) − σ(s0 )(gνF (π(X), s)) − gνF (s, π([X, σ(s0 )]))
+ σ(s)(gνF (π(X), s0 )) − gνF (π(X), ∇σ(s) (s0 )) + gνF (s0 , π([X, σ(s)]))
+ gνF (π(X), π([σ(s), σ(s0 )]))
32
de
∇X (s) est uniquement déterminée par la formule ci-dessus, d'où l'unicité
∇.
Théorème 12.
Par conséquent
La connexion
∇
∇
est invariante par holonomie.
est une connexion basique et on a
∀V ∈ Γ(T F), iV (R∇ ) = LV (R∇ ) = 0.
Démonstration.
Nous venons de montrer que la connexion de Levi-Civita
transverse est entièrement déterminée par la métrique
g
qui est quasi-brée
(et donc invariante par holonomie). Par conséquent la connexion
∇
est elle
aussi invariante par holonomie.
3.1.2 Courbure principale
Nous allons à présent dénir la forme de courbure principale du feuilletage
F
(voir [Ton97]).
Notation 7.
On note encore
extérieure associée à
∇
∇ω(X0 , ..., Xr ) =
∇ : Ωr (M, νF) → Ωr+1 (M, νF)
la dérivée
dénie par
r
X
(−1)j ∇Xj (ω(X0 , ..., X̂j , ..., Xp ))
j=0
+
X
(−1)i+j ω([Xi , Xj ], X0 , ..., X̂i , ..., X̂j , ..., Xr )
i<j
où
ω ∈ Ωr (M, νF)
Dénition 36.
valeurs dans
et
Xj ∈ Ξ(M ).
On notera
τ k (M, νF)
l'espace des tenseurs de degré
k
à
νF .
L̃ l'application
∀X, Y1 , ..., Yr ∈ Ξ(M ),
On note
linéaire
L̃ : Ωr (M, νF) → τ r+1 (M, νF)
dénie par
L̃(ω)(X, Y1 , ..., Yr ) := (L̃X (ω))(Y1 , ..., Yr )
:= ∇X (ω(Y1 , ..., Yr )) −
r
X
ω(Y1 , ..., ∇M
X (Yi ), ..., Yr )
i=1
Proposition 27.
∀ω ∈ Ωr (M, νF),
on a
r+1
X
∇(ω)(Y1 , ..., Yr+1 ) =
(−1)i+1 (L̃Yi (ω))(Y1 , ..., Ŷi , ..., Yr+1 ).
i=1
33
Démonstration.
r+1
X
(−1)i+1 (L̃Yi (ω))(Y1 , ..., Ŷi , ..., Yr+1 )
i=1
r+1
X
=
(−1)i+1 ∇Yi (ω(Y1 , ..., Ŷi , ..., Yr+1 ))
i=1
+
r+1 X
r+1
X
(−1)i ω(Y1 , ..., Ŷi , ..., ∇M
Yi (Yk ), ..., Yr+1 )
i=1 k=1,k6=i
=
r+1
X
(−1)i+1 ∇Yi (ω(Y1 , ..., Ŷi , ..., Yr+1 ))
i=1
+
X
+
X
(−1)i ω(Y1 , ..., Ŷi , ..., ∇M
Yi (Yk ), ..., Yr+1 )
i<k
=
(−1)i ω(Y1 , ..., ∇M
Yi (Yk ), ..., Ŷi , ..., Yr+1 )
k<i
r+1
X
(−1)i+1 ∇Yi (ω(Y1 , ..., Ŷi , ..., Yr+1 ))
i=1
+
X
+
X
(−1)i ω(Y1 , ..., Ŷi , ..., ∇M
Yi (Yk ), ..., Yr+1 )
i<k
=
ˆ
(−1)k ω(Y1 , ..., ∇M
Yk (Yi ), ..., Yk , ..., Yr+1 )
i<k
r+1
X
(−1)i+1 ∇Yi (ω(Y1 , ..., Ŷi , ..., Yr+1 ))
i=1
+
X
+
X
(−1)i ω(Y1 , ..., Ŷi , ..., ∇M
Yi (Yk ), ..., Yr+1 )
i<k
(−1)k+k−i+1 ω(Y1 , ..., Yˆk , ..., ∇M
Yk (Yi ), ..., Yr+1 ).
i<k
Or la connexion de Levi-Civita est sans torsion,
donc
ω(Y1 , ..., Ŷi , ..., [Yi , Yk ], ..., Yr+1 ) = ω(Y1 , ..., Ŷi , ..., ∇M
Yi (Yk ), ..., Yr+1 )
− ω(Y1 , ..., Yˆk , ..., ∇M
Y (Yi ), ..., Yr+1 ).
k
34
Donc
r+1
X
(−1)i+1 (L̃Yi (ω))(Y1 , ..., Ŷi , ..., Yr+1 )
i=1
r+1
X
=
(−1)i+1 ∇Yi (ω(Y1 , ..., Ŷi , ..., Yr+1 ))
i=1
X
+
(−1)i ω([Yi , Yk ], Y1 , ..., Ŷi , ..., Yˆk , ..., Yr+1 )
i<k
= ∇(ω)(Y1 , ..., Yr+1 ).
Remarque.
En particulier pour
r=1
on a
∇(ω)(X, Y ) = ∇X (ω(Y )) − ∇Y (ω(X)) − ω([X, Y ])
= (L̃X (ω))(Y ) − (L̃Y (ω))(X).
Dénition 37.
α ∈ τ 2 (M, νF) le 2-tenseur déni par α = −L̃(π),
où la projection canonique π : T M → νF est vue comme un élément de
Ω1 (M, νF). Le tenseur α est appelé la deuxième forme fondamentale le long
Soit
des feuilles.
Remarque.
Si
X, Y ∈ Ξ(M ),
on a
α(X, Y ) = −∇X (π(Y )) + π(∇M
X (Y )).
Proposition 28.
La deuxième forme fondamentale
α
est symétrique.
Démonstration.
M
α(X, Y ) − α(Y, X) = −∇X (π(Y )) + π(∇M
X (Y )) + ∇Y (π(X)) − π(∇Y (X))
M
= −∇X (π(Y )) + ∇Y (π(X)) + π(∇M
X (Y ) − ∇Y (X))
= −∇X (π(Y )) + ∇Y (π(X)) + π([X, Y ])
= T∇ (X, Y ) = 0.
Remarque.
particulier
On note encore
∀U, V ∈ Γ(T F),
Proposition 29.
Si
α
on a
la restriction de
α(U, V ) =
Y ∈ Γ(T F ⊥ )
et
α
π(∇M
U (V
à
Γ(T F) × Γ(T F) ;
)).
∀U, V ∈ Γ(T F)
on a
M
LY (g)(U, V ) = g(∇M
U (Y ), V ) + g(U, ∇V (Y )).
35
en
Démonstration.
LY (g)(U, V )
= Y (g(U, V )) − g(LY (U ), V ) − g(U, LY (V ))
= Y (g(U, V )) − g([Y, U ], V ) − g(U, [Y, V ])
M
M
M
= Y (g(U, V )) − g(∇M
Y (U ) − ∇U (Y ), V ) − g(U, ∇Y (V ) − ∇V (Y ))
M
M
= (Y (g(U, V )) − g(∇M
Y (U ), V ) − g(U, ∇Y (V ))) + g(∇U (Y ), V )
+ g(U ∇M
V (Y ))
M
= g(∇M
U (Y ), V ) + g(U, ∇V (Y )).
Proposition 30.
∀Y ∈ Γ(T F ⊥ ), ∀U, V ∈ Γ(T F)
on a
LY (g|T F )(U, V ) = −2g(Y, α(U, V )).
Démonstration.
Comme la connexion de Levi-Civita est métrique on a
M
g(∇M
U (Y ), V ) = U (g(Y, V )) − g(Y, ∇U (V ))
= −g(Y, ∇M
U (V ))
= −g(Y, π(∇M
U (V )))
= −g(Y, α(U, V )).
g(U, ∇M
V (Y )) = −g(Y, α(U, V )).
LY (g|T F )(U, V ) = −2g(Y, α(U, V )).
De même on a
Donc
Proposition 31.
brés vectoriel
s ∈ Γ(νF), il existe
W (s) : T F → T F qui vérie
Pour tout
un unique morphisme de
∀U, V ∈ Γ(T F), gνF (α(U, V ), s) = g(W (s)(U ), V ).
De plus l'application
s 7→ W (s)
est
C ∞ (M )-linéaire.
On appellera cette application l'application de Weingarten.
Démonstration. ∀x ∈ M, gνF ,x (αx (Ux , .), sx ) est une forme linéaire sur Tx F ,
Tx F est un espace vectoriel de dimension nie,
∃!W (s)(U )x ∈ Tx F tel que gνF ,x (αx (Ux , .), sx ) = gx (W (s)(U )x , Vx ).
∞
L'application x 7→ gνF ,x (αx (Ux , .), sx ) est C ,
∞ et W (s)(U ) ∈ Γ(T F).
donc l'application x 7→ W (s)(U )x est C
De l'égalité gνF (α(U, V ), s) = g(W (s)(U ), V ) on deduit que l'application
s 7→ W (s) est C ∞ (M )-linéaire.
or
donc
Dénition 38.
L'application trW
: Γ(νF) → R
dénie par
une forme linéaire.
κ ∈ Ω1 (M ) dénie par
κ(s) = trW (s), ∀s ∈ Γ(νF).
On prolonge trW en une 1-forme
κ(V ) = 0, ∀V ∈ Γ(T F) et
La forme κ est appelée la 1-forme
de courbure principale.
36
s 7→ trW (s)
est
Remarque.
et
Soient
{e1 , ..., ep }
un repère orthonormé local de
TF
s ∈ Γ(νF).
p
X
trW (s) =
i=1
p
X
=
g(W (s)(ei ), ei )
g(π(∇M
ei (ei )), s)
i=1
= g(π(
p
X
∇M
ei (ei )), s).
i=1
Dénition 39.
Soit
{e1 , ..., ep }
un repère orthonormé local de
T F.
On appelle champ de vecteur de courbure principal le champ de vecteur
déni localement par
H = π(
p
X
H
∇M
ei (ei )).
i=1
En particulier la 1-forme duale de
H
est donc la 1-forme de courbure principal
du feuilletage.
3.2 Géométrie basique d'un feuilletage riemannien
Nous allons dénir la cohomologie basique du feuilletage
F.
Cette co-
homologie a pour but de représenter la cohomologie de l'espace des feuilles
M/F ,
bien que celui-ci ne soit pas muni d'une structure de variété en gé-
néral. Puisque nous nous plaçons dans le cadre des feuilletages riemanniens,
nous verrons plus tard que la cohomologie basique vérie les mêmes propriétés que la cohomologie de de Rham. Nous calculons explicitement cette
cohomologie dans le cas des feuilletages par suspension. Dans ce paragraphe
nous dénissons également la diérentielle transverse aux feuilles, la forme
volume transversale et l'opérateur de Hodge basique qui nous serons utiles
pour la suite.
3.2.1 Généralités
Dénition 40.
Soit
ω ∈ Ω∗ (M ),
on dit que
ω
est basique si
∀V ∈ Γ(T F), iV (ω) = LV (ω) = 0.
On note
Ω∗ (M/F)
rentielle graduée et
Remarque.
l'ensemble des formes basiques qui est une algèbre dié-
H ∗ (M/F)
Ω0 (M/F)
la cohomologie associée.
est l'ensemble des fonctions
des feuilles.
37
C∞
constantes le long
Proposition 32.
(x1 , ..., xp , y1 , ..., yq ) des coordonnées
ω ∈ Ω∗ (M ).
si et seulement si ω est de la forme
X
ω=
ωI dyi1 ∧ ... ∧ dyik
Soient
locales asso-
ciées à une carte feuilletée et
Alors
ω
est basique
16i1 <...<ik 6q
I = (i1 , ..., ik ) et ωi
∂
dire
(ωI ) = 0, ∀l.
∂xl
où
Démonstration.
Donc
est une fonction indépendante de
On suppose que
∀1 ≤ l ≤ p, i∂l (ω) = 0,
ω
donc
x1 , ..., xp ,
c'est-à-
est basique.
ω=
X
ωI dyi1 ∧ ... ∧ dyik .
i1 <...<ik
LX
V (ω) = 0, ∀V ∈ Γ(T F).
LV (ω) =
LV (ωI )dyi1 ∧ ... ∧ dyik +
De plus on a
Or
X
ωI LV (dyi1 ∧ ... ∧ dyik )
i1 <...<ik
i1 <...<ik
et
LV (dyi1 ∧ ... ∧ dyik ) = LV (dyi1 ) ∧ ... ∧ dyik + ... + dyi1 ∧ ... ∧ LV (dyik )
= dLV (yi1 ) ∧ ... ∧ dyik + ... + dyi1 ∧ ... ∧ dLV (yik )
= d(V (yi1 )) ∧ ... ∧ dyik + ... + dyi1 ∧ ... ∧ d(V (yik ))
= 0.
LV (ωI ) = 0, ∀V ∈ Γ(T F).
∂l (ωi ) = 0, ∀l.
X
suppose que ω =
ωI dyi1 ∧ ... ∧ dyik
Donc
En particulier
On
avec
i1 <...<ik
Soit
V ∈ Γ(T F),
donc
V =
p
X
∂
(ωi ) = 0, ∀l.
∂xl
V i ∂ xi .
i=1
X iV (ω) = 0. Or
LV (ωI )dyi1 ∧ ... ∧ dyik +
On a clairement
LV (ω) =
i1 <...<ik
X
ωI LV (dyi1 ∧ ... ∧ dyik ),
i1 <...<ik
LV (dyi1 ∧ ... ∧ dyik ) = 0.
∂
(ωI ) = 0, ∀l. Donc ω
LV (ωI ) = V (ωI ) = 0 car
∂xl
Comme précédemment
Donc
Proposition 33.
L'inclusion
Ω∗ (M/F) ,→ Ω∗ (M )
→ H 1 (M ).
est basique.
induit un morphisme
1
injectif d'espace vectoriel H (M/F)
Démonstration.
ω ∈ Ω1 (M/F) telle que ω = df où f ∈ C ∞ (M )
V ∈ Γ(T F). On a V (f ) = iV (df ) = iV (ω) = 0 car ω est basique.
0
1
Donc f ∈ Ω (M/F) et [ω] = 0 dans H (M/F).
Exemple 6.
M →B
où
Soient
On considère le feuilletage de codimension
M
et
B
sont des variétées compactes.
38
q
par bration
et
π:
π∗
Nous allons montrer que
est un isomorphisme de
Ω∗ (B)
sur
Ω∗ (M/F).
∗
∗
∗
Montrons d'abord que π (Ω (B)) ⊂ Ω (M/F).
∗
Soit V ∈ Γ(T F), iV (π (ω)) = iπ∗ (V ) (ω).
∗
Or ici T F = Ker π∗ , donc π∗ (V ) = 0 et iV (π (ω)) = 0.
∗
∗
∗
∗
De même iV (d(π (ω))) = 0. Donc π (Ω (B)) ⊂ Ω (M/F).
∗
On sait que π est une submersion, donc π est injective.
α ∈ Ω∗ (M/F), montrons qu'il existe ω ∈ Ω∗ (B) tel que α = π ∗ (ω).
Soient z ∈ M , U une carte en M et (x1 , ..., xp , y1 , ..., yq ) les coordonnées
locales sur U . Alors (y1 , ..., yq ) sont des coordonnées locales autour de π∗ (z).
Comme α est basique, localement α s'écrit sous la forme :
X
fI (y)dyi1 ∧ ... ∧ dyik où I = (i1 , ..., ik ).
αz =
Soit
i1 <...<ik
U
On pose ωπ(z)
=
X
fI (y)dyi1 ∧ ... ∧ dyik .
On a donc
α = π ∗ (ω U ).
i1 <...<ik
En prenant une partition de l'unité subordonnée à de telles cartes on obtient
ainsi une forme diérentielle
Donc
π∗
est surjective et
π∗
ω
sur
B
telle que
α = π ∗ (ω).
est un isomorphisme.
∗
De plus π induit un isomorphisme de
Dénition 41.
Soit X ∈ Ξ(M ),
∀V ∈ Γ(T F), [X, V ] ∈ Γ(T F).
H ∗ (B)
sur
H ∗ (M/F).
X est feuilleté si
Ξ(M, F) l'ensemble
on dit que
On note
des champs
feuilletés.
Proposition 34. L'ensemble des champs feuilletés Ξ(M, F) est un R-espace
vectoriel, une algèbre de Lie pour le crochet de Lie et un
De plus
Γ(T F)
est un idéal de
Ω0 (M/F)-module.
Ξ(M, F).
Démonstration. Soient X, Y ∈ Ξ(M, F) et V ∈ Γ(T F) alors
[[X, Y ], V ] = −[[V, X], Y ] − [[Y, V ], X] ∈ Γ(T F). Donc Ξ(M, F) est stable
par le crochet de Lie et donc une sous algèbre de Lie de Ξ(M ).
0
Soient X ∈ Ξ(M, F), f ∈ Ω (M/F) et V ∈ Γ(T F) alors
[f X, V ] = f [X, V ] − V (f )X = f [X, V ] car f ∈ Ω0 (M/F). Ainsi Ξ(M, F) est
stable par multiplication par les fonctions lisses basiques. Donc Ξ(M, F) est
0
un Ω (M/F)-module.
De plus Γ(T F) est clairement un idéal de Ξ(M, F) pour le crochet de Lie.
Dénition 42. On note Ξ(M/F) l'algèbre de Lie Ξ(M/F) = Ξ(M, F)/Γ(T F),
qui est appelée l'algèbre des champs de vecteurs basiques sur
L'algèbre de Lie
Ξ(M/F)
M.
0
est un Ω (M/F)-module.
Proposition 35. Soit X ∈ Ξ(M ), les assertions suivantes sont équivalentes :
(i) le champ de vecteurs
X (ϕX
t )t∈R
X
est un champ feuilletée,
∀t ∈ R,
(iii) dans une carte feuilleté (x1 , ..., xp , y1 , ..., yq ) les
selon y1 , ..., yq sont indépendantes de x1 , ..., xp .
(ii) le ot de
est feuilleté
39
composantes de
X
Démonstration. Le champ X est feuilleté si et seulement si
[X, Y ] = LX (Y ) ∈ Γ(T F), ∀Y ∈ Γ(T F).
Donc X est feuilleté si et seulement si le ot de X préserve
les feuilles.
Donc les deux premiers points sont équivalents.
(x1 , ..., xp , y1 , ..., yq ) des coordonnées locales adaptées au feuilletage F .
Soit f (x, y)∂yi un champ feuilleté,
alors [f (x, y)∂yi , ∂xk ] est tangent au feuilletage.
Or [f (x, y)∂yi , ∂xk ] = ∂xk (f (x, y))∂yi + f (x, y)[∂yi , ∂xk ] = ∂xk (f (x, y))∂yi .
Donc nécessairement ∂xk (f (x, y)) = 0 et f est indépendante de y .
Soit
Donc les champs feuilletés sont bien de la forme voulue.
Soit
X
un champ de vecteurs de la forme
fi (x, y)∂xi + gi (y)∂yi
et
h(x, y)∂xk
un champ tangent au feuilletage. On a
[f (x, y)∂xi + g(y)∂yi , h(x, y)∂xk ]
= [f (x, y)∂xi , h(x, y)∂xk ] + [g(y)∂yi , h(x, y)∂xk ]
= f (x, y)∂xi (h(x, y))∂xk − h(x, y)∂xk (f (x, y))∂xi + f (x, y)h(x, y)[∂xi , ∂xk ]
+ g(y)∂yi (h(x, y))∂xk − 0 + g(y)h(x, y)[∂yi , ∂xk ]
= f (x, y)∂xi (h(x, y))∂xk − h(x, y)∂xk (f (x, y))∂xi + f (x, y)h(x, y)[∂xi , ∂xk ]
+ g(y)∂yi (h(x, y))∂xk .
Comme
TF
est involutif, on a bien que
tangent au feuilletage. Donc
X
[f (x, y)∂xi + g(y)∂yi , h(x, y)∂xk ] est
est feuilleté.
Proposition 36. L'espace vectoriel des champs de vecteurs basiques Ξ(M/F)
est isomorphe aux sections de
Γ(T F)
dont les coordonnées locales dans une
carte feuilletée ne dépendent que des coordonnées transverses (on notera
ΓB (νF)
l'ensemble de ces sections).
Démonstration.
(x1 , ..., xp , y1 , ..., yq ) des
⊥
au feuilletage F . On identiera νF et T F .
Soit φ : Ξ(M/F) → ΓB (νF) dénie par
Soit
φ X=
p
X
i=1
q
coordonnées locales adaptées
X
∂
∂
fi (x, y)
+
gi (y)
∂xi
∂yi
!
i=1
φ est clairement un épimorphisme
Γ(T F). D'où le résultat.
L'application
noyau est
=
q
X
gi (y)
i=1
∂
.
∂yi
d'espace vectoriel, dont le
Le théorème suivant est démontré dans [Dom98].
Théorème 13.
Soit
F
un feuilletage riemmannien alors il existe une mé-
trique quasi-brée telle que la forme de coubure principale
Remarque.
Dans la suite on supposera donc que
κ
est basique.
κ est basique et par consé-
quent le champ de vecteur de courbure principal sera un champ de vecteur
basique.
40
Nous allons à présent dénir la diérentielle transverse aux feuilles (voir
par exemple [Mol88, Ton97]).
Dénition 43.
νF et T F ⊥ .
∗
∗
∗
On a T M = T F ⊕ νF , donc T M = T F ⊕ ν F .
Soit U une carte locale feuilletée de coordonnées (x1 , ..., xp , y1 , ..., yq ).
∗
Si ω ∈ Ω (M ) est de la forme
X
ω=
fi,j (x, y)dxi1 ∧ ... ∧ dxir ∧ dyj1 ∧ ... ∧ dyjs ,
On identie
i1 ,...,ir ,ji ,...,js
on dit que
On notera
ω est une forme de bidegré (r, s).
Ωr,s (M ) l'ensemble des formes de
Dénition 44.
bidegré
(r, s).
ω ∈ Ωr,s (M ), alors dω est la somme de formes de type
(r + 1, s), (r, s + 1), (r − 1, s + 2). On note dF ω la composante de bidegré
(r + 1, s) de dω , dt ω la composante de bidegré (r, s + 1) de dω , et d−1,2 ω
la composante de bidegré (r − 1, s + 2) de dω . L'application dF est appelée
diérentielle le long des feuilles et dt est appelée diérentielle transverse aux
Si
feuilles.
Proposition 37.
dF et d−1,2 vérient d2F = 0, d2−1,2 = 0,
dF d−1,2 + d−1,2 dF + dt = 0, d−1,2 dt + dt d−1,2 = 0 et dF dt + dt dF = 0.
Démonstration.
Or
Les applications
ω ∈ Ωr,s (M ), alors d2 ω ∈ Ωr+s+2 (M )
dω = (dF + d−1,2 + dt )ω . Donc
Soit
et
d2 ω = 0.
d2 ω = (d2F +dF d−1,2 + dF dt + d−1,2 dF
+ d2−1,2 + d−1,2 dt + dt dF + dt d−1,2 + d2t )ω = 0
d2F ω est l'unique composante de bidegré (r+2, s) dans d2 ω , donc d2F ω = 0.
2
Or (dF dt + dt dF )ω est la composante de bidegré (r + 1, s + 1) dans d ω ,
donc (dF dt + dt dF )ω = 0.
De la même manière on obtient dF d−1,2 + d−1,2 dF + dt = 0,
d−1,2 dt + dt d−1,2 = 0, et d2−1,2 = 0.
Or
Remarque.
Notons que dans ce paragraphe, nous n'avons pas utilisé le fait
que le feuilletage
F
est riemannien.
3.2.2 Cohomologie basique pour les suspensions
Notation 8.
ρ : π1 (B) → Isom(T )
un morphisme de groupe. On note Γ = ρ(π1 (B)), M̃ = B̃ × T et M = M̃ /Γ
munie du feuilletage dénie par la suspension du groupe Γ et du morphisme
ρ (voir proposition 116 page 118).
On va calculer la cohomologie basique de (M, F).
Soient
T
et
B
des variétés compactes et
41
Lemme 2.
On note
π : M̃ → M
la projection canonique.
Ẽ = π ∗ (E), alors l'application π induit un
isomorphisme de Γ(M, E) sur Γ(M̃ , Ẽ/Γ), où Γ(M̃ , Ẽ/Γ) désigne l'ensemble
des sections Γ-invariantes de Ẽ .
Soit
E→M
un bré vectoriel et
En particulier on a
C ∞ (M ) ∼
= C ∞ (M̃ /Γ), Ξ(M ) ∼
= Ξ(M̃ /Γ)
Démonstration.
et
Ω∗ (M ) ∼
= Ω∗ (M̃ /Γ).
M = M̃ /Γ, la projection π est
C ∞ (M ) ∼
= C ∞ (M̃ /Γ).
Soit U une carte locale de M trivialisant le bré E .
Donc Γ(E|U ) ∼
= C ∞ (U )N où N est le rang du bré E
et Γ(Ẽ|π −1 (U ) ) ∼
= C ∞ (π −1 (U ))N ∼
= (C ∞ (U/Γ))N ∼
= (C ∞ (U )N )Γ où (C ∞ (U )N )Γ
∞
N
désigne l'ensemble des éléments de (C (U ) ) invariants par l'action de Γ.
Par dénition du quotient
un revêtement et on a un isomorphisme
D'où le résultat.
Lemme 3.
ω ∈ Ω∗ (T /Γ), alors il existe une unique forme diérentielle
φ(ω) ∈ Ω∗ (M ) telle que π ∗ (φ(ω)) = q2∗ (ω), où q2 : M̃ → T désigne la
Soit
deuxième projection.
Démonstration.
∗
Or π
:
Ω∗ (M )
q2 est Γ-équivariante, q2∗ (ω) est Γ-invariante.
∗
Ω (M̃ /Γ) est un isomorphisme, donc il existe une unique
Puisque
→
forme diérentielle
φ(ω) ∈ Ω∗ (M )
Proposition 38.
L'application
ment vérie :
De plus
φ
telle que
π ∗ (φ(ω)) = q2∗ (ω).
φ : Ω∗ (T /Γ) → Ω∗ (M )
φ(Ω∗ (T /Γ)) ⊂ Ω∗ (M/F).
dénie précédem-
est un isomorphisme d'algèbre diérentielle graduée de
∗
sur Ω (M/F) et
φ
∗
induit un isomorphisme de H (T /Γ) sur
Ω∗ (T /Γ)
H ∗ (M/F).
Démonstration.
Soit V ∈ Γ(T F), il existe un unique champ de vecteurs
Ṽ ∈ Γ(T F̃) tel que V = π∗ (Ṽ ). Montrons que iV (φ(ω)) = 0.
∗
∗
∗
On a π (iV (φ(ω))) = iṼ (π (φ(ω)) = iṼ (q2 (ω)) = 0 car q2,∗ (Ṽ ) = 0.
∗
∗
∗
Or π : Ω (M ) → Ω (M̃ /Γ) est un isomorphisme, donc iV (φ(ω)) = 0.
Montrons que dM φ(ω) = φ(dT ω) où dM désigne la diérentielle de de Rham
sur M et dT désigne la diérentielle de de Rham sur T .
π ∗ (dM φ(ω)) = dM̃ (π ∗ (φ(ω)))
= dM̃ (q2∗ (ω))
= q2∗ (dT ω)
= π ∗ (φ(dT ω))
dM φ(ω) = φ(dT ω). Par conséquent on obtient de la même manière que
précédemment iV (d(φ(ω)) = 0. Ainsi φ(ω) est basique.
De plus φ est clairement un homomorphisme d'algèbres graduées.
Donc
42
Montrons que
φ
est injective.
φ(ω) = 0 ⇒ π ∗ (ω) = 0
⇒ q2∗ (ω) = 0
⇒ω=0
φ est injective.
φ est surjective.
∗
∗
Soit ω ∈ Ω (M/F), on a π (ω) est F̃ -basique et Γ-invariante,
∗
∗
Γ
∗
Γ
donc π (ω) ∈ Ω (M̃ /F̃) où Ω (M̃ /F̃) désigne les formes diérentielles
F̃ -basique et Γ-invariante.
∗
∗
Γ
∗
Γ
Montrons que q2 : Ω (T ) → Ω (M̃ /F̃) est un isomorphisme.
∗
∗
∗
Or M̃ → T est une bration (non-compacte), donc q2 : Ω (T ) → Ω (M̃ /F̃)
car
q2
est une bration. Donc
Montrons que
est un isomorphisme.
q2 est Γ-équivariante, donc q2∗ induit un isomorphisme
: Ω∗ (T )Γ → Ω∗ (M̃ /F̃)Γ .
∗
∗
∗
Donc il existe α ∈ Ω (T /Γ) tel que q2 (α) = π (ω), et φ est
Or
q2∗
surjective.
Proposition 39. On note G l'adhérence de Γ dans le groupe de Lie compact
Isom(T ) des
H ∗ (T /G).
isométries de
Démonstration.
T.
Alors
Ω∗ (M/F) = Ω∗ (T /G)
On rappelle que le groupe
G
et
H ∗ (M/F) =
est muni de la topologie com-
pact ouvert engendrée par les ensembles de la forme
W (K, U ) = {g ∈ Isom(M )/g(K) ⊂ U }
où
K
est un compact de
M
et
U
un ouvert de
M
(voir [Hel01]). Cette
topologie est la topologie initiale associée à la famille de semi-normes
pK,j (g) = supx∈K ||Dj g(x)||.
(gk )k une suite de Γ convergeant vers g ∈ G et ω ∈ Ω∗ (T /Γ).
∗
∗
Donc gk (ω) = ω, ∀k et en passant à la limite on a g (ω) = ω .
∗
∗
∗
∗
∗
Donc Ω (T /Γ) ⊂ Ω (T /G) et Ω (T /G) = Ω (T /Γ) = Ω (M/F).
Soit
Exemple 7.
Reprenons l'exemple du feuilletage de Kronecker
T = S1,
Γ = Z, M = S 1 × S 1 /Z. La cohomologie basique est alors donnée par
H ∗ (S 1 /Γ) où Γ est l'image du morphisme ρ : Z → Isom(S 1 ).
1
0
1
Rappelons que la cohomologie du cercle S est donnée par H (S ) ∼
= R et
1
1
∼
H (S ) = R.
0
1
L'espace H (S ) est représenté par les fonctions constantes,
0
1
donc H (S /Γ) ∼
= {0} et par dualité de Poincaré on obtient H 1 (S 1 /Γ) ∼
= {0}.
43
3.2.3 Forme volume transversale et opérateur de Hodge basique
Supposons à présent que le feuilletage
F
est également transversalement
orientable.
Dénition 45.
Soit
(F1 , ..., Fq )
un repère orthonomé de
ν∈
On appelle forme volume transversale la forme
νF .
Ωq (νF) dénie par
ν(s1 , ..., sq ) = det(g(si , Fj ))i,j , ∀si ∈ Γ(νF).
Proposition 40.
Démonstration.
La forme volume transversale
ν
vérie
LV (ν) = 0, ∀V ∈ Γ(T F).
P
det(g(si , Fj )) =
σ∈Sq (σ)g(s1 , Fσ(1) )...g(sq , Fσ(q) ).
On a
Par conséquent
LV (ν)(s1 , ..., sq ) =
X
(σ)LV (g(s1 , Fσ(1) )...g(sq , Fσ(q) ))
σ∈Sq
=
X
(σ)g(s1 , Fσ(1) )...LV (g)(si , Fσ(i) )...g(sq , Fσ(q) ).
σ∈Sq
Comme la métrique
Remarque.
en une
est quasi-brée, on obtient le résultat voulu.
On considère
q -forme ν ∈
Proposition 41.
Démonstration.
On note
g
Xi =
ν
T F ⊥ , donc ν
= 0, ∀V ∈ Γ(T F).
comme un élément de
Ωq (M ) qui vérie iV (ν)
La forme volume transversale
X1 , ..., Xq ∈ Ξ(M ).
00
Xi , où Xi0 ∈ Γ(T F) et Xi00
q
X
ν
se prolonge
est une forme basique.
Soient
Xi0
+
LV (ν)(X1 , ..., Xq ) = V (ν(X1 , ..., Xq )) −
∈ Γ(T F ⊥ ).
ν(X1 , ..., LV (Xi ), ..., Xq ).
i=1
Comme
iV (ν) = 0, ∀V ∈ Γ(T F),
par multilinéarité on a
LV (ν)(X1 , ..., Xq ) = V (ν(X100 , ..., Xq00 )) −
q
X
ν(X1 , ..., LV (Xi0 ), ..., Xq )
i=1
−
q
X
ν(X100 , ..., LV (Xi00 ), ..., Xq00 )
i=1
=V
(ν(X100 , ..., Xq00 ))
−
q
X
ν(X1 , ..., [V, Xi0 ], ..., Xq )
i=1
−
q
X
ν(X100 , ..., LV (Xi00 ), ..., Xq00 ).
i=1
44
Puisque
et
TF
est involutif,
LV (ν)(X1 , ..., Xq ) = V
[V, Xi0 ] ∈ Γ(T F),
(ν(X100 , ..., Xq00 ))
−
q
X
ν(X100 , ..., LV (Xi00 ), ..., Xq00 ).
i=1
LV (ν)(X1 , ..., Xq ) = LV (X100 , ..., Xq00 )
précédente entraîne que LV (ν) = 0.
On a alors
position
Proposition 42.
La forme
ν
Xi00 ∈ Γ(T F ⊥ ).
où
est une forme fermée, c'est-à-dire
La pro-
dν = 0.
Démonstration.
On a ∀V ∈ Γ(T F), LV (ν) = 0,
(iV ◦ d + d ◦ iV )(ν) = 0. Or iV (ν) = 0,
q+1 (νF), et dν = 0.
conséquent dν ∈ Ω
c'est-à-dire
Par
Comme
M
est une variété orientable et
F
donc
est transversalement orientable,
le bré vectoriel
TF
Dénition 46.
On appelle forme caractéristique de
long des feuilles) la
iV ◦ d(ν) = 0.
est orientable.
p-forme
sur
M
dénie par
F (ou forme volume le
χF = ∗ν où ∗ est l'opérateur
de Hodge.
Quitte à changer l'orientation de
tation de
T F , on peut supposer que χF
dénit l'orien-
T F.
Par conséquent si
(E1 , ..., Ep ) est un repère orthonormé de T F , χF ∈ Ωp (M )
est donnée par
χF (Y1 , ..., Yp ) = det(g(Yi , Ej ))i,j , ∀Yi ∈ Ξ(M ).
Remarque.
On a
χF ∧ ν = dvol la forme volume
⊥
(ii) ∀Y ∈ Γ(T F ), iY (χF ) = 0.
(i)
canonique de
Proposition 43 (formule de Rummler [Rum79]).
χF
M,
La forme caractéristique
vérie
dχF = −κ ∧ χF + ϕ0
où
ϕ0 ∈ Ωp+1 (M )
vérie
∀V1 , ..., Vp ∈ Γ(T F), iV1 ◦ ... ◦ iVp (ϕ0 ) = 0
et
κ
est
la forme de courbure principale.
Démonstration.
Calculons
LY (χF )(E1 , ..., Ep )
45
où
Y ∈ Γ(T F)
et
Ek
est un
repère orthonormé (local) de
T F.
LY (χF )(E1 , ..., Ep ) = Y (χF (E1 , ..., Ep )) −
p
X
χF (E1 , ..., LY (Ek ), ..., Ep )
k=1
p
X
= Y (1) −
g(LY (Ek ), Ek )χF (E1 , ..., Ep )
k=1
=−
p
X
g([Y, Ek ], Ek )
k=1
=
p
X
g([Ek , Y ], Ek ).
k=1
Or la connexion de Levi-Civta
∇M
est une connexion métrique,
g(∇M
Y (Ek ), Ek )
− g(Ek , ∇M
Y (g(Ek , Ek )) −
Y (Ek )) = 0,
M
M
donc Y (1) − 2g(∇Y (Ek ), Ek ) = 0 et g(∇Y (Ek ), Ek ) = 0.
p
X
Donc LY (χF )(E1 , ..., Ep ) =
g(∇M
Y (Ek ) + [Ek , Y ], Ek ).
donc
k=1
Or
∇M
Donc
est sans torsion, donc
LY (χF )(E1 , ..., Ep ) =
M
∇M
Y (Ek ) + [Ek , Y ] = ∇Ek (Y ).
p
X
g(∇M
Ek (Y ), Ek ).
k=1
Y ∈ Γ(T F ⊥ ).
p
X
κ(Y ) = trW (Y ) =
g(W (Y )(Ek ), Ek ),
Calculons
On a
κ(Y )
où
où
W
est l'application de
k=1
Weingarten introduite à la proposition 36. Donc
κ(Y ) =
p
X
g(∇M
Ek (Ek ), Y ).
k=1
Comme
on a
∇M
κ(Y ) =
est une connexion métrique,
p
X
Ek (g(Ek , Y )) − g(Ek , ∇M
Ek (Y )).
k=1
Or
et
Y ∈ Γ(T F ⊥ ) et Ek est repère
p
X
κ(Y ) =
−g(Ek , ∇M
Ek (Y )).
de
T F,
donc
g(Ek , Y ) = 0,
k=1
LY (χF )(E1 , ..., Ep ) = −κ(Y )χF (E1 , ..., Ep ).
p
Donc LY (χF ) = −κ(Y )χF + ω où ω ∈ Ω (M ) vérie la condition voulue.
C'est-à-dire (iY ◦ d + d ◦ iY )(χF ) = −iY (κ ∧ χF ) + ω puisque χF est nulle
sur T F .
Donc iY dχF = −iY (κ ∧ χF ) + ω ,
p+1 (M ) vérie la condition voulue.
et dχF = −κ ∧ χF + ϕ0 où ϕ0 ∈ Ω
Donc
Proposition 44.
Si
α ∈ Ωq−1 (M/F),
46
la
p + 1-forme ϕ0
vérie
α ∧ ϕ0 = 0.
De plus si la forme de courbure principale
Démonstration.
Soient
κ est nulle on a alors α ∧ dχF = 0.
(x1 , ..., xp , y1 , ..., yq )
les coordonnées associées à une
carte feuilletée.
X1 , ..., Xn les champs de vecteurs dénis par Xi = ∂xi , ∀ ≤ i ≤ p
et Xi = ∂yj , ∀1 ≤ j ≤ q .
P
(ϕ0 ∧ α)(X1 , ..., Xn ) = σ∈Sn ϕ0 (Xσ(1) , ..., Xσ(p+1) )α(Xσ(p+2) , ..., Xσ(n) )
or α est basique, donc ∀V ∈ Γ(T F), iV (α) = 0.
Donc α(Xσ(p+2) , ..., Xσ(n) ) 6= 0 seulement si ∀p + 2 ≤ i ≤ n, Xσ(i) ∈
/ Γ(T F),
et dans ce cas ∀1 ≤ i ≤ p, ∂xi ∈ {Xσ(1) , ..., Xσ(p+1) },
donc ϕ0 (Xσ(1) , ..., Xσ(p+1) ) = 0,
donc ϕ0 ∧ α(X1 , ..., Xn ) = 0.
On note
Dénition 47. On appelle opérateur de Hodge basique l'application linéaire
¯∗ : Ωk (M/F) → Ωq−k (M/F)
Lemme 4.
ω ∈ Ω∗ (M/F)
Soit
Démonstration.
dénie par
Soient
alors
¯∗ω
¯∗ω = (−1)p(q−k) ∗ (ω ∧ χF ).
est une forme basique.
(x1 , ..., xp , y1 , ..., yq ) des coordonnées locales associées
à une carte feuilletée.
On peut écrire
ω
sous la forme
¯
∗ω = (−1)p(q−k)
X
ω=
P
i ωi dyi1
∧ ... ∧ dyik
donc
ωi ∗ (dyi1 ∧ ... ∧ dyik ∧ χF )
i
= (−1)p(q−k)
X
ωi ∗ (dyi1 ∧ ... ∧ dyik ∧ dx1 ∧ ... ∧ dxp )
i
X
=
ωi dyj1 ∧ ... ∧ dyjq−k
i
où
=1
ou
−1.
Donc
Proposition 45.
¯
∗ω
est une forme basique.
∀ω ∈ Ωk (M/F), ∗ω = ∗¯ω ∧ χF
(ii) ∀α, β ∈
α ∧ ¯∗β = (−1)pq hα, βig ν
k
(iii) ∀α, β ∈ Ω (M/F), α ∧ ¯
∗β = β ∧ ¯∗α
k
(iv) ∀ω ∈ Ω (M/F), ¯
∗2 ω = (−1)k(q−k) ω
(i)
Ωk (M/F),
Démonstration.
Soient
(x1 , ..., xp , y1 , ..., yq ) des coordonnées locales associées
à une carte feuilletée.
P
ω sous
P la forme ω = i ωi dyi1 ∧ ... ∧ dyik ,
donc ∗ω = i ωi dx1 ∧ ... ∧ dxp ∧ dyj1 ∧ ... ∧ dyjq−k où {j1 , ..., jq−k }
est le complémentaire de {1, ..., k} dans {1, ..., q} et est la signature
1
...
n
de la permutation
.
i1 ... ik 1 ... p j1 ... jq−k
(i) On écrit
47
Donc
∗ω = (−1)p(q−k)
P
i ωi dyj1
∧ ... ∧ dyjq−k ∧ dx1 ∧ ... ∧ dxp .
De plus on a
X
¯
∗ω = (−1)p(q−k) ∗ (
ωi dyi1 ∧ ... ∧ dyik ∧ dx1 ∧ ... ∧ dxp )
i
p(q−k)+pk
= (−1)
X
∗(
ωi dx1 ∧ ... ∧ dxp ∧ dyi1 ∧ ... ∧ dyik )
i
pq 0
= (−1) X
ωi dyj1 ∧ ... ∧ dyjq−k
i
0
est la signature de la permutation
1
...
n
.
1 ... p i1 ... ik j1 ... jq−k
0
pk
Or = (−1) .
où
Donc
¯
∗ω ∧ χF = (−1)p(q+k) X
ωi dyj1 ∧ ... ∧ dyjq−k ∧ dx1 ∧ ... ∧ dxp
i
= (−1)p(q−k) X
ωi dyj1 ∧ ... ∧ dyjq−k ∧ dx1 ∧ ... ∧ dxp
i
= ∗ω.
α = dyi1 ∧ ... ∧ dyik
β = dyl1 ∧ ... ∧ dylk .
Donc ¯
∗β = (−1)pq dyj1 ∧ ... ∧ dyjq−k où est la signature de la permu
1
...
n
tation
.
1 ... p l1 ... lk j1 ... jq−k
Donc α ∧ ¯
∗β = (−1)pq dyi1 ∧ ... ∧ dyik ∧ dyj1 ∧ ... ∧ dyjq−k .
S'il existe des indices tel que dyim = dyjn , alors α ∧ ¯
∗β = 0 ;
pq
0
¯
sinon α ∧ ∗β = (−1) ν , où
1
...
q
0
est la signature de la permutation
.
i1 ... ik j1 ... jq−k
Or hα, βig = 1 si et seulement si les mêmes dyim apparaissent dans
0
l'écriture de α et β et dans ce cas = ,
c'est-à-dire si et seulement si α et ¯
∗β n'ont aucun dyim en commun.
pq
Donc on a bien α ∧ ¯
∗β = (−1) hα, βig ν .
k
(iii) Soient α, β ∈ Ω (M/F),
(ii) Sans perte de généralité, on peut supposer que
et
α ∧ ¯∗β = (1)pq hα, βig ν
= (−1)pq hβ, αig ν
= β ∧ ¯∗α.
ω ∈ Ωk (M/F).
P
écrit ω sous la forme ω =
i ωi dyi1 ∧ ... ∧ dyik ,
(iv) Soit
On
48
on a
X
¯
∗ω = (−1)p(q−k) ∗ (
ωi dyi1 ∧ ... ∧ dyik ∧ dx1 ∧ ... ∧ dxp )
i
p(q−k)+pk
= (−1)
X
∗(
ωi dx1 ∧ ... ∧ dxp ∧ dyi1 ∧ ... ∧ dyik )
i
pq
= (−1) X
ωi dyj1 ∧ ... ∧ dyjq−k
i
où
{j1 , ..., jq−k }
{1, ..., k} dans {1, ..., q} et 1
...
n
.
1 ... p i1 ... ik j1 ... jq−k
est le complémentaire de
est la signature de la permutation
¯
∗2 ω
= (−1)p(q−(q−k)) (−1)pq ∗ (
X
ωi dyj1 ∧ ... ∧ dyjq−k ∧ dx1 ∧ ... ∧ dxp )
i
= (−1)p(k+q) (−1)p(q−k) ∗ (
X
ωi dx1 ∧ ... ∧ dxp ∧ dyj1 ∧ ... ∧ dyjq−k )
i
0
= X
ωi dyi1 ∧ ... ∧ dyik
i
0
est la signature de la permutation
1
...
n
.
1 ... p j1 ... jq−k i1 ... ik
0
k(q−k) .
Or = (−1)
2
Donc ¯
∗ ω = (−1)k(q−k) ω .
où
Remarque.
Ω∗ (M/F)
On peut réécrire le produit scalaire sur
2
produit scalaire L sur
forme caractéristique
k
M
χF :
induit par le
à l'aide de l'opérateur de Hodge basique et de la
Z
∀α, β ∈ Ω (M/F), hα, βiM =
49
Z
α ∧ ∗β =
M
α ∧ ¯∗β ∧ χF .
M
Chapitre 4
Opérateurs diérentiels
basiques
Dans ce paragraphe nous reprenons en détails l'article d'Aziz El KacimiAlaoui Opérateurs transversalement elliptiques sur un feuilletage riemannien et applications [EKA90], en complétant certains résultats, an de montrer qu'un opérateur diérentiel basique transversalement elliptique se comporte comme un opérateur diérentiel elliptique. Nous étudions ensuite le
cas particulier du Laplacien basique, de l'opérateur de de Rham basique,
de l'opérateur de signature basique, de l'opérateur de Dolbeault basique, et
l'opérateur de Dirac basique. De plus nous interprétons l'indice de ces opérateurs en termes d'invariants géométriques liés au feuilletage et calculons
des exemples.
4.1 Opérateurs transversalement elliptiques
Commençons par rappeler la notion d'espace de Sobolev basique ([KT87]).
On désigne toujours par
Dénition 48.
norme
||ω||2B,s =
Soit
s
X
∇
la connexion de Levi-Civita transverse.
s ∈ N
on appelle
||∇k (ω)||2B ,
où
s-norme
de Sobolev sur
Λν ∗ F
∇k (ω) ∈ Γ(hom(νF ⊗k , νF)/F)
et
la
||.||B
k=0
est la norme induite par la norme
Dénition 49.
On appelle
L2 .
s-ième espace de Sobolev basique la complétion
||.||B,s . On notera cet espace H s (M/F).
∗
de Λν F par rapport à la norme
Remarque.
La norme
Remarque.
Comme la connexion
||.||B,s
ne dépend que de la métrique transverse
∇
gνF .
est donnée dans les directions trans-
verses par la projection de la connexion de Levi-Civita, on obtient le dia-
50
gramme commutatif suivant :
- H s (Λν ∗ F)
H s (M/F)
6
6
Ω∗ (M/F)
H s (M/F) est isométrique à l'adhérence de Λν ∗ F
En particulier
Remarque.
On note
||.||s
- Γ(Λν ∗ F)
On identie
Λν ∗ F
avec un sous-bré de
dans
H s (Λν ∗ F)).
ΛT ∗ M .
H s (Ω∗ (M )).
H s (Ω∗ (M )) = H s (ΛT ∗ M )
la norme de Sobolev sur
On sait que la norme de Sobolev sur
induit une
s
∗
s
∗
norme sur H (Λν F) ⊂ H (Ω (M )).
s
s
∗
Donc H (M/F) ⊂ H (Ω (M )) est topologiquement équivalent à l'adhérence
∗
s
∗
de Ω (M/F) dans H (Ω (M )) muni de la norme ||.||s , c'est-à-dire que les
normes
||.||B,s
et
||.||s
sont équivalentes.
On a donc le diagramme commutatif suivant :
H s (M/F)
- H s (Ω∗ (M ))
6
6
Ω∗ (M/F)
- Ω∗ (M )
Théorème 14 (lemme de Rellich basique).
s+t (M/F)
inclusions H
Démonstration.
Théorème 15
,→
s∈N
et
t ∈ N∗ ,
alors les
H s (M/F) sont compactes et denses.
Voir [KT87].
(d'inclusion de Sobolev basique)
s
inclusion continue H (M/F)
Démonstration.
Soient
⊂
C k (M/F).
.
Soit
s>
n
+ k,
2
on a une
Voir [KT87].
Remarque. Si E est un F -bré vectoriel (voir annexe B) et ∇ une connexion
E , on dénit de la même manière les espaces de Sobolev basiques
H s (M, E/F) (notés aussi H s (E/F) s'il n'y a pas d'ambiguïté) qui vérient
s
les mêmes propriétés que H (M/F).
basique sur
Dénition 50.
E et E 0 des F -brés vectoriel de rang N et N 0 .
0
On dit que D : Γ(E/F) → Γ(E /F) est un opérateur diérentiel basique
d'ordre m ∈ N, si D est une application linéaire et sur une carte feuilletée
de coordonnées (x1 , ..., xp , y1 , ..., yq ), D s'écrit
X
D=
as (y)Dα
Soient
|s|≤m
51
où
Dα = i|α|
∂s
q
s , s∈N
∂y1s1 ...∂yq q
Remarque.
as (y)
0
as (y) ∈ hom(E(x,y) , E(x,y)
).
et
En utilisant des trivilisations locales de
comme un élément de
MN,N
E
et
E0
on peut voir
∞ (M/F)).
0 (C
Dénition 51. Le bré conormal ν ∗ F s'identie avec {ξ ∈ T ∗ M/ξ(X) = 0}.
z ∈ M un point de coordonnées (x, y) et ξ ∈ ν ∗ F , le symbole principal
D en z et ξ est l'application linéaire σ(D)(z, ξ) : Ez → Ez0 dénie par
X
s
ξ1s1 ...ξq q as (y).
σ(D)(x, ξ) = im
Soient
de
|s|=m
On dit que
D
est
F -transversalement
elliptique (ou transversalement ellip-
tique s'il n'y a pas d'ambiguïté)si pour tout
ξ∈
z ∈ M,
et pour tout
νF ∗ ,
σ(D)(x, ξ) est un isomorphisme.
D est fortement transversalement elliptique si pour
∗
tout ξ ∈ ν F non-nul, σ(D)(x, ξ) est dénie positive.
On dit que
et pour
tout
z ∈ M,
Remarque. On note π : T ∗ M → M la projection. Alors le symbole principal
de
D
est une section basique du bré
Exemple 8.
Ω∗ (M/F),
Alors
dB
hom(π ∗ (E), π ∗ (E 0 )).
dB la restriction de la diérentielle de de Rham
∗
Ω (M/F) → Ω∗ (M/F).
On note
dB :
d
à
est un opérateur diérentiel basique d'ordre 1.
De plus son symbole est donné par
Remarque.
σ(dB )(z, ξ)(ω) = iξ ∧ ω
où
ω ∈ Λν ∗ Fz .
An de montrer qu'un opérateur transversalement elliptique
se comporte comme un opérateur elliptique usuel, nous allons procéder en
trois étapes en suivant le théorème de Molino : le cas des feuilletages de Lie à
feuilles denses, le cas des feuilletages transversalement parallélisables et enn
le cas des feuilletages riemanniens. Nous commençons par traiter le cas des
feuilletages à feuilles denses dont se déduisent les autres cas. Dans la suite
D : Γ(E/F) → Γ(E 0 /F) un
0
opérateur diérentiel basique transversalement elliptique d'ordre m = 2m
0
0
(si D est un opérateur d'odre m on se ramène à un opérateur d'ordre 2m
∗
en remplaçant D par D D ).
E
et
E0
désignent des
Proposition 46.
denses. Alors
nie,
D
F -brés
hermitiens et
On suppose que
Γ(E/F)
et
Γ(E 0 /F)
F
est un feuilletage de Lie à feuilles
sont des espaces vectoriels de dimension
est un opérateur de Fredholm et
ind(D)
= dim Γ(E/F) − dim Γ(E 0 /F).
52
Démonstration. Soient z ∈ M, evz : Γ(E/F) → Ez , σ 7→ σz et
σ ∈ Γ(E/F) tel que σz = 0.
Si γ est un chemin le long d'une feuille de F tel que γ(t0 ) = z , alors
γ̇ ∈ Γ(T F) et comme σ est basique ∇γ̇ (σ) = 0. C'est-à-dire σ est parallèle le long de γ .
Comme σz est nul, σ est nulle le long de γ .
Par connexité des feuilles σ est nulle le long de la feuille en z .
Or le feuilletage F est un feuilletage à feuilles denses, donc σ est nulle sur
M . Ainsi evz est injective et dim Γ(E/F) ≤ rang(E) < ∞.
0
0
De même dim Γ(E /F) ≤ rang(E ).
Par conséquent D est une application linéaire agissant sur des espaces vecoriels de dimension nie, et D est Fredholm et ind(D) = dim Γ(E/F) −
dim Γ(E 0 /F).
Remarque.
Notons que nous avons uniquement utilisé le fait que le feuille-
tage était à feuilles denses.
Remarque.
Nous allons à présent supposer que
(M, F)
est un feuilletage
transversalement parallélisable.
On sait alors par le théorème de Molino que les adhérences des feuilles sont les
bres d'une bration localement triviale
∞
De plus on a C (M/F)
Dénition 52.
On note
Lu
π : M → W . On notera k = dim W .
u ∈ W , on considére le F -bré hermitien E .
de π en u (Lu est l'adhérence d'une feuille de F
Soit
la bre
u).
feuilletage F
∼
= C ∞ (W ).
qui se
projette sur
Le
induit un feuilletage sur
Lu
qui est un feuilletage de Lie à
feuilles denses.
dim Γ(Lu , E/F) < +∞
Γ(Lu , E/F).
Donc
Proposition 47.
Avec les notations précédentes,
hermitien au-dessus de
Démonstration.
dante de
u.
(voir proposition 46 page 52) et on pose
W
Ē
est un bré vectoriel
appelé bré utile.
Montrons tout d'abord que la dimension de
Soient
u1
et
Ēu =
u2
des points de
Les automorphismes innitésimaux de
F
Ēu
est indépen-
W.
se relèvent naturellement (puisque
F -bré) en automorphismes innitésimaux de FE (le feuilletage inF sur le bré E ), et il en est de même du groupe qu'ils engendrent.
Or ce groupe est transitif sur M et se projette sur W .
Donc il existe dans ce groupe un élément γ tel que γ(Lu1 ) = Lu2 .
E
est un
duit par
53
Si
γE
est son relevé, le diagramme suivant est commutatif :
γE
- Eu
2
Eu1
?
γ
Lu1
L'automorphisme
Par dénition
dimension
N0
On dénit sur
Ē
γE
?
- Lu
2
induit alors un isomorphisme entre
est la réunion pour chaque
u ∈ W,
Ēu1
et
Ēu2 .
d'un espace vectoriel de
associé à ce point.
Ē
une structure de bré vectoriel au-dessus de
W
à l'aide des
trivialisations locales suivantes :
u0 ∈ W, z0 ∈ π −1 (u0 ) et N0 sections basiques α1 , ..., αN0 de E linéairement indépendantes en z0 .
L'ouvert de M où ces sections restent linéairement indépendantes est saturé pour la bration π , donc se projette sur un ouvert U de W dans lequel
α1 , ..., αN0 dénissent une trivialisation locale de Ē .
soient
Il est immédiat de vérier que ces trivialisations locales sont diérentiablement compatibles (le passage d'une telle trivialisation à une autre se faisant
par une matrice de fonctions basiques, regardées comme fonctions diérentiables sur
On note
h
W ).
la métrique hermitienne sur
u ∈ W , l'espace
métrique h.
Comme pour tout
provenant de la
Le bré
Ē
E.
vectoriel
Ēu
est muni d'une métrique
est alors canoniquement munie d'une métrique hermitienne
h̄u
h̄.
Proposition 48.
Soit ψ : Γ(E/F) → Γ(Ē), σ 7→ ψ(σ)
ψ(σ)u = σ|Lu ∈ Ēu .
L'application ψ est un isomorphisme.
−1 (s) = s
De plus ∀s ∈ Γ(Ē), ψ
z
π(z) (z) ∈ Ez , ∀z ∈ M .
où
Démonstration.
Par dénition de
ψ −1 ,
il est trivial que si
s ∈ Γ(Ē)
alors
ψ −1 (s) est basique.
Un simple calcul montre que
Dénition 53.
ψ −1
est bien l'inverse de
ψ.
M induit une métrique riemandµ la mesure sur W induite par cette métrique.
Comme la métrique h sur E est invariante le long des feuilles,
si α, β ∈ Γ(E/F), la fonction z ∈ M 7→ hz (αz , βz ) ∈ C est basique et induit
donc une fonction sur W notée θ(α, β).
On dénit alors un produit scalaire sur Γ(E/F) par
Z
hα, βiE =
θ(α, β)(w)dµ(w).
nienne sur
W.
La métrique quasi-brée sur
On notera
W
54
Proposition 49.
h̄,
Démonstration.
et
Γ(Ē) du produit scalaire induit par la métrique
ψ : Γ(E/F) → Γ(Ē) est une isométrie.
Z
dénition hψ(α), ψ(β)iĒ =
h̄(ψ(α), ψ(β))dµ.
On munit
alors l'application
Par
W
h̄(ψ(α), ψ(β)) = h(α,Zβ).
Donc
hψ(α), ψ(β)iĒ =
Notation 9.
On a
W
h(α, β)dµ = hα, βiE .
T M = T F̄ ⊕ ν F̄
et
T M = T F ⊕ (νF ∩ T F̄) ⊕ ν F̄ .
(x, p, t) des coordonnées adaptées à cette décomposition.
t dénit des coordonnées locales sur W .
On notera aussi y = (p, t) de manière que (x, y) sont des coordonnées locales
adaptées au feuilletage F .
X
∂α
aα (y) α1
On écrit D sous la forme D =
α
∂y1 ...∂yq q
On note
La coordonnée
|α|≤m
aα (y) ∈ hom(E(x,y) , E(x,y) ) (localement sur
∞
s'identie à une matrice de MN (C (U/F))).
où
Lemme 5.
(i) Le bré vectoriel
π ∗ (Ē)
un ouvert
U
de
M , aα (y)
s'identie à un sous-bré de
∗
(ii) Le bré vectoriel π (Ē) est stable par
E.
aα (y).
Démonstration.
(i) Soient evm : Ēπ(m) → Em , σ 7→ σ(m),
ev : π ∗ (Ē) → E, (m, σ) 7→ σ(m).
Comme l'application evm est linéaire pour tout m de M , ev = (evm )m∈M
et
est un morphisme de brés vectoriels.
σ ∈ Γ(Lt , E/F), si σ(x,p,t) = 0 alors comme σ est basique on a
que σ = 0 (voir démonstration de la proposition 46 page 53).
∗
Donc ev(x,p,t) est injective et π (Ē) s'identie à un sous-bré de E .
∗
(ii) Soit σ ∈ π (Ē)(x,p,t) = Γ(Lt , E/F).
∗
Montrons que aα (y)(σ) ∈ π (Ē)(x,p,t) .
∞
Localement aα (y) s'identie à une matrice de MN (C (U/F)),
or une fonction basique est constante le long des feuilles de F ,
donc constante le long des feuilles de F̄ .
Par conséquent les coecients de la matrice aα sont indépendants de
∗
∗
la coordonnée p, et aα (p, t)(σ) ∈ π (Ē)(x,p,t) . Ainsi π (Ē) est stable
par aα (p, t).
Soit
Remarque.
sur
aα (p, t) sont indépendants
p, on notera ãα (t) l'application linéaire induite par aα (p, t)
Comme les coecients de la matrice
de la coordonnée
π ∗ (Ē).
De plus si
s ∈ Γ(Ē),
Proposition 50.
on a
ψ ◦ aα (p, t) ◦ ψ −1 (s) = ãα (t)(s).
D̄ = ψ ◦ D ◦ ψ −1
X
σ(D̄)(t, η) =
ãα (t)η1α1 ...ηkαk
Sous les mêmes hypothèses,
opérateur diérentiel d'ordre
m
et
|α|=m
55
est un
η ∈ Tt∗ W , k = dim W et on identie T ∗ W à un sous-espace de ν ∗ F .
En particulier si D est F -transversalement elliptique, alors D̄ est elliptique.
où
Démonstration.
T ∗W ∼
= (ν F̄)∗ ,
{ξ ∈
= 0, ∀X ∈ Γ(T F̄)}.
∗
∈ T M/ξ(X) = 0, ∀X ∈ Γ(T F)},
=
∗
∗
donc T W s'identie à un sous-bré de ν F .
Soit U une carte locale de W et r le rang du bré Ē .
En utilisant des trivialisations locales on a que Γ(Ē|U ) ∼
= C ∞ (W )r c'est-à∞
dire Γ(Ē|U ) est un module libre de rang r sur C (W ).
Soient s1 , ..., sr des sections de Γ(Ē|U ) qui engendrent Γ(Ē|U ).
−1
On note σi = ψ
(si ). Comme ψ : Γ(E/F) → Γ(Ē) est un isomorphisme,
Γ(E/F) est un module libre de rang r sur C ∞ (M/F) engendré par σ1 , ..., σr .
r
r
X
X
−1
∞
Soient gi ∈ C (W ), si s =
gi (t)si alors ψ(s)
=
gi (π(p, t))σi , et si
∗
donc T W ∼
=
∗
∼
Or ν F
{ξ
n
X
σ=
On a
T ∗ M/ξ(X)
i=1
fi σi
avec
fi
basique, alors
ψ(σ) =
i=1
sur
W
r
X
i=1
f˜i (t)si
où
f˜i
est la fonction
i=1
induite par
fi
le long des feuilles de
(comme
F
fi
est une fonction basique, elle est constante
et donc par continuité constante sur les feuilles de
F̄ ).
Soit
s=
r
X
gi (t)si ∈ Γ(Ē|U ),
comme
ψ −1 (s)
est basique on peut calculer
i=1
D(ψ −1 (s))
sur un ouvert adapté aux feuilletages
56
F
et
F̄ .
On note
(x, y)
avec
y = (p, t)
les coordonnées locales sur cet ouvert, on a
D̄(s) = ψ ◦ D ◦ ψ −1 (s)
r
X
=
ψ ◦ D ◦ ψ −1 (gi (t)si )
i=1
=
r
X
ψ ◦ D(gi (π(p, t))ψ −1 (si ))
i=1
r
X
X
∂α
=
α gi (π(p, t))
∂y1α1 ...∂yq q
i=1 |α|≤m
r
X
X ∂α
−1
=
ψ aα (p, t)ψ (si ) α1
gi (π(p, t))
∂t1 ...∂tαk k
ψ aα (p, t)ψ −1 (si )
i=1 |α|≤m
(car gi (π(p, t)) est indépendante de p)
r
X
X
∂α
=
ãα (t)(si ) α1
gi (t)
∂t1 ...∂tαk k
i=1 |α|≤m
X
=
ãα (t)
|α|≤m
∂α
(s).
∂tα1 1 ...∂tαk k
D̃ est unX
opérateur diérentiel d'ordre m
σ(D̄)(t, η) =
ãα (t)η1α1 ...ηkαk , ∀η ∈ Tt∗ W .
Donc
|α|≤m
∗
Comme T W s'identie à un sous-espace de
de
aα (p, t),
on déduit que
D̄
ν ∗F
et
et que
ãα (t) est la restriction
est elliptique.
Théorème 16.
Si s ∈ N, l'opérateur D se prolonge en un opérateur de
D : H s (E/F) → H s−m (E 0 /F) dont l'indice est indépendant de s.
notera indB (D) l'indice de Fredholm de D et on a indB (D) = ind(D̄).
Fredholm
On
Démonstration.
L'opérateur D̄ est elliptique et la variété W est compacte,
D̄ : H s (Ē) → H s−m (Ē 0 ).
s
Or Γ(E/F) et Γ(Ē) sont isométriquement isomorphes, donc H (E/F) et
s
H (Ē) sont isomorphes.
Comme D et D̄ sont conjugués on obtient le résultat voulu.
donc
Théorème 17.
Si de plus l'opérateur
(i) les espaces propres de
D
D
est auto-adjoint,
sont de dimension nie et formés de sections
C ∞,
D est une suite qui tend en vadit D est un opérateur à résolvante
(ii) L'ensemble des valeurs propres de
leur absolue vers
+∞
(autrement
compacte),
(iii)
L2 (M, E/F)
est la somme hilbertienne des espaces propres de
57
D,
(iv) si
c
(λk )k
est la suite des valeurs propres de
alors
m
λk ∼ ck dim W
où
est une constante.
Démonstration.
cation
D,
Les opérateurs
ψ : Γ(E/F) → Γ(Ē)
D
et
D̄
sont conjugués au travers de l'appli-
qui est un isomorphisme isométrique, donc
D̄∗ sont conjugués. Les propriétés valent pour les opérateurs
or D est conjugué à D̄ et l'opérateur D̄ est elliptique,
donc elles valent aussi pour D .
et
Théorème 18.
Si de plus l'opérateur
D
D∗
elliptiques,
est auto-adjoint, on a une décom-
2
position L -orthogonale
Γ(E/F) = ker D ⊕ ImD
où
ker D
est de dimension nie.
Démonstration.
Découle des résultats précédents.
Théorème 19.
à
λ.
On note
dλ
la dimension de l'espace propre de
D
associé
Comme dans le cas général (étudié dans le premier chapitre), on peut
dénir l'opérateur
trD−s =
X dλ
λ>0
λs
Démonstration.
D−s .
Si
m>0
et
s>
dim W
,
m
alors
D−s
est traçable et
.
Découle des résultats précédents.
On revient à présent au cas où
F
est riemannien et transversalement
orientable.
On note
M]
le bré des repères orthonormés transverses et
F]
le feuilletage
relevé.
Le feuilletage
(M ] , F ] )
est un feuilletage transversalement parallélisable, on
]
notera W la variété basique de
Le groupe
H = SO(q) agit
W ].
(M ] , F ] ) et on suppose que dim W ] > 0.
]
]
sur (M , F ) et préserve les feuilles, donc H
induit une action sur
Proposition 51.
On note
E]
le relevé de
E
sur
M ].
]
]
Le bré E est un F -bré hermitien H -équivariant.
]
]
On note Ē le bré utile associé au bré E , alors l'action de
]
de manière naturelle une action de H sur Ē .
Démonstration.
sur
E]
sur
E]
induit
ρE : E ] → E la projection induite par ρ : M ] → M .
]
par ρE de la connexion ∇ sur E est une connexion ∇
Soit
L'image réciproque
H
qui en fait un bré feuilleté.
58
On a alors un diagramme commutatif où toutes les applications sont feuilletées :
E]
ρE
- E
q
q]
?
M]
ρ
?
- M
∇] est donc basique et compatible avec la métrique hermitienne
h.
]
D'autre part l'action de H sur M se relève à l'aide de cette connexion en
]
une action sur E qui préserve à la fois le feuilletage FE ] et la métrique
]
hermitienne h
La connexion
h] sur
E ] relevée de
Remarque.
(i) On a les isomorphismes suivants :
C ∞ (M/F) ∼
= C ∞ (M ] /F ] )H ∼
= C ∞ (W ] )H .
Γ(E ] /F ] )
(ii) Comme
est isomorphe à
Γ(Ē ] ),
on a
Γ(E/F) ∼
= Γ(E ] /F ] )H ∼
= Γ(Ē ] )H .
Γ(E/F) par restriction à Γ(E ] /F ] )H
]
]
précédemment sur Γ(E , F ) à l'aide de la mé-
(iii) On dénit le produit scalaire sur
de celui déni comme
trique
h]
.
Dénition 54.
L'opérateur D se relève en un opérateur diérentiel basique
H -invariant D] : Γ(E ] /F ] ) → Γ(E 0] /F ] ) tel que le diagramme suivant est
commutatif :
Γ(E ] /F ] )H
D]-
∼
=
∼
=
?
Γ(E/F)
Proposition 52.
Γ(E 0] /F ] )H
D
?
- Γ(E 0 /F)
H on dénit un
H -invariant ∆H qui s'annule sur Γ(E ] /F ] )H
0
(où 2m est l'ordre de D ) est transversalement
En utilisant les champs fondamentaux de
opérateur diérentiel d'ordre 2
D0 = D] + (∆H )m
et tel que
0
elliptique.
Démonstration.
Voir [EKA90].
Proposition 53.
Alors
D̄0
On note
D̄0
l'opérateur induit par
D0
est un opérateur diérentiel elliptique d'ordre
Démonstration.
sur
W ].
m.
Il sut d'appliquer la proposition 50 page 56.
59
Théorème 20.
Si s ∈ N, l'opérateur D se prolonge en un opérateur de
D : H s (E/F) → H s−m (E 0 /F) dont l'indice est indépendant de s.
On notera indB (D) l'indice de Fredholm de D , qu'on appellera l'indice ba0H
0H désigne la restriction à
sique de D . On a alors indB (D) = ind(D̄ ) où D̄
]
H
Γ(Ē ) .
Fredholm
Démonstration.
Comme
F]
est transversalement parallélisable,
on sait d'après le théorème 16 (page 57) que
s
]
]
]
sur H (M , E /F ). Or l'opérateur
D
D]
se prolonge en un opérateur
est conjugué à
]
D],H = D|Γ(E
] /F ] )H et
D̄0H . L'action de H sur Γ(E ] /F ] ) se prolonge en une action de H
s
]
]
]
],H aux sections invariantes par
sur H (M , E /F ). Donc en restreignant D
s
]
]
]
H de H (M , E /F ) on obtient un prolongement de D sur H s (M, E/F).
Le deuxième point découle immédiatement du fait que D est conjugué à
D̄0H .
donc à
Théorème 21.
Si de plus
D
(i) Les espaces propres de
est auto-adjoint on a :
D sont de dimension nie et formés de sections
C ∞.
D est une suite de valeurs propres
+∞ (autrement dit D est un opérateur
(ii) L'ensemble des valeurs propres de
qui tend en valeur absolue vers
à résolvante compacte).
L2 (E, M/F) est la somme hilbertienne des espaces propres de D.
(iv) Si (λk )k est la suite des valeurs propres de D , il existe une constante
m
c > 0 telle que λk ≥ ck dim W ] .
(iii)
Démonstration.
L'application
ψ : Γ(E/F) → Γ(Ē) est un isomorphisme
H , donc (D],H )∗ et (D̄0H )∗ sont
isométrique qui commute avec l'action de
conjugués. Les propriétés sont vériées pour les opérateurs elliptiques,
or
D
est conjugué à
D̄0
H
qui est la restriction d'un opérateur elliptique,
donc le résultat est vrai pour
Théorème 22.
Si de plus
D
D.
est auto-adjoint, on a une décompositon
L2 -
orthogonale :
Γ(E/F) = ker D ⊕ ImD
ker D
où
est de dimension nie.
Démonstration.
La décomposition est vraie pour l'opérateur
D̄0 induit par D0
W ] . Comme D est conjugué à D̄0H il sut de restreindre la décomposition
0
induite par D̄ aux sections invariantes pour obtenir le résultat voulu.
sur
Théorème 23.
λ.
Si
m>0
et
dλ la dimension de l'espace propre de D associé
X dλ
dim W ]
−s est traçable et trD −s =
s>
, alors D
.
m
λs
On note
λ>0
Démonstration.
Découle des résultats précédents.
60
à
Remarque.
Etudions à présent le cas où la variété basique
W
est de di-
mension nulle.
Proposition 54.
Le feuilletage
]
si et seulement si dim W
Démonstration.
Si
F
(M ] , F ] )
est un feuilletage à feuilles denses
= 0.
est un feuilletage à feuilles denses,
M appartiennent à l'adhérence de la même feuille,
dim W ] = 0.
]
Si dim W = 0 alors tous les points de M appartiennent à l'adhérence de la
]
même feuille, donc F est un feuilletage à feuilles denses.
alors tous les points de
et donc
Proposition 55.
Si
dim W ] = 0,
ind(D)
Démonstration.
alors
= dim Γ(E ] /F ] )H − dim Γ(E 0] /F ] )H .
= ind(D],H ), car ces deux opérateurs sont
]
]
conjugués. Comme le feuilletage (M , F ) est un feuilletage à feuilles denses,
]
]
]
0]
]
on sait que ind(D ) = dim Γ(E /F ) − dim Γ(E /F ) (voir proposition 46
On a ind(D)
page 52).
Donc ind(D)
= ind(D],H ) = dim Γ(E ] /F ] )H − dim Γ(E 0] /F ] )H .
Remarque. Dans le cas où le feuilletage F n'est pas transversalement orientable les résultats précédents restent valable, il sut de remplacer partout
le groupe
H = SO(q)
Problème ouvert.
par
O(q).
Calculer l'indice basique en fonction d'invariants trans-
verses au feuilletage.
4.2 Le Laplacien basique
Etudions à présent le cas du Laplacien basique (voir [EKA90, PR96,
KT87]).
Dénition 55.
On note P la projection orthogonale de
L2 (Ω∗ (M ))
sur
L2 (Ω∗ (M/F)).
Proposition 56.
Démonstration.
Dénition 56.
P (Ω∗ (M )) ⊂ Ω∗ (M/F).
Voir [PR96].
On note
diérentielle de de Rham
dB : Ω∗ (M/F) → Ω∗ (M/F)
aux formes basiques et δB son
la restriction de la
adjoint formel.
On appelle Laplacien basique l'opérateur
∆B = dB δB + δB dB : Ω∗ (M/F) → Ω∗ (M/F).
61
Remarque.
δB = P ◦ δ , où δ désigne l'adjoint formel de la
P ◦ d ◦ P = d ◦ P , on a P ◦ δ ◦ P = P ◦ δ .
δB ◦ P = P ◦ δ = δB .
On a
diérentiel
de de Rham. Comme
Donc
Proposition 57.
Le Laplacien basique
∆B
est un opérateur diérentiel
basique d'ordre 2 fortement transversalement elliptique.
Démonstration.
Comme
dB
est un opérateur diérentiel basique d'ordre 1,
il en est de même de son adjoint formel
Donc
∆B
δB .
est un opérateur diérentiel basique d'ordre 2.
Le calcul du symbole principal est similaire au cas général,
donc
σ(∆B )(z, ξ) = ||ξ||2 .
Remarque.
Nous allons calculer explicitement l'opérateur
une expression explicite pour le Laplacien basique
Proposition 58.
est la
∆B
δB
et en déduire
(voir [PR96]).
∀β ∈ Ωk (M/F), δB (β) = (−1)q(k+1)−1 ¯∗(d − κ∧)¯∗β ,
codimension du feuilletage et κ la forme de courbure principale.
où
q
Démonstration.
hdγ, βiM
Z
=
dγ ∧ ∗β
M
Z
=
dγ ∧ ¯
∗ β ∧ χF
M
Z
=(−1)k
γ ∧ d(¯
∗β ∧ χF )
ZM
=(−1)k
γ ∧ (d¯
∗β ∧ χF + (−1)q−k ¯∗β ∧ dχF )
M
Z
k
=(−1)
γ ∧ (d¯
∗β ∧ χF + (−1)q−k ¯∗β ∧ (−κ ∧ χF + ϕ0 ))
ZM
k
=(−1)
γ ∧ (d¯
∗β ∧ χF + (−1)q−k+1 ¯∗β ∧ κ ∧ χF ) + (−1)q−k γ ∧ ¯∗β ∧ ϕ0
ZM
k
=(−1)
γ ∧ (d¯
∗β ∧ χF − κ ∧ ¯∗β ∧ χF ) + (−1)q−k γ ∧ ¯∗β ∧ ϕ0
M
62
or
γ∧¯
∗β
est basique, donc
γ ∧ ¯∗β ∧ ϕ0 = 0
(voir proposition 44 page 46).
Donc
hdγ, βiM
Z
k
γ ∧ ((d¯
∗β − κ ∧ ¯∗β) ∧ χF )
=(−1)
M
Z
γ ∧ ∗2 ((d¯∗β − κ ∧ ¯∗β) ∧ χF )
=(−1)k+k(k−1)(n−k+1)
M
Z
k+k(k−1)(n−k+1)+p(n−p−(n−p−k+1))
γ ∧ ∗(¯∗(d¯∗β) − ¯∗(κ ∧ ¯∗β))
=(−1)
M
Z
(n−p)(k+1)+1
γ ∧ ∗(¯∗(d¯∗β) − ¯∗(κ ∧ ¯∗β))
=(−1)
ZM
< γ, (¯∗(d¯∗β) − ¯∗(κ ∧ ¯∗β) >g dvol
=(−1)(n−p)(k+1)+1
M
puisque
q = n − p.
Corollaire 5.
∀β ∈ Ωk (M/F), δB (β) = ((−1)q(k+1)−1 ¯∗d¯∗ + κy )(β)
où
y
désigne le produit intérieur.
Démonstration.
β ∈ Ωk (M/F) et α ∈ Ωk−1 (M/F). Par la proposition
q(k+1) ¯
montrer que (−1)
∗(κ ∧ ¯∗β) = κy (β).
Soient
précédente il sut de
hα, κy (β)iM = hκ ∧ α, βiM
Z
k−1
= (−1)
κ ∧ α ∧ ∗β
M
Z
= (−1)k−1
α ∧ κ ∧ ∗β
dvol
dvol
M
Z
= (−1)k−1+(q−k+1)(q−(q−k+1))
α ∧ κ ∧ ∗¯β ∧ χF dvol
M
Z
(k−1)(q−k+2)
= (−1)
α ∧ ¯∗(¯∗(κ ∧ ¯∗β)) ∧ χF dvol
Z M
α ∧ ∗(¯∗(κ ∧ ¯∗β))dvol
= (−1)(k−1)(q−k)
M
D
E
= α, (−1)(k−1)(q−k) ¯∗(κ ∧ ¯∗β)
.
M
(k − 1)(q − k) ≡ q(k + 1) mod2
q(k+1) ¯
donc (−1)
∗(κ ∧ ¯
∗β) = κy (β).
Or
Corollaire 6.
P ◦ δ = δ ◦ P + (−1)p (ϕ0 )y ◦ (χF ∧ .) ◦ P
Démonstration.
hα, δP βiM
β ∈ Ωk (M/F)
= hdα, P βiM
Soit
et
α ∈ Ωk−1 (M/F).
63
De la même manière que pour la démonstration précédente, comme
Pβ
est
basique on a
k
hdα, P βiM = (−1)
Z
α∧(d¯∗P β∧χF −κ∧¯∗P β∧χF )+(−1)q−k α∧¯∗P β∧ϕ0 .
M
Donc
hα, δP βiM
Z
k
= (−1)
α ∧ (d¯
∗P β ∧ χF − κ ∧ ¯∗P β ∧ χF ) + (−1)(q−k)p α ∧ ϕ0 ∧ ¯∗P β
M
Z
=
α ∧ ∗δB P β + (−1)k α ∧ ϕ0 ∧ ∗(P β ∧ χF )
M
Z
k(p+1)
α ∧ ϕ0 ∧ ∗(χF ∧ P β)
= hα, δB P βiM + (−1)
M
Z
α ∧ ∗2 (ϕ0 ∧ ∗(χF ∧ P β))
= hα, δB P βiM + (−1)k(p+1)+(k−1)(n−k+1)
M
Z
k(p+1)+(k−1)(p+q−k+1)
α ∧ ∗2 (ϕ0 ∧ ∗(χF ∧ P β))
= hα, δB P βiM + (−1)
M
Z
α ∧ ∗2 (ϕ0 ∧ ∗(χF ∧ P β)).
= hα, δB P βiM + (−1)k(q−k)−(p+q−k+1)
M
Or
∀γ ∈ Ωr (M ), ∀ω ∈ Ωs (M ), γy (ω) = (−1)(s−r)(n−s) ∗ (γ ∧ ∗ω),
donc
Z
α ∧ ∗2 (ϕ0 ∧ ∗(χF ∧ P β))
M
Z
k(q−k)−(p+q−k+1)+(p+k−(p+1))(n−(p+k))
α ∧ ∗((ϕ0 )y (χF ∧ P β)).
= (−1)
k(q−k)−(p+q−k+1)
(−1)
M
Par ailleurs
k(q − k) − (p + q − k + 1) + (p + k − (p + 1))(n − (p + k))
≡ k(q − k) − n + k − 1 + (k − 1)(q − k)
≡ (q − k)(k + k − 1) − n + k − 1
≡k−q−n+k−1
≡p−1
mod2
mod2
mod2
mod2
hα, δP βiM = hα, δB P βiM − (−1)p hα, (ϕ0 )y (χF ∧ P β)iM .
p
Donc δP = δB P − (−1) (ϕ0 )y (χF ∧ .) ◦ P ,
or δB ◦ P = P ◦ δ = δB .
p
Donc P ◦ δ = δ ◦ P + (−1) (ϕ0 )y ◦ (χF ∧ .) ◦ P .
donc
64
Remarque. On note = (−1)p (ϕ0 )y ◦(χF ∧.). Donc on a P ◦δ = δ◦P +◦P .
est un opérateur diérentiel
⊂ Ω∗ (M/F)⊥ . En eet :
P ◦δ =δ◦P +◦P
donc P ◦ δ = P ◦ δ ◦ P + P ◦ ◦ P
or P ◦ d ◦ P = d ◦ P
donc P ◦ δ ◦ P = δ ◦ P
donc P ◦ ◦ P = 0.
L'opérateur
d'ordre 0 qui vérie
(Ω∗ (M/F))
Corollaire 7.
On a
Démonstration.
d ◦ P = P ◦ d + (−1)p P ◦ (χFy ) ◦ (ϕ0 ∧ .).
Il sut de prendre l'adjoint dans le corollaire précédent.
Théorème 24.
(i) Sur
Ω∗ (M/F)
on a
∆B = ∆ + ◦ d + d ◦ .
(ii) On a la relation suivante entre le Laplacien basique et le Laplacien
usuel :
˜ ◦P =P ◦∆
¯ ◦P
∆B ◦ P = ∆
˜ =∆+◦d+d◦
∆
où
Démonstration.
(i) Soit
et
¯ = ∆ + ∗ .
∆
β ∈ Ω∗B (M ),
on a
∆B (β) = (P δd + dP δ)(β)
= (P δP d + dP δP )(β)
= ((δP + P )d + d(δP + P ))(β)
= ((δ + )d + d(δ + ))(β)
= (∆ + ◦ d + d ◦ )(β).
(ii)
˜ ◦ P = P ∆P
˜
∆
= P (∆ + d + d)
= P ∆P + P dP + P dP
= P ∆P + P P dP + (dP − P ∗ )P.
(Ω∗ (M/F)) ⊂ Ω∗ (M/F)⊥ ,
∗
˜ ◦ P = P ∆P − P ∗ P = P ∆P
¯ .
donc P P = 0 et ∆
Or
Théorème 25.
dant de
s ∈ N, le Laplacien basique ∆B se prolonge en un opéra∆B : H s (M/F) → H s−2 (M/F) dont l'indice est indépen-
Si
teur de Fredholm
s.
65
Démonstration.
Il sut d'appliquer le théorème 16 page 57 sur les opérateurs
transversalement elliptiques.
Théorème 26.
(i) Les espaces propres de
et formés de sections
∆B
sont de dimension nie
C ∞.
∆B est une suite tendant vers +∞
∆B est un opérteur à résolvante compacte).
L2 (Ω∗ (M/F)) est la somme hilbertienne des espaces propres de ∆B .
(ii) L'ensemble des valeurs propres de
(autrement dit
(iii)
2
(iv) Si
où
c
(λk )k
est la suite des valeurs propres de
∆B ,
on a
λk ≥ ck dim W ]
est une constante.
Démonstration.
Il sut d'appliquer le théorème 17 page 57 sur les opérateurs
transversalement elliptiques.
Remarque.
L'asymptotique du spectre du Laplacien basique permet d'étu-
dier le noyau de la chaleur basique (voir [Ton97, NRT90, PR96, Ric10,
Ric98]).
Dénition 57.
Un élément de
On note
H∗ (M/F)
H∗ (M/F) = ker ∆B .
est appelé une forme basique harmonique.
Théorème 27 (Décomposition de de Rham-Hodge basique).
On a une dé-
composition orthogonale
Ω∗ (M/F) = H∗ (M/F) ⊕ Im∆B = H∗ (M/F) ⊕ ImdB ⊕ ImδB ,
où
H(M/F)
est de dimension nie.
Démonstration.
Il sut d'appliquer le théorème 18 page 58 sur les opérateurs
transversalement elliptiques.
Corollaire 8.
La cohomologie basique
Démonstration.
H ∗ (M/F)
Comme dans le cas classique (voir corollaire 1) la décompo-
sition de de Rham-Hodge basique implique
Donc
est de dimension nie.
H ∗ (M/F) ∼
= H∗ (M/F).
dim H ∗ (M/F) < +∞.
Nous allons à présent étudier la dualité de Poincaré pour la cohomologie
basique. Pour cela nous allons rappeler quelques résultats importants en
renvoyant le lecteur aux diérentes références : [EKASH85, Ser85, EKAH86,
EKA90, Mas92, AL92, Dom98].
Proposition 59. La cohomologie basique en dimension maximale H q (M/F)
est soit isomorphe à
R,
soit isomorphe à
Démonstration.
Voir [EKASH85].
Dénition 58.
On dit que le feuilletage
q
si H (M/F)
6= 0.
66
0.
F
est homologiquement orientable
Théorème 28.
ment si
sur
M
F
Le feuilletage
F
est homologiquement orientable si et seule-
est minimalisable, c'est-à-dire il existe une métrique quasi-brée
tel que les feuilles de
F
sont des sous-variétés minimales.
Démonstration.
Voir [Mas92, AL92].
Théorème 29.
Le feuilletage
F
est homologiquement orientable si et seule-
ment s'il existe un métrique quasi-bré sur
principale
κ
Remarque.
tel que la forme de courbure
est nulle.
Démonstration.
des feuilles
M
Voir [Dom98].
En particulier pour une telle métrique la forme volume le long
χF
est
Proposition 60.
F -fermée, c'est-à-dire dχF (V1 , ..., Vp+1 ) = 0 si Vi ∈ Γ(T F).
F est homologiquement orientable.
¯∗ : Ωk (M/F) → Ωq−k (M/F) vérie
isomorphisme ¯
∗ : Hk (M/F) → Hq−k (M/F).
On suppose que
Alors l'opérateur de Hodge basique
¯∗∆B = ∆B ¯
∗
et induit un
Démonstration.
Comme
cipale du feuilletage
κ
F
est homologiquement orientable, la courbure prin-
est nulle (voir [Dom98]).
δB =
∆B = (−1)q(k+1)−1 ¯
∗dB ¯
∗dB + dB ¯∗dB ¯∗.
q(k+1)−1 ¯
Donc (−1)
∗∆B = ¯
∗¯
∗dB ¯∗dB + ¯∗dB ¯∗dB ¯∗ et
q(k+1)−1
(−1)
∆B ¯
∗=¯
∗dB ¯
∗dB ¯∗ + dB ¯∗dB ¯∗¯∗.
Comme on a ¯
∗2 = (−1)k(q−k) Id, on a ¯∗∆B = ∆B ¯∗.
En appliquant le corollaire 5 page 63 on a alors
Théorème 30
.
(Dualité de Poincaré)
(−1)q(k+1)−1 ¯∗dB ¯∗, d'où
Si le feuilletage
F
est homologique-
ment orientable, alors on a un isomorphisme
H k (M/F) ∼
= H q−k (M/F).
Démonstration.
Remarque.
Découle de la proposition précédente.
(i) Ce résultat a d'abord été montré par B. Reinhart [Rei59b]
sans l'hypothèse de l'orientation homologique. Mais en 1981 Y. Carrière [Car84] a construit un feuilletage riemannien qui ne satisfait pas
la dualité de Poincaré.
(ii) Ce résultat a été démontré par une méthode diérente dans [Ser85,
EKAH86].
4.3 L'opérateur de de Rham basique
Dénition 59.
DB = dB + δB , Ωpair (M/F) = ⊕k pair Ωk (M/F)
Ωimpair (M/F) = ⊕k impair Ωk (M/F).
Soient
On appelle opérateur de de Rham basique l'opérateur
+
DB
: Ωpair (M/F) → Ωimpair (M/F) qui est la restriction de DB
67
à
et
Ωpair (M/F).
Proposition 61.
L'opérateur de de Rham basique est un opérateur dié-
rentiel basique d'ordre 1 transversalement elliptique.
De plus si
s ∈ N, l'opérateur de de Rham basique se prolonge en un opérateur
+
DB
: H s (M/F) → H s−1 (M/F) dont l'indice est indépendant
de Fredholm
de
s.
Démonstration.
2
On a DB = ∆B et ∆B est transversalement elliptique,
+
donc DB est transversalement elliptique.
Pour le deuxième point il sut d'appliquer les résultats sur les opérateurs
transversalement elliptiques.
Dénition 60.
On appelle caractéristique d'Euler basique l'entier relatif
noté et déni par
χ(M/F) =
q
X
(−1)i dimH i (M/F).
i=1
Proposition 62.
+
L'indice de l'opérateur de de Rham basique indB (DB ) est
donné par la caractéristique d'Euler basique
χ(M/F).
Démonstration.
Comme dans la cas classique,
le noyau de
est
+
DB
Donc le noyau de
+
= ker(∆B )|Ωpair (M/F ) .
ker DB
+
DB est l'espaces des formes harmoniques
paires.
Comme l'espace des formes harmoniques est isomorphe à la cohomologie de
+
H ∗ (M/F), on a dim ker DB
= dim H pair (M/F).
+ ∗
impair
(M/F).
De même on a dim ker(DB ) = dim H
+
Donc indB (DB ) = χ(M/F).
de Rham
Exemple 9.
Dans le cas d'un feuilletage par bration
H ∗ (M/F) ∼
= H ∗ (B).
Donc la caractéristique d'Euler basique de
sitque d'Euler de la variété
Exemple 10.
(M, F)
π : M → B,
on a
est égale à la caractéri-
B.
Dans le cas d'un feuilletage par suspension
H ∗ (M/F) ∼
= H ∗ (T )G . Donc la caractéristique
q
X
est égale à χ(T /G) =
(−1)k dim H k (T /G).
a
M = B̃ × T /Γ, on
(M, F)
d'Euler basique de
k=1
4.4 L'opérateur de signature basique
Proposition 63.
Si
F
est homologiquement orientable, on munit d'une
métrique quasi-brée telle que
Alors
[ν] 6= 0,
c'est-à-dire
[ν]
κ
est nulle.
engendre
H q (M/F).
68
Démonstration.
Par l'absurde, supposons que
ν = dα
où
α ∈ Ωq−1 (M/F).
On a
dα ∧ χF = dα ∧ χF + (−1)q−1 α ∧ dχF
= ν ∧ χF + (−1)q−1 α ∧ dχF
= dvol + (−1)q−1 α ∧ dχF
χF ∈ Ωp,0 (M ) et dχF = dF χF + dt χF + ρ
p+1,0 (M ) = {0}, d χ ∈ Ωp,1 (M ) et ρ ∈ Ωp−1,2 (M ).
où dF χF ∈ Ω
t F
Comme κ = 0, la forme carctéristique χF est F -fermée, donc dt χF = 0 et
dχF = ρ.
0,q−1 (M ) et α ∧ dχ = α ∧ ρ,
Or α ∈ Ω
F
p−1,q+1 (M ) = {0} et α ∧ dχ = 0.
donc α ∧ dχF ∈ Ω
F
n
Donc d(α ∧ dχF ) = dvol et [dvol] = 0 dans H (M ) (ce qui est contradictoire
n
puisque M est orientée et H (M ) est engendré par [dvol]).
q
Donc [ν] 6= 0 dans H (M/F).
Or
Remarque.
La forme volume transversale
ν
est donc une forme basique
harmonique.
Exemple 11.
Dans le cas d'un feuilletage par bration π : M → B , on a
∼
= H k (B), donc (M, F) est un feuilletage homologiquement orientable si et seulement si la variétée B est orientable.
Ici la notion d'orientation transverse de F coïncide donc avec la notion
d'orientation homologique de F .
H k (M/F)
Proposition 64.
q = 4l.
On munit
F
On suppose que
M
est homologiquement orientable et
κ est nulle.
H 2l (M/F) × H 2l (M/F) par
d'une métrique quasi-brée telle que
On dénit une forme bilinéaire
QB
sur
Z
ω1 ∧ ω2 ∧ χF .
QB ([ω1 ], [ω2 ]) =
M
Alors
QB
est bien dénie, symétrique et non-dégénérée.
Démonstration.
QB est bilinéaire et symétrique.
2l−1 (M/F) et ω ∈ Ω2l−1 (M/F).
Montrons que QB est bien dénie. Soient α ∈ Ω
2
Montrons que QB (dα, ω2 ) = 0.
2l−1 α ∧ dω = dα ∧ ω car ω est fermée.
On a d(α ∧ ω2 ) = dα ∧ ω2 + (−1)
2
2
2
Z
Donc
De manière évidente
d(α ∧ ω2 ) ∧ χF .
QB (dα, ω2 ) =
M
4l−1 α ∧ ω ∧ dχ ,
d(α
2
Z ∧ ω2 ∧ χF ) = d(α ∧ Zω2 ) ∧ χF + (−1)
ZF
4l−1
donc
d(α ∧ ω2 ∧ χF ) =
d(α ∧ ω2 ) ∧ χF + (−1)
α ∧ ω2 ∧ dχF .
M
M
M
Z
Selon le théorème de Stokes on a
d(α ∧ ω2 ∧ χF ) = 0,
Or
M
69
Z
α ∧ ω2 ∧ dχF .
QB (dα, ω2 ) =
donc
M
α ∧ ω2 ∈ Ωq−1 (M/F),
Or
donc
α ∧ ω2 ∧ dχF = 0
(voir proposition 44 page
46),
donc
QB (dα, ω2 ) = 0 et QB est bien dénie.
QB est non-dégénérée.
[ωZ1 ] ∈ H 2l (M/F) tel que Z∀[ω2 ] ∈ H 2l (M/F), QB ([ω1 ], [ω2 ]) = 0.
Montrons que
Soit
ω1 ∧ ¯∗¯∗ω2 ∧ χF = 0,
ω1 ∧ ω2 ∧ χF = 0 et
M
M
donc hω1 , ¯
∗ω2 iM = 0.
2l
Donc ∀ω2 ∈ Z (M/F), hω1 , ¯
∗ω2 iM = 0,
2
2l(4l−2l)
or ¯
∗ = (−1)
Id, donc ∀β ∈ Z 2l (M/F), hω1 , βiM
Donc
hω1 , ω1 iM > 0
Or
si
ω1 6= 0,
ω1 = 0
donc
et
QB
Dans la suite du paragraphe on suppose que
orientable,
q = 4l,
Dénition 61.
(M, F)
Dénition 62.
F
et la forme de courbure principale
La signature de
et est notée
QB
= 0.
est non-dégénérée.
est homologiquement
κ
est nulle.
est appelée la signature basique de
σ(M/F).
On note
τ : Ωk (M/F) → Ωq−k (M/F)
l'application dénie
par
τ = (−1)l+
où
¯
∗
k(k−1)
2
¯∗
désigne l'opérateur de Hodge basique.
Proposition 65.
l'opérateur
L'application
τ
est une involution qui anticommute avec
DB = dB + δB .
Démonstration.
On rappelle que
δB = (−1)q(k+1)−1 ¯∗dB ¯∗
puisque
F
est ho-
mologiquement orientable.
Un simple calcul montre alors que
τ
est une involution qui anticommute avec
DB .
Dénition 63.
Ω∗ (M/F) = Ω∗+ (M/F) ⊕ Ω∗− (M/F) où Ω∗+ (M/F)
∗
(respectivement Ω− (M/F)) est l'espace propre de τ associé à la valeur propre
On note
1 ( respectivement -1).
On appelle opérateur de signature basique et on note
DB à Ω∗+ (M/F),
+
DB
Proposition 66.
:
Ω∗+ (M/F)
→
Ω∗− (M/F).
L'opérateur de signature basique
+
DB
+
DB
la restriction de
est un opérateur
diérentiel basique d'ordre 1 transversalement elliptique.
De plus si
s ∈ N, l'opérateur de signature basique se prolonge en un opérateur
+
DB
: H s (M/F) → H s−2 (M/F) dont l'indice est indépendant
de Fredholm
de
s.
70
Démonstration.
La démonstration est similaire au cas de l'opérateur de de
Rham basique. Pour le deuxième point il sut d'appliquer les résultats sur
les opérateurs transversalement elliptiques.
Proposition 67.
L'indice de l'opérateur de signature basique est donné par
la signature basique
Démonstration.
σ(M/F)
(M, F).
de
La démonstration est similaire au cas classique (voir propo-
sition 4).
Proposition 68.
σ(M, F)
Dans le cas d'un feuilletage homologiquement orientable
q = 4k
de codimension
par bration
est égale à la signature de la
sinature basique coïncide donc avec la
π : M → B , la signature basique
variété B . L'indice de l'opérateur de
signature de B .
Lemme 6. On note ∗B l'opérateur de Hodge sur B et ¯∗ l'opérateur de Hodge
basique sur
M.
Démonstration.
Soit
ω ∈ Ωk (B),
π ∗ (∗B ω) = (−1)pq ¯∗(π ∗ (ω)).
X
ωy =
fI (y)dyi1 ∧ ... ∧ dyik ,
on a
On a localement
i1 <...<ik
donc
X
∗B (ωy ) = fI (y)dyj1 ∧ ... ∧ dyjq−k
où
est la signature de la
i1 <...<ik
1
...
q
.
permutation
i1 ... ik j1 ... jq−k
X
π ∗ (∗B (ω))z = fI (π(z))π ∗ (dyJ1 ∧ ... ∧ dyjq−k )
j1 <...<jk
=
X
fJ (π(z))dyj1 ∧ ... ∧ dyjq−k
j1 <...<jk
yj ◦ π = yj .X
∗
Or π (ω)z =
car
fI (π(z))π ∗ (dyi1 ∧ ... ∧ dyik ) =
i1 <...<ik
X
fI (π(z))dyi1 ∧ ... ∧ dyik ,
i1 <...<ik
donc
¯
∗(π ∗ (ω)z ) = (−1)pq ¯
∗(
X
fI (π(z))dx1 ∧ ... ∧ dxp ∧ dyi1 ∧ ... ∧ dyik )
i1 <...<ik
pq 0
= (−1) X
fI (π(z)) ∧ dyj1 ∧ ... ∧ dyjq−k
i1 <...<ik
1
...
n
.
1 ... p i1 ... ik j1 ... jq−k
π ∗ (∗B ω) = (−1)pq ¯∗(π ∗ (ω)).
0
où est la signature de la permutation
= 0 ,
donc
Lemme 7.
On a
On a
Ω∗ (M/F) et
π ∗ ◦ δB .
dB
dBas ◦ π ∗ = π ∗ ◦ dB
où
dBas
la diérentielle de de Rham sur
71
désigne la diérentielle sur
Ω∗ (B).
De plus
δBas ◦ π ∗ =
Démonstration.
Avec les conventions de signe habituelles on a
δBas = (−1)q(k−1)−1 ¯
∗dBas ¯
∗
et
δBas = (−1)q(k−1)−1 ∗ dBas ∗.
π ∗ ◦ ((−1)q(k−1)−1 ∗ dBas ∗) = (−1)q(k−1)−1 (−1)pq (−1)pq (¯∗dBas ¯∗) ◦ π ∗ )
= δBas ◦ π ∗
Démonstration de la proposition 68.
σ(B) =
On sait que
désigne l'opérateur de signature sur la variété
ind(D+ ) où
D+
B.
+
+
σ(M/F) = indB (DB
) où DB
désigne l'opérateur de signature basique
+
sur M . Les lemmes précédents impliquent que les opérateurs D+ et DB sont
conjugués, donc admettent le même indice. Ainsi σ(B) = σ(M/F).
Et
Nous allons étudier la signature basique d'un feuilletage par suspension
M = B̃ × T /Γ.
On rappelle que
Proposition 69.
q2 : M̃ → T
ω ∈ Ωk (T /Γ), on
basique sur M et ∗T
Soit
l'opérateur de Hodge
a
désigne la deuxième projection.
φ(∗T ω) = ¯∗φ(ω),
où
¯∗
désigne
désigne l'opérateur de Hodge sur
T.
Démonstration.
(x1 , ..., xp , y1 , ..., yq ) des coordonnées locales sur M̃
en (x̃, y), donc (y1 , ..., yq ) sont des coordonnées locales en y et
(x1 ◦ π −1 , ..., xp ◦ π −1 , y1 ◦ π −1 , ..., yq ◦ π −1 ) sont des coordonnées locales en
[x̃, y].
X
Localement on a ω =
fI (y)dyi1 ∧ ... ∧ dyiq .
Soient
i1 <...<ik
Montrons que
M̃ .
∗T ω = q2∗ (∗T ω) = (−1)pq ∗B (q2∗ (ω)),
où
∗B
l'opérateur de Hodge ba-
sique sur
On a
X
fI (y)dyi1 ∧ ... ∧ dyiq−k
où
est la signature de la per-
i1 <...<ik
1
...
q
mutation
.
i1 ... ik j1 ... jq−k
Comme yl ◦ q2 = yl , on a
X
q2∗ (∗T ω) = fI (q2 (x̃, y))q2∗ (dyi1 ∧ ... ∧ dyiq−k )
i1 <...<ik
X
=
fI (q2 (x̃, y))dyi1 ∧ ... ∧ dyiq−k
i1 <...<ik
Or
q2∗ (ω) =
X
fI (q2 (x̃, y))dyi1 ∧ ... ∧ dyik ,
i1 <...<ik
donc
X
∗B q2∗ (ω) = (−1)pq 0
fI (q2 (x̃, y))dyi1 ∧ ... ∧ dyiq−k
où
0
i1 <...<ik
gnature de la permutation
1
...
n
1 ... p i1 ... ik j1 ... jq−k
72
.
est la si-
q2∗ (∗T ω) = (−1)pq ∗B (q2∗ (ω)).
k
∗
pq ∗ ∗α).
Selon le lemme 6 page page 71, on a ∀α ∈ Ω (M/F), ∗B π (α) = (−1) π (¯
∗
pq ∗ (π ∗ (φ(ω)),
Ainsi q2 (∗T ω) = (−1)
B
∗
∗
donc π (φ(∗T ω)) = π (¯
∗φ(ω)),
et φ(∗T ω) = ¯
∗φ(ω).
Or
0 = ,
donc
Proposition 70. On note dT la diérentielle sur Ω∗ (T ) et donc sur Ω∗ (T /G)
et
dB
la diérentielle sur
Ω∗ (M/F).
T est munie d'une structure riemannienne G-invariante, l'adjoint
δT de dT se restreint à Ω∗ (T /G).
On a alors δB ◦ φ = φ ◦ δT , en particulier l'opérateur DB = dB + δB est
G
∗
∗
conjugué à D = dT + δT : Ω (T /G) → Ω (T /G).
Comme
formel
Démonstration.
φ ◦ δT = φ ◦ ((−1)q(k−1)−1 ∗T dT ∗ T )
= (∗B (−1)q(k−1)−1 dB ∗B ) ◦ φ
= δB ◦ φ
Corollaire 9.
La signature basique de
(M, F)
est donnée par
σ(M/F) = σ(T /G).
Démonstration.
+
+
désigne l'opéra) où DB
σ(M/F) = indB (DB
teur de signature basique sur M .
G
G
Et σ(M/G) = ind(D+ ) où D+ désigne l'opérateur de signature invariant sur
T.
+
G
On vient de voir que D+ et DB sont conjugués, donc ont le même indice.
Donc σ(M/F) = σ(T /G).
On sait que
4.5 L'opérateur de Dolbeault basique
On suppose que
F
est transversalement holomorphe et pour simplier on
F est homologiquement orientable.
νFC = νF ⊗R C hérite d'une structure complexe dont on notera
supposera que
Alors le bré
J
l'automorphisme associé.
La métrique riemmanienne transverse
g̃(., .) = ((g(., .) + g(J., J.))/2
g
dénit une métrique hermitienne
(c'est-à-dire
g̃(J., J.) = g̃(., .)
sur
νFC
et inva-
F -bré hermitien.
F est hermitien.
riante le long des feuilles) et en fait un
Dans ce cas on dira que le feuilletage
Dénition 64. Comme J 2 = −Id, on a une décomposition en somme directe
νFC = νF(1,0) ⊕νF(0,1) où νF(1,0) et νF(0,1) sont les sous-brés de νF
73
associés
aux valeurs propres
i
et
−i
de
J.
On a alors une décomposition du bré en algèbres extérieures
Λk ν ∗ FC = ⊕r+s=k Λr,s
Dénition 65.
où
Une section basique du
rentielle basique de type
On notera
(r, s).
Λr,s = Λp ν ∗ F(1,0) ⊗ Λq ν ∗ F(0,1) .
Ωr,s (M/F, C)
F -bré Λr,s
est appelée forme dié-
(r, s).
l'espace des formes diérentielles basiques de type
On a de manière évidente
Ωk (M/F, C) = ⊕r+s=k Ωr,s (M/F, C).
Comme dans la cas classique d'une variété complexe, sur les formes basiques
Ωk (M/F, C) la diérentielle d se décompose en la somme de deux opérar,s
r+1,s (M/F) et ∂
¯ : Ωr,s (M/F) → Ωr,s+1 (M/F) qui
teurs ∂ : Ω (M/F) → Ω
vérient les relations
∂ 2 = 0, ∂¯2 = 0,
et
¯ = 0.
∂ ∂¯ + ∂∂
On obtient donc un complexe diérentiel
∂¯
...
- Ωr,s (M/F, C)
∂¯ -
Ωr,s+1 (M/F, C)
appelé complexe de Dolbeault basique du feuilletage
∂¯
- ...
F.
La cohomologie associée sera appellée cohomologie de Dolbeault basique de
F
et notée
H r,s (M/F, C).
Proposition 71.
L'opérateur de Hodge basique induit un isomorphisme
¯∗ : Ωr,s (M/F, C) → Ωq−r,q−s (M/F, C).
00 est l'adjoint
00
∗∂¯
∗, alors δB
On pose δB = −¯
Démonstration.
formel de
∂¯.
Cette preuve est similaire au cas classique qui a été traité
précédemment, nous renvoyons le lecteur à la première partie de ce document.
Proposition 72.
00
00
00 ¯ + ∂δ
¯ 00 .
On notera ∆B l'opérateur déni par ∆B = δB ∂
B
00
L'opérateur ∆B est un opérateur diérentiel basique d'ordre 2 formellement
auto-adjoint et transversalement elliptique.
Démonstration.
Cette preuve est similaire au cas du Laplacien basique et
est omise ici.
Théorème 31.
On note
¯ =0
Hr,s (M/F, C) = {ω ∈ Ωr,s (M/F)/∂ω
et
00
δB
ω = 0} = ker ∆00B .
On a alors les propriétés suivantes :
Hr,s (M/F, C) est de dimension
2
décomposition L -orthogonale
(i) l'espace vectoriel
(ii) on a une
nie,
¯ Im(δ 00 )
Ωr,s (M/F, C) = Hr,s (M/F, C)⊕Im(∆00B ) = Hr,s (M/F, C)⊕Im(∂)⊕
B
74
(iii) l'espace vectoriel
H r,s (M/F) est isomorphe à Hr,s (M/F, C) et donc
de dimension nie.
Démonstration.
Il sut d'appliquer les résultats sur les opérateurs trans-
versalement elliptique pour les deux premiers points. La démonstration du
troisième point est similaire au cas de la cohomologie basique.
Théorème 32 (dualité de Serre).
ment orientable, l'application
¯∗
Comme le feuilletage
F
est homologique-
induit un isomorphisme de
H r,s (M/F)
sur
H r−q,s−q (M/F).
Démonstration.
¯∗ commute avec ∆00B ,
r,s
r−q,s−q (M/F) et donc un
et induit un isomorphisme de H (M/F) sur H
r,s (M/F) sur H r−q,s−q (M/F).
isomorphisme de H
L'opérateur de Hodge basique
4.6 L'opérateur de Dirac basique
Etudions maintenant l'opérateur de Dirac basique ([BKR10a]).
Notation 10.
On note
On identie le bré normal
Cl(νF) = Cl(νF) ⊗ C
νF
avec
T F ⊥.
le bré en algèbre de Cliord au-dessus de
M.
Dénition 66.
Soit
On note toujours
∇
E
un bré en
Cl(νF)-modules
au-dessus de
M.
M la connexion
la connexion de Levi-Civita transverse et ∇
de Levi-Civita.
Soit
h
une métrique hermitienne sur
E
et
∇E
une connexion linéaire sur
E.
ξ ∈ Cl(νx F) sur un élément v ∈ Ex par c(ξ)v .
(E, h, ∇E ) est un bré de Cliord basique si :
(i) Le bré E est un bré feuilleté.
E
(ii) La connexion ∇ est une connexion métrique et basique.
(iii) Pour tout ξ ∈ Cl(νx F), c(ξ) est antisymétrique sur Ex .
(iv) Si X ∈ Ξ(M ), Y ∈ Γ(νF), s ∈ Γ(E),
On note l'action de
On dit que
E
∇E
X (c(Y )s) = c(∇X (Y ))s + c(Y )∇X (s).
Notation 11.
Lemme 8.
Si
Dans la suite
(E, h, ∇E ) désigne un bré de Cliord basique.
Y ∈ Γ(νF) un champ de vecteurs basiques
c(V )s est une section basique de E .
et
s ∈ Γ(E)
une
section basique, alors
Démonstration.
Comme s est basique et Y est feuilleté,
∇E
(s)
=
0
et
∇
(Y ) = 0.
V
V
E
E
Donc ∇V (c(Y )s) = c(∇V (Y ))s + c(Y )∇V (s) = 0.
75
si
V ∈ Γ(T F)
on a
Dénition 67.
Dtr
On appelle opérateur de Dirac transversal l'opérateur noté
obtenue à partir de la composition des applications suivantes :
Γ(E)
(∇E )tr
∼
=-
- Γ(ν ∗ F ⊗ E)
c
Γ(νF ⊗ E)
- Γ(E) ,
∇E : Γ(E) → Γ(T ∗ M ⊗ E) et ∼
=
l'isomorphisme induit par la métrique quasi-brée sur M .
Plus précisément si {e1 , ..., eq } est un repère orthonormée de νF , on a
où
(∇E )tr
est la projection sur
ν ∗F
Dtr =
q
X
de
est
tr
c(ej )(∇E
ej ) .
j=1
Proposition 73.
L'opérateur de Dirac transversal induit un opérateur dif-
férentiel basique d'ordre 1 sur
Γ(E/F).
De plus cet opérateur est transversalement elliptique et son symbole est
donné par
σ(Dtr )(x, ξ) = c(ξ).
Démonstration.
Soit
s ∈ Γ(E/F),
montrons que
Dtr (s)
est une section ba-
sique.
x ∈ M,
Au voisinage d'un point
on choisit un repère local
de champs de vecteurs basiques. Soit
∇E
V (Dtr (s))
=
=
q
X
j=1
q
X
V ∈ Γ(T F),
{e1 , ..., eq }
formé
alors
E tr
∇E
V (c(ej )(∇ej ) (s))
E
E
c(∇V (ej ))∇E
ej (s) + c(ej )∇V (∇ej (s))
j=1
=0
car
ej
Donc
s est une
Γ(E/F).
est un champ de vecteur basique et
Dtr
induit bien un opérateur sur
section basique.
La même démonstration que dans le cas classique (voir proposition 8 page
20) montre que
Dtr
Proposition 74.
est basique et transversalement elliptique.
L'adjoint formel de l'opérateur de Dirac transversal est
(Dtr )∗ = Dtr − c(H)
où
H
désigne le champ de vecteur basique de courbure
principal.
Démonstration.
Soit
{e1 , ..., eq }
un repère local de
76
νF
formé de champs de
vecteurs basiques et
s1 , s2 ∈ Γ(E/F).
On a ponctuellement
h(Dtr (s1 ), s2 )x − h(s1 , Dtr (s2 ))x
=
=
q
X
j=1
q
X
E
h(c(ej )∇E
ej (s1 ), s2 )x − h(s1 , c(ej )∇ej (s2 ))x
E
h(c(ej )∇E
ej (s1 ), s2 )x + h(c(ej )s1 , ∇ej (s2 ))x
j=1
=
q
X
M
h(∇E
ej (c(ej )s1 ), s2 )x − h(c(∇ej (ej ))s1 , s2 )x
j=1
+ h(c(ej )s1 , ∇E
ej (s2 ))x
q
q
X
X
=(
∇ej (h(c(ej )s1 , s2 )))x − h(c(
∇M
ej (ej ))s1 , s2 )x
j=1
q
X
=−
j=1
∇ej (iej ω)x + ω(
j=1
où
q
X
∇M
ej (ej ))x
j=1
ω est la 1-forme basique dénie par ω(X) = −h(c(X)s1 , s2 ), ∀X ∈ Γ(νF).
Donc
h(Dtr (s1 ), s2 ) − h(s1 , Dtr (s2 )) = −
=−
=−
q
X
j=1
q
X
∇ej (iej ω) + ω(
q
X
∇ej (ej ))
j=1
(iej ∇ej + i∇ej (ej ) )ω + ω(
j=1
q
X
q
X
∇ej (ej ))
j=1
iej ∇ej ω.
j=1
{e1 , ..., eq } en un repère orthonormé {e1 , ..., en }
tan
M
de T M . On pose ∇
= ∇ −∇ où ∇M désigne la connexion de Levi-Civita.
1
Soit β ∈ Ω (M/F), calculons δβ ,
On complète localement le repère
δβ = −
=−
=−
n
X
j=1
n
X
j=1
q
X
iej ∇M
ej β
iej ∇ej β −
iej ∇ej β −
j=1
n
X
iej ∇tan
ej β
j=1
n
X
j=q+1
77
iej ∇tan
ej β
On écrit
β
sous la forme
β=
q
X
βk e∗k
où
βk
sont des fonctions basiques. On
k=1
a alors
δβ = −
q
X
iej ∇ej β −
j=1
=−
=−
=−
=−
=−
q
X
j=1
q
X
j=1
q
X
j=1
q
X
j=1
q
X
iej ∇ej β −
iej ∇ej β −
iej ∇ej β −
iej ∇ej β −
n
X
q
X
iej ∇tan
(
βk e∗k )
ej
j=q+1
q
n
X
X
k=1 j=q+1
q
n
X
X
k=1 j=q+1
q
n
X
X
k=1 j=q+1
q
n
X
X
k=1
∗
βk iej ∇tan
ej (ek )
βk iej (
βk iej (
n
X
m=q+1
n
X
∗
∗
∗
h(∇M
ej (ek ), em )em )
∗
∗ ∗
h(∇M
ej (em ), ek )em )
m=q+1
∗
∗
βk h(∇M
ej (ej ), ek )
k=1 j=q+1
iej ∇ej β + iH β,
j=1
où
H
est le champ de vecteurs de courbure principale.
Donc si
β∈
Ω1 (M/F), alors
−
q
X
iej ∇ej β = δβ − iH β .
On a donc
j=1
h(Dtr (s1 ), s2 ) − h(s1 , Dtr (s2 )) = −
q
X
iej ∇ej ω
j=1
= δω − iH ω
= δω + h(c(H)s1 , s2 )
= δω − h(s1 , c(H)s2 ).
Comme dans le cas général (voir proposition 9 page 21),
on a donc
hDtr (s1 ), s2 i − hs1 , Dtr (s2 ) − c(H)s2 i = 0.
D'où le résultat.
Remarque.
Si le feuilletage
F
est homologiquement orientable, le forme de
courbure principal et donc le champ de vecteurs de courbure principale sont
nuls. Par conséquent l'opérateur de Dirac transversal est auto-adjoint.
Dénition 68.
On appelle opérateur de Dirac basique l'opérateur
1
DB = Dtr − c(H) : Γ(E/F) → Γ(E/F).
2
78
Proposition 75.
L'opérateur de Dirac basique est un opérateur diérentiel
basique d'ordre 1, auto-adjoint et transversalement elliptique.
Démonstration.
Découle des résultats précédents.
Théorème 33.
Si E est le bré normal au feuilletage νF ,
∗
∼
on a Cl(νF) = Λν F . Et l'opérateur de Dirac transversal
l'opérateur dB + δB .
2
En particulier Dtr est conjugué au Laplacien basique ∆B .
Démonstration.
est conjugué à
La démonstration est similaire au cas classique (voir propo-
sition 10 page 22).
Remarque.
En munissant
Ω∗ (M/F) ∼
= Γ(Λν ∗ F)
des bonnes graduations,
on retrouve ainsi l' opérateur de de Rham basique et l'opérateur de signature
basique à l'aide de l'opérateur de Dirac transversal.
4.7 Exemples
4.7.1 Exemples de calculs de signature basiques
Exemple 12.
B =
S1, T
On considère le feuilletage par suspension où
= CP2 .
Le groupe fondamental de
morphisme de groupe
sur
T
h : Z → S1
par
1 7→ eiθ
B est alors Z, on dénit le
θ est irrationnel et eiθ agit
où
par
eiθ .[z0 , z1 , z2 ] = [eiθ z0 , z1 , z2 ].
On note
G = S1,
G est l'adhérence de h(π1 (B)) et le calcul de la
(M, F) se ramène au calcul de l'indice de l'opérateur
G.
T restreint aux formes G-invariantes D+
alors
gnature basique de
signature sur
Pour cela nous allons utiliser la formule d'Atiyah-Segal-Singer pour la
side
G-
signature (théorème 8 page 27).
Proposition 76. Soit g ∈ G\{1}, l'ensemble des points xes par g
T g = {[1, 0, 0]} ∪ {[0, z1 , z2 ]/z1 , z2 ∈ C∗ }. En particulier T g = T G .
Démonstration.
est
g.[z0 , z1 , z2 ] = [z0 , z1 , z2 ].
∗
Donc gz0 = λz0 , z1 = λz1 , z2 = λz2 où λ ∈ C .
Donc z0 = 0, (1−λ)z1 = 0, (1−λ)z2 = 0 ou g = λ, (1−λ)z1 = 0, (1−λ)z2 = 0,
donc z0 = 0 ou g = λ, z1 = 0, z2 = 0.
g
∗
Donc T = {[1, 0, 0]} ∪ {[0, z1 , z2 ]/z1 , z2 ∈ C }.
Remarque.
On suppose que
On notera
remarque que
P = [1, 0, 0]
S∼
= CP1 .
et
S = {[0, z1 , z2 ]/z1 , z2 ∈ C∗ }.
On
Proposition 77. Soient g = eiθ ∈ G\{−1, 1} et N g le bré normal au-dessus
de
T g.
Alors
g∗
agit sur
Ng
par une rotation d'angle
79
−θ.
Démonstration.
locales
On utilise la carte
φ([z0 , z1 , z2 ]) =
On note
τg
z 1 z2
,
z0 z0
U = {[z0 , z1 , z2 ]/z0 6= 0}
de coordonnées
.
le diéomorphisme induit par
g
sur
T,
φ ◦ τg ◦ φ−1 = φ(τg ([1, x1 , x2 ]))
= φ([eiθ , x1 , x2 ])
= (e−iθ x1 , e−iθ x2 )
alors
−iθ
e
0
mat(τg,∗[1,x−1,x−2] ) =
.
0
e−iθ
D'où le résultat.
Rappel. La cohomologie de de Rham de CP2 est donnée par :
H 0 (CP2 ) = C1, H 1 (CP2 ) = {0}, H 2 (CP2 ) = Cω, H 3 (CP2 ) = {0},
H 4 (CP2 ) = Cω ∧ ω où ω est une classe caractéristique.
Proposition 78.
La signature basique de
G
σ(M, F) = ind(D+
)=
(M, F)
Z Z
L(g)
G
et
Z
est donnée par :
Mg
Z
σ(M, F) =
L(g, P ) +
L(g, S)dg
S
G
Z
où
L(g, P )
L(g, S)
et
se calculent par la formule d'Atiyah-Singer.
S
Démonstration.
la
Il sut d'appliquer la formule d'Atiyah-Segal-Singer pour
G-signature.
Proposition 79.
Démonstration.
Si
g = eiθ
Comme
on a,
{P }
θ
L(g, P ) = −cotan2 ( ).
2
est une variété de dimension 0,
en appliquant la formule d'Atiyah-Segal-Singer on a
c'est-à-dire
Z
Si
Z
L(g, S) =
où
c1 (N g )
−θ −2
i tan( )
,
2
θ
L(g, P ) = −cotan2 ( ).
2
Proposition 80.
S
L(g, P ) =
20
g = eiθ ,
on a
2
(1 + cotan
S
θ
θ
( ))c1 (N g ) = 1 + cotan2 ( )
2
2
est la première classe de Chern de
80
N g.
Z
S
c1 (N g )
Démonstration.
On applique la formule d'Atiyah-Segal-Singer pour la
G-
signature.
N g = N g (θ), t = 1, r = 0 et s(θ) = 1.
Z
Z −θ −1
Donc
L(g, S) = 2
i tan( )
L(M g )mθ (N g ).
2
S
S
g
g
g
4k
On a L(M ) = 1 + L1 (M ) + ... où Lk (M ) ∈ H (S).
k
Or dimC S = 1, donc H (S) = {0}, ∀k ≥ 3.
Z
Z
θ
g
mθ (N g ).
L(g, S) = 2icotan
Donc L(M ) = 1 et
2
S
S
θ
g
g
g
2
Calculons m (N ). On note y = c1 (N ) et on rappelle que c1 (N ) ∈ H (S).
−iθ
y
−iθ 1 + th( 2 )th( 2 )
θ
g
2
On a m (N ) = th(
)
et th(z) = z + o(z ),
y
−iθ
2
th( ) + th(
)
2
2
−iθ y
−iθ y
1 + th(
)
1 + th(
)
−iθ
2 2 =
2 2 .
θ
g
)
donc m (N ) = th(
−iθ
−iθ y
y
2
+ th(
)
coth(
) +1
2
2
2 2
−iθ y
−iθ y
1
= 1 − z + o(z 2 ), donc mθ (N g ) = (1 + th(
) )(1 − coth(
) ).
Or
1+z
2 2
2 2
i
θ
θ
θ
g
Or th(iz) = i tan z , donc m (N ) = 1 − (tan
+ cotan )y . Donc on a
2
2
2
Z
Z
θ
L(g, S) = 2icotan( ) mθ (N g )
2 S
S
Z
i
θ
θ
θ
(tan( ) + cotan( ))y
= −2icotan( )
2 S2
2
2
Z
θ
= (1 + cotan2 ( ))c1 (N g )
2
S
Ici
Corollaire 10.
La signature basique de
(M, F)
est donnée par
G
σ(M/F) = ind(D+
) = 1.
Démonstration.
G
ind(D+ )
Z
Or
2
cotan
S1
En raison des résultats précédents, on a
Z
2
−cotan
=
S1
θ dθ
est
( )
2 2π Z
Donc on a forcément
G
divergente et ind(D+ )
c1 (N g ) = 1
S
Remarque.
θ
θ
( ) + (1 + cotan2 ( ))
2
2
G
G
c1 (N g )
S
dθ
.
2π
∈ Z.
et ind(D+ )
= 1.
On peut retrouver ce résultat par une autre méthode :
G
on a déjà vu que ind(D+ )
groupe
Z
est connexe,
= σ(T /G) (voir corollaire 3 page
donc σ(T /G) = σ(T ) = σ(CP2 ) = 1.
81
26), or ici le
Remarque.
Z Z
G
On a ind(D+ )
L(g)dg .
=
En eet :
G TG
¯
<g>
g ∈ G, on a T g = T <g> = T
,
¯ > son adhérence.
où < g > est le sous-groupe engendré par g et < g
2πiθ
Si θ ∈]0, 1[ est irrationnel, alors < e
> est dense dans G.
2πiθ > et A = ∪
On note Aθ =< e
θ∈]0,1[,θ∈Q
/ Aθ .
c
On remarque que le complémentaire A est dénombrable. On a
Z Z
G
L(g)dg
ind(D+ ) =
g
Z Z
ZG ZT
L(g)dg
L(g)dg +
=
g
Ac M g
ZA ZT
L(g)dg car Ac est de mesure nulle
=
G
ZA ZT
Z Z
=
L(g)dg +
L(g)dg
G
c MG
A
T
A
Z Z
=
L(g)dg.
Si
TG
G
Pourtant il n'est pas possible d'intervertir ces deux intégrales. En eet :
Z
Z
Z
Z
L(g)dg =
TG
TG
G
Z
2
mais
cotan
S1
Exemple 13.
θ
( )
2
θ
θ
dθ
−cotan2 ( ) + (1 + cotan2 ( ))c1 (N g ) ,
2
2
2π
S1
est divergente.
On considère le feuilletage par suspension où
B = S 1 , T = CP2 .
B est alors Z, on dénit le
h : Z → Z3 = {0, 1, 2} par 1 7→ 1 où 1 agit sur T par
Le groupe fondamental de
morphisme de groupe
1.[z0 , z1 , z2 ] = [z1 , z2 , z0 ].
On note
G = Z3 = h(π1 (B)).
aux formes
j=e
G
D+
sur
G-invariantes.
Proposition 81.
i 2π
3
(M, F) se
T restreint
Le calcul de la signature basique de
ramène au calcul de l'indice de l'opérateur de signature
On note
, alors la variété de
A0 = [1, 1, 1], A1 = [1, j, j 2 ], A2 = [1, j 2 , j] où
1
points xes associée à 1 est : T = {A0 , A1 , A2 }.
Démonstration.
On suppose que 1.[z0 , z1 , z2 ] = [z0 , z1 z2 ].
z1 = λz0 , z2 = λz1 , z0 = λz2 où λ ∈ C∗ ,
2
3
2
3
donc z1 = λz0 , z2 = λ z0 , z0 = λ z0 et z1 = λz0 , z2 = λ z0 , λ = 1.
2
2
Donc les points xes de 1 sont de la forme [z0 , λz0 , λ z0 ] = [1, λ, λ ]
où λ est une racine cubique de l'unité. D'où le résultat.
Donc
Remarque. Comme 1 est un générateur de G on a T G = T 1 = {A0 , A1 , A2 }.
82
Proposition 82. On utilise la carte U = {[z0 , z1 , z2 ]/z0 6= 0} de coordonnées
locales
φ([z0 , z1 , z2 ]) = (
On note
alors
g=1
et
τg
z1 z2
, ).
z0 z0
le diéomorphisme induit sur
 x
2
−
 x21
mat(τg,∗[1,x−1,x−2] ) =  1
− 2
x1
Démonstration.
T,
1
x1 
.
0
On a :
φ ◦ τg ◦ φ−1 = φ(τg ([1, x1 , x2 ]))
= φ([x1 , x2 , 1])
x2 1
,
,
=
x1 x1
d'où le résultat.
Proposition 83.
La signature basique de
G
σ(M/F) = ind(D+
)=
(M, F)
Z Z
L(g)
G
et
Z
où
est alors donnée par :
Mg
Z
Z
Z
1
1
L(0, M ) +
L(1, M ) +
L(2, M 2 ))
σ(M/F) = (
3 M
M1
M2
Z
Z
1
L(0, M ) = σ(M ) = 1 et
L(1, M ) et
L(2, M 2 ) se calculent
M1
M
M2
par la formule
d'Atiyah-Segal-Singer.
Z
L(1, M 1 ) = L(1, A0 ) + L(1, A1 ) + L(1, A2 )
De plus
Z
et
M1
2
L(2, M ) = L(2, A0 ) + L(2, A1 ) + L(2, A2 ).
M2
Démonstration.
C'est la formule d'Atiyah-Segal-Singer pour la
Proposition 84.
Démonstration.
On a
Soit
N
L(1, Ak ) = L(2, Ak ) =
l'espace tangent à
M
1
.
3
en
Ak , N
est un espace vecto-
riel complexe de dimension complexe 2.

−1
−1 1

On a : mat(τ1,∗A0 ) =
, mat(τ1,∗A1 ) =  1
−1 0
− 2
j


1
−1

j 2 .
et mat(τg,∗A2 ) = 

1
−
0
j
83
G-signature.

1
j 2 ,

0
tr(mat(τ1,∗Ak )) = −1 et det(mat(τ1,∗Ak )) = 1.
mat(τ1,∗Ak ) sont donc les racines du polynôme
2
X + X + 1, c'est-à-dire les racines cubiques de l'unité : j, j 2 .
2
De même les valeurs propres de mat(τ2,∗Ak ) sont j et j .
θ −1
0
D'après Atiyah-Segal-Singer on en déduit que L(1, Ak ) = 2 (i tan( ))
(i tan(θ))−1
2
2π
.
où θ =
3
1
1
Donc L(1, Ak ) =
. De même L(2, Ak ) =
.
3
3
Donc
Les valeurs propres de
Remarque.
On remarque que
G
préserve l'orientation.
Corollaire 11. La signature basique de (M, F) est donnée par σ(M/F) = 1.
Démonstration.
Z
L(1, Ak ) = L(2, Ak ) =
L(1, M 1 ) = L(1, A0 ) + L(1, A1 ) + L(1, A2 )
or
Z
On a vu que
1
,
3
et
M1
L(2, M 2 ) = L(2, A0 ) + L(2, A1 ) + L(2, A2 ).
Z
Z
1 1 1
1
L(2, M 2 ) = 1.
Donc
L(1, M ) = + + = 1 et de même
3 3 3Z
M1
Z
Z M2
1
Or σ(M/F) =
(
L(0, M ) +
L(1, M 1 ) +
L(2, M 2 )),
3 M
1
2
M
M
1
donc σ(M/F) =
(1 + 1 + 1) = 1.
3
M2
Remarque.
Ici on a
σ(M/F) = 1 = σ(T ).
On peut retrouver ce résultat par une autre méthode :
2 (T ) = C et H 2 (T ) = {0} on a H 2 (T )G = C
H+
−
+
2 (T )G − dim H 2 (T )G = 1.
σ(M/F) = dim H+
−
comme
Donc
Exemple 14.
On note
et
2 (T )G = {0}.
H−
H comme
a b
l'ensemble des matrices de M2 (C) de la forme
, où a et b vérient
−b̄ ā
|a|2 + |b|2 = 1. On note G = SU (2). Le groupe G est isomorphe à
{q ∈ H/|q| = 1}. On considère le feuilletage par suspension B×T où T = HP1
et G = SU (2) agit sur T par
H
le corps des quaternions. On peut voir
g.[q0 , q1 ] = [g.q0 , q1 ].
Le calcul de la signature basique se ramène au calcul de l'indice de l'opérateur
de signature sur
T
Proposition 85.
restreint aux formes
On note
G.
G-invariantes D+
A0 = [0, 1] et A1 = [1, 0]. Soit g ∈ G\{1},
g est M g = {A0 } ∪ {A1 }. On a donc
alors la variété de points xes de
M G = {A0 } ∪ {A1 }.
84
Démonstration.
Donc
Donc
Donc
Donc
On suppose que g.[q0 , q1 ] = [q0 , q1 ].
gq0 = λq0 , q1 = λq1 où λ ∈ C∗ .
(g − λ)q0 = 0, (1 − λ)q1 = 0.
g = λ, q1 = 0 ou q0 = 0, λ = 1.
les points xes sont [q0 , 0] et [0, q1 ], c'est-à-dire [0, 1]
Rappel.
Soit
G
un groupe de Lie compact connexe et
−1 )
fonction continue qui vérie f (gtg
Z
f (g)dg =
G
où
W
1
|W |
Z
= f (t),
[1, 0].
et
f : G → C
une
alors
det((I − Ad(g −1 )|g/t )f (t)dt
T
G, T
désigne le groupe de Weyl de
le tore maximal de
G,
et
g, t
leur
algèbre de Lie respective.
Démonstration.
Voir [Far06] par exemple.
Rappel.
Le tore de SU (2) est l'ensemble des matrices de M2 (C) de la forme
eiθ
0
−iθ
0 e
. Donc le tore de
Le groupe de Weyl de
Démonstration.
SU (2)
SU (2)
est isomorphe à
S1.
est le groupe des permutations
S2 .
Voir [Far06] par exemple.
Proposition 86.
La signature basique de
1
σ(M/F) =
2
Z
est alors donnée par
Z
L(g)φ(g)dg
S1
φ(g) = det(I −Ad(g −1 )|su(2)/s1 ), s1
désigne l'algèbre de Lie de SU (2).
où
(M, F)
Mg
désigne l'algèbre de Lie de
S1
et
su(2)
En particulier
σ(M/F) =
où
L(g, A0 )
et
L(g, A1 )
Démonstration.
1
2
Z
(L(g, A0 ) + L(g, A1 ))φ(g)dg
S1
se calculent par la formule d'Atiyah-Segal-Singer.
Par la formule d'Atiyah-Segal-Singer pour la
a
Z
Z
L(g)dg =
σ(M/F) =
SU (2)
où
D
Z
Mg
ind
G
G-signature on
(D)(g)dg
SU (2)
T.
(D)(g) = χV (g) − χV 0 (g) où χV (g) est le caractère de la représentaker D et χV 0 (g) est le caractère de la représentation ker D∗ .
désigne l'opérateur de signature sur
G
Or ind
tion
Comme le caractère d'une représentation est une fonction centrale on a que
ind
G
(D)
g
vérie ind
(D)(tgt−1 ) = indG (D)(g).
85
G
(D).
Donc on peut appliquer la formule de Weyl à ind
Comme
W = S2 ,
on a
Z
1
σ(M/F) =
|W |
Proposition 87.
φ(g)ind
G
S1
Soit
g∈
1
(D)(g)dg =
2
Z
Z
φ(g)L(g)dg.
S1
Mg
iθ
e
0
g sous la forme g =
,
0 e−iθ
iθ
e
0
, où τg est
mat(τg,∗A1 ) =
0 e−iθ
S 1 , on écrit
e−iθ
0
et
alors mat(τg,∗A0 ) =
0
e−iθ
le diéomorphisme sur T induit par g .
Démonstration.
On écrit [1, q] sous la forme [1, 0, α, β], α, β ∈ C.
g([1, 0, z1 , z2 ]) = [eiθ , 0, z1 , z2 ] = [1, 0, e−iθ z1 , e−iθ z2 ].
Or l'application [1, 0, z1 , z2 ] 7→ (z1 , z2 ) est une carte de T ,
−iθ
e
0
donc mat(τg,∗A0 ) =
.
0
e−iθ
iθ
e
0
iθ
−iθ
On a g([z1 , z2 , 1, 0]) = [e z1 , e
z2 , 1, 0], donc mat(τg,∗A1 ) =
.
0 e−iθ
On a
Remarque.
On remarque
Proposition 88.
Soit
G
préserve l'orientation.
g ∈ S 1 \{1},
on a
θ
L(g, A1 ) = −cotan2 ( ).
2
Démonstration.
θ
L(g, A0 ) = cotan2 ( )
2
et
On applique la formule d'Atiyah-Segal-Singer pour la
G-
−θ
−θ 2
0
signature, L(g, A0 ) = 2
i tan( ) = −cotan2 ( ).
2
2
θ
−θ
θ
0
−1 (i tan(
Et L(g, A1 ) = 2 (i tan( ))
))−1 = cotan2 ( ).
2
2
2
Corollaire 12. La signature basique de (M, F) est donnée par σ(M/F) = 0.
Démonstration.
On a
G
σ(M/F) = ind(D+
)=
et
1
2
L(g, A0 ) + L(g, A1 ) = −cotan2 (
Donc
σ(M/F) = 0.
Remarque.
Ici on a
Z
(L(g, A0 ) + L(g, A1 ))φ(g)dg,
S1
−θ
θ
) + cotan2 ( ).
2
2
σ(M/F) = 0 = σ(T ).
On peut retrouver ce résultat par une autre méthode :
2 (T ) = {0} et H 2 (T ) = {0},
HP1 ∼
= S 4 on a H+
−
2
G
2
G
donc H+ (T ) = {0} et H− (T ) = {0}.
2
G
2
G
Donc σ(M/F) = dim H+ (T ) − dim H− (T ) = 0.
comme
86
4.7.2 Exemples de calculs d'indice de l'opérateur de Dolbeault basique
Exemple 15.
On considère le feuilletage par suspension où
B = S 1 , T = CP2 .
Le groupe fondamental de
morphisme de groupe
h : Z → Z3 = {0, 1, 2}
B est alors Z, on dénit le
1 7→ 1 où 1 agit sur T par
par
1.[z0 , z1 , z2 ] = [z1 , z2 , z0 ].
On note
G = Z3
et on reprend les notations de l'exemple 13.
Comme dans le cas de l'opérateur de signature basique, l'opérateur de Dolbeault basique
Dol
DB
est conjugué à l'opérateur de Dolbeault sur
Dol .
G-invariantes DG
Dol
de indB (DB ) se ramène
T
restreint
aux formes
Le calcul
donc au calcul de l'indice de
Dol .
DG
On appliquera donc la formule de Lefschetz holomorphe (théorème 9 page
28) et on prendra ici pour bré vectoriel le bré trivial
On notera ind
G
E = T × C.
(DDol )(g) = Dol(g, T g ).
Proposition 89.
L'indice de l'opérateur de Dolbeault basique est donné
par :
Dol
indB (DB )
Z
où
1
=
3
Z
Z
Dol(0, M ) +
Dol(2, M ) ,
Z
1
2
Dol(1, M ) +
M1
M
M2
Z
Dol(0, M ) = ind(DDol ) = χ(T, E) et
Dol(1, M 1 ) et
Z
M1
M
Dol(2, M 2 )
M2
se calculent par la formule de Lefschetz holomorphe.
Z
1
Dol(1, M ) =
De plus
M1
Démonstration.
2
X
Z
2
Dol(1, Ak ) et
Dol(2, M ) =
M2
k=0
Dol )
On sait que indB (DB
2
X
Dol(2, Ak ).
k=0
Dol ),
= ind(DG
il sut alors d'appliquer le théorème de Lefschetz holomorphe.
Le calcul des points xes a été fait précédemment (voir proposition 81 page
81).
Proposition 90.
Démonstration.
On a
Dol(1, Ak ) =
La variété
{Ak }
1
3
et
Dol(2, Ak ) =
est de dimension 0, donc selon la formule
de Lefschetz holomorphe on a
Dol(1, Ak ) =
1
det(1 − g|(N g )∗ )
= ((1 − ei
= (1 − ei
1
=
3
De même
Dol(2, Ak ) =
1
.
3
1
.
3
87
2π
3
4π
3
)(1 − ei
− ei
2π
3
4π
3
))−1
+ 1)−1
Proposition 91.
L'indice de l'opérateur de Dolbeault basique est donné
par :
Dol
indB (DB
Démonstration.
3indB (∆00B )
Au vue des résultats précédents on a :
= χ(T, E) + 3 ×
Exemple 16.
1
2
) = χ(T, E) + .
3
3
1
1
+3× .
3
3
On considère le feuilletage par suspension où
B = S 1 , T = CP3 .
Le groupe fondamental de
morphisme de groupe
h : Z → Z4 = {0, 1, 2, 3}
B
est alors
Z,
on dénit le
1 7→ 1
où
1
par
agit sur
T
par
1.[z0 , z1 , z2 , z3 ] = [z1 , z2 , z3 , z0 ].
On note
G = Z4 .
Pour calculer l'indice de l'opérateur de Dolbeault basique,
on se ramène au calcul de l'indice de l'opérateur de Dolbeault sur
aux formes
T
restreint
Dol .
G-invariantes DG
On appliquera donc la formule de Lefschetz holomorphe et on prendra ici
pour bré vectoriel le bré trivial
E = T × C.
π
iθ
3iθ ],
et A0 = [1, 1, 1, 1], A1 = [1, e , −1, e
2
A2 = [1, −1, 1, −1], A3 = [1, e3iθ , −1, eiθ ].
1
Alors la variété de points xes associée à 1 est : T = {A0 , A1 , A2 , A3 }.
Proposition 92.
Démonstration.
On note
θ=
La démonstration est similaire à la démonstration de la pro-
position 81 page 81.
Remarque.
Comme 1 engendre
Proposition 93.
G
on a
T G = T 1 = {A0 , A1 , A2 , A3 }.
La variété de points xes associée à 2 est
T 2 = F1 ∪ F2
où
F1 = {[z1 , z2 , z1 , z2 ]/(z1 , z2 ) 6= (0, 0)} et
F2 = {[z1 , −z2 , −z1 , z2 ]/(z1 , z2 ) 6= (0, 0)}.
Démonstration.
2.[z0 , z1 , z2 , z3 ] = [z0 , z1 , z2 , z3 ].
∗
Donc z2 = λz0 , z3 = λz1 , z0 = λz2 , z1 = λz3 où λ ∈ C ,
2
2
et z2 = λz0 , z3 = λ z3 , z0 = λ z0 , z1 = λz3 ,
2
donc z0 6= 0, λ = 1, z2 = λz0 , z1 = λz3
2
ou bien z0 = 0, z2 = 0, λ = 1, z1 = λz3 .
Donc [z0 , z1 , z2 , z3 ] est de la forme [z0 , z1 , λz0 , λz1 ] avec (z0 , z1 ) 6= (0, 0)
λ2 = 1.
On suppose que
et
D'où le résultat.
Remarque.
(ii) On a
H = Z2 , le
T H = T 2.
F2 ∼
= CP1 .
(i) On note
est isomorphe à
H,
F1 ∼
= CP1
donc
et
88
sous-groupe de
G
engendré par 2
Proposition 94. On note C = τ1,∗Ak , alors le spectre de C est {−1, eiθ , e3iθ }.
De même le spectre de
Démonstration.
λ4
On a
τ3,∗Ak
est
X4 − 1
{−1, eiθ , e3iθ }.
C.
annule
λ
Si
est valeur propre de
C,
alors
= 1.
iθ 3iθ }.
C
, donc σ(C) ⊂ {−1, e , e

−1 −i 0
0 −i.
Après calcul on a, mat(τ1,∗A1 ) =  −i
1
0
0
Donc tr(mat(τ1,∗A1 )) = −1 et det(mat(τ1,∗A1 )) = −1.
iθ 3iθ } (si une valeur propre avait une multiplicité
Donc σ(τ1,∗A1 ) = {−1, e , e
≥ 2, on trouverait une autre valeur
 pour la traceet le déterminant).
−1 −1 0
0 −1.
Après calcul on a, mat(τ1,∗A1 ) =  1
−1 0
0
Donc tr(mat(τ1,∗A1 )) = −1 et det(mat(τ1,∗A1 )) = −1.
iθ 3iθ }.
Donc σ(τ1,∗A1 ) = {−1, e , e


−1 i 0
0 i .
Après calcul on a, mat(τ1,∗A1 ) =  i
1 0 0
Donc tr(mat(τ1,∗A1 )) = −1 et det(mat(τ1,∗A1 )) = −1.
iθ 3iθ }.
Donc σ(τ1,∗A1 ) = {−1, e , e
Or 1 n'est pas valeur propre de
Proposition 95.
L'indice de l'opérateur de Dolbeault basique est donné
par :
Dol
indB (DB
1
=
4
Z
Z
Z
1
Dol(0, M ) +
Z
2
Dol(1, M ) +
M1
M
Dol(2, M ) +
M2
Dol(0, M ) = ind(DDol ) = χ(T, E) et
où
et
Z
)
Z
Z
M3
Dol(1, M 1 ),
M1
M
Dol(3, M )
3
Z
Dol(2, M 2 )
M2
Dol(3, M 3 ) se calculent par la formule de Lefschetz holomorphe.
Z
Z
3
3
X
X
1
Dol(3, Ak )
De plus
Dol(1, M ) =
Dol(1, Ak ),
Dol(3, M 3 ) =
M3
M1
et
Z
Dol(1, M 2 ) =
M2
Démonstration.
M3
k=0
Z
k=0
Z
Dol(2, F1 ) +
F1
Dol(2, F2 ).
F2
Dol )
On sait que indB (DB
Dol ),
= ind(DG
il sut alors d'appliquer le théorème de Lefschetz holomorphe.
Le calcul des points xes a été fait précédemment.
Proposition 96.
On a
Dol(1, Ak ) =
1
4
89
et
Dol(3, Ak ) =
1
.
4
Démonstration.
La variété
{Ak }
est de dimension 0, donc selon la formule
de Lefschetz holomorphe on a
Dol(1, Ak ) =
1
det(1 − g|(N g )∗ )
= ((1 + 1)(1 − eiθ )(1 − e3iθ ))−1
où
θ=
2π
4
1
= (1 + i − i + 1)−1
2
1
=
4
De même
Dol(3, Ak ) =
Proposition 97.
Démonstration.
On note
N
1
.
4
Z
Dol(2, F1 ) = −
On a
F1
Z
Dol(2, F2 ) = −
et
F2
1
.
4
On applique la formule de Lefschetz holomorphe.
le bré normal à
Le polynôme
1
4
X2 − 1
annule
F1 .
τ2,∗ ,
donc le spectre de
{−1, 1}, et la seule valeur propre de τ2,∗ agissant
Donc det(1 − τ2,∗ )|N = (1 + 1)(1 + 1) = 4.
Le bré E est trivial, donc ch(E|F1 ) = 1.
Z
Z
U −1 (N )td(F1 )
Donc
Dol(2, F1 ) =
.
4
F1
F1
k
Or F1 = CP1 et H (CP1 ) = {0} si k ≥ 3.
sur
τ2,∗ est contenu
N est -1.
dans
1
td(F1 ) = td(CP1 ) = 1 + T d1 (CP1 ) = 1 + c1 (CP1 ).
2
On notera ηk le bré tautologique au-dessus de CPk ,
on a c1 (T CP1 ) = −2c1 (η1 ) (voir [MS74]). Donc td(CP1 ) = 1 − c1 (η1 ).
∗
Or (T CP3 )|CP1 = T CP1 ⊕ N , donc i (T CP3 ) = T CP1 ⊕ N où i : CP1 → CP3
Par dénition
est l'inclusion.
U −1 (i∗ (T CP3 )) = U −1 (T CP1 )U −1 (N ),
−1 (N ) = (U −1 (T CP ))−1 i∗ (U −1 (T CP )).
et par conséquent U
1
3
Or T CP1 est un bré en droites complexes au-dessus de CP1 ,
Donc
U
−1
(T CP1 ) = =
1 − e−x1 −iπ
1 − e−iπ
= 2(1 + e−x1 )−1
= 2(2 − x1 )−1
1
= (1 − x1 )−1
2
1
= 1 + x1
2
90
donc
−1
où
x1 = c1 (T CP1 )
1
(U −1 (T CP1 ))−1 = 1 − x1 .
2
−1 (T CP ).
Calculons U
3
Rappelons qu'on a T CP3 ⊕ η3 ∼
= η3∗ ⊕ ... ⊕ η3∗
−1
−1
∗
4
Donc U
(T CP3 ) = (U (η3 )) (U −1 (η3 ))−1 .
Donc
(voir [MS74]).
Par un calcul similaire au calcul précédent on a
De plus
1
(U −1 (η3 ))−1 = 1 − c1 (η3 ).
2
∗
1 − e−c1 (η3 )−iθ −1
)
1 − e−iθ
= 2(1 + ec1 (η3 ) )−1
U −1 (η3∗ ) = (
= 2(2 + c1 (η3 ))−1
1
= (1 + c1 (η3 ))−1
2
1
= 1 − c1 (η3 )
2
Donc
Donc
1
4
(U −1 (η3∗ ))4 = (1 − c1 (η3 ))4 = 1 − c1 (η3 ) = 1 − 2c1 (η3 ).
2
2
1
U −1 (T CP3 ) = (1 − 2c1 (η3 ))(1 − c1 (η3 ))
2
1
= 1 − c1 (η3 ) − 2c1 (η3 )
2
5
= 1 − c1 (η3 )
2
Donc
Donc
5
i∗ (U −1 (T CP3 )) = 1 − c1 (η1 ).
2
5
U −1 (N ) = (1 + 2c1 (η1 ))(1 − c1 (η1 ))
2
5
= 1 + 2c1 (η1 ) − c1 (η1 )
2
1
= 1 − c1 (η1 )
2
Donc
1
U −1 (N )td(F1 ) = (1 − c1 (η1 ))(1 − c1 (η1 ))
2
1
= 1 − c1 (η1 ) − c1 (η1 )
2
3
= 1 − c1 (η1 )
2
91
Z
Donc
De même
Z
3
3
− c1 (η1 ) = .
2
8
CP1
3
Dol(2, F2 ) = .
8
F2
1
Dol(2, F1 ) =
4
F1 Z
Proposition 98.
Démonstration.
Dol
indB (DB )
Dol )
On a indB (DB
1
5
= χ(T, E) + .
4
16
Au vu des résultats précédents on a,
1
= (ind(DDol ) + 1/4 + 1/4 + 3/8 + 3/8).
4
92
Chapitre 5
Invariance par homotopie
feuilletée de la signature
basique
Nous allons montrer à l'aide d'un "lemme de Poincaré basique" que la
signature basique est un invariant d'homotopie feuilletée.
Proposition 99.
(N, F 0 ) une variété feuilletée vériant les mêmes
0
∗
∗
0
conditions et f : (M, F) → (N, F ) une application feuilletée, alors f (Ω (N/F ))
∗
est inclus dans Ω (M/F)) et f induit une application linéaire
Soient
f ∗ : (H ∗ (N/F 0 )) → H ∗ (M/F)).
Démonstration.
Soient
Dénition 69.
Soit
ω ∈ Ω∗ (N/F 0 ) et V ∈ Γ(T F),
∗
0
on a iV (f (ω))x = if∗x (Vx ) (ω), ∀x ∈ M , or f∗ (T F) ⊂ (T F ),
0
donc f∗x (Vx ) ∈ Tf (x) F .
∗
0
Or ω ∈ Ω (N/F ), donc if∗x (Vx ) (ω) = 0, ∀x ∈ M .
∗
∗
De même on a iV (df (ω)) = 0, donc f (ω) est basique.
et
t ∈ R,
j : M → R × M , x 7→ (t, x)
Z t1
I01 : Ω∗ (R × M ) → Ω∗ (M ), ω 7→
jt∗ (ω)dt.
on note
0
Proposition 100.
On note π2 : R × M → M la deuxième projection
R × M du feuilletage π2∗ (T F) où π2∗ (T F)(t,x) = Tx F .
I01 (Ω∗ (R × M/π2∗ (T F)) ⊂ Ω∗ (M/F).
et on
munit
On a
Démonstration.
jt : (M, F) → (R × M, π2∗ (T F)) est feuilletée.
Soit x ∈ M et jt∗x : Tx M → T(t,x) R×M , l'application induite par jt . Comme
0
0
T(t,x) R × M = Tt R × Tx M = R × Tx M , et jt∗x est de la forme
,
0 IdTx M
∗
donc Vx ∈ Tx F entraîne que jt∗x (Vx ) ∈ Tx F . Ainsi jt∗ (T F) ⊂ π2 (T F)),
Montrons que
93
jt est feuilletée.
∗
ω ∈ Ω∗ (R × M/π2∗ (T F)), donc jt∗ (ω)
∈Z Ω1 (M/F).
Z 1
iV (jt∗ (ω))dt = 0
jt∗ (ω)dt =
V ∈ Γ(T F), on a iV
c'est-à-dire
Soit
Soit
0
0
jt∗ (ω)est F -basique,
Z
Z 1
∗
iV ◦ d
jt (ω)dt = iV
car
et
1
djt∗ (ω)dt
Z
=
0
0
jt∗ (ω) est F -basique.
1
Donc I0 (ω) est F -basique.
1
iV ◦ d(jt∗ (ω))dt = 0
0
car
Proposition 101. Si ω ∈ Ω∗ (R×M ), on a j1∗ (ω) − j0∗ (ω) =
Démonstration.
que
Z
1
js∗ L d (ω) ds.
dt
0
ω ∈ Ωk (R × M ), par linéarité on peut supposer
ω = f (t, x)dxi1 ∧ ... ∧ dxik + g(t, x)dt ∧ dxi1 ∧ ... ∧ dxik−1 . On a
Si
alors
js∗ (L d (f (t, x)dxi1 ∧ ... ∧ dxik ))
dt
d
∗
f (t, x)dxi1 ∧ ... ∧ dxik + L d (dxi1 ∧ ... ∧ dxik )
= js
dt
dt
d
f (t, x)dxi1 ∧ ... ∧ dxik .
=
dt |s
Or
L d (g(t, x)dt ∧ dxi1 ∧ ... ∧ dxik−1 )
est une forme de bidegré
(1, k − 1),
dt
c'est-à-dire
L d (g(t, x)dt ∧ dxi1 ∧ ... ∧ dxik−1 ) ∈
Ω(1,k−1) (R
× M ),
dt
∗
ainsi js (L d (g(t, x)dt ∧ dxi1 ∧ ... ∧ dxik−1 )) ∈
dt
∗
d'où js (L d (g(t, x)dt ∧ dxi1 ∧ ... ∧ dxik−1 )) =
Ω(1,k−1) (M )
= {0},
0.
dt
Par conséquent
Z
0
1
js∗ (L
Z
d
dt
1
d
f (t, x)dxi1 ∧ ... ∧ dxik ds
0 dt |s
= f (1, x)dxi1 ∧ ... ∧ dxik − f (0, x)dxi1 ∧ ... ∧ dxik
(ω))ds =
= j1∗ (ω) − j0∗ (ω).
Proposition 102.
(N, F 0 ) une variété feuilleté vériant les mêmes
hypothèses que (M, F) et φ, ψ : M → N des applications feuilletées homo∞ telle
topes, c'est-à-dire qu'il existe H : R × M → N une application C
Soient
que
H(0, x) = φ(x)
(ii) H(1, x) = ψ(x)
(iii) ∀t ∈ R, H(t, .) est
(i)
feuilletée.
94
h : Ω∗ (N ) → Ω∗ (M )
h(Ω∗ (N/F 0 )) ⊂ Ω∗ (M/F).
Alors l'application
Démonstration.
dénie par
h = I01 ◦ i d ◦ H ∗
vérie
dt
H : (R×M, π2∗ (T F)) → (N, F 0 ) est feuilletée.
∗
0
Soit (t, x) ∈ R × M , montrons que H∗(t,x) (π2 (T F)(t,x) ) ⊂ TH(t,x) F ,
0
c'est-à-dire H∗(t,x) (Tx F) ⊂ TH(t,x) F .
0
Comme ∀t ∈ R, H(t, .) est feuilletée, d'où ∀t ∈ R, H(t, .)∗x (Tx F) ⊂ TH(t,x) F ,
0
donc H∗(t,x) (Tx F) ⊂ TH(t,x) F et H est feuilletée.
∗
0
∗
∗
Soit ω ∈ Ω (N/F ), donc H (ω) ∈ Ω(R × M/π2 (T F)).
∗
∗
Montrons que i d (H (ω)) ∈ Ω(R × M/π2 (T F)).
dt
∗
Soit Y ∈ Γ(π2 (T F)),
∗
∗
∗
∗
on a iY ◦ i d (H (ω)) = −i d ◦ iY (H (ω)) = 0 car H (ω) est π2 (T F)-basique.
Montrons que
dt
dt
Et
iY ◦ d ◦ i d (H ∗ (ω)) = iY ◦ (L d − i d ◦ d)(H ∗ (ω))
dt
dt
dt
∗
= iY (L d (H (ω))) − iY ◦ i d (d(H ∗ (ω))
dt
dt
∗
= (L d ◦ iY − i[ d ,Y ] )(H (ω)) + i d ◦ iY (dH ∗ (ω))
dt
dt
dt
= −i[ d ,Y ] (H ∗ (ω))
dt
∗
∗
car H (ω) est π2 (T F)-basique.
∗
∗
Or Y ∈ Γ(π2 (T F)), donc ∀(t, x) ∈ R × M, Y(t,x) ∈ π2 (T F)(t,x) = Tx F et
d
∗
∀t ∈ R, Y(t,x) ∈ Tx F . Donc [ dt , Y ] = 0 et i d (H (ω)) est π2∗ (T F)-basique.
dt
1
Or I0 préserve les formes basiques, donc h(ω) est F -basique.
Proposition 103.
Démonstration.
On a
Sous les mêmes hypothèses, on a
φ∗ − ψ ∗ = h ◦ d + d ◦ h.
ω ∈ Ω∗ (R × M ),
Z 1
∗
∗
j1 (H (ω)) − j0 (H (ω)) =
jt∗ (L d (H ∗ ω))dt, ψ = j1 ◦ H ∗
φ = j0 ◦
∗
Soit
∗
Z
et
dt
0
H ∗ , donc
1
jt∗ ◦ i d ◦ d(H ∗ ω) + jt∗ ◦ d ◦ i d (H ∗ ω)dt
dt
dt
Z 1
Z 1
=
jt∗ ◦ i d ◦ H ∗ (dω)dt +
d ◦ jt∗ ◦ i d (H ∗ ω)dt
ψ (ω) − φ (ω) =
0
0
dt
0
dt
= h ◦ d(ω) + d ◦ h(ω).
Corollaire 13. Sous les mêmes hypotheses, on a φ∗ = ψ∗ sur H ∗ (N/F 0 ).
Proposition 104. Soit f : (M, F) → (N, F 0 ) une équivalence d'homotopie
feuilletée, c'est-à-dire :
95
(i) f est feuilletée
g : (N, F 0 ) → (M, F) une application feuilletée telle
f ◦ g ∼ IdN et g ◦ f ∼ IdM parmi les applications feuilletées.
∗
∗
0
∗
Alors f induit un isomorphisme f : H (N/F ) → H (M/F).
(ii) il existe
Démonstration.
que
H ∗ (M/F) on a g ∗ ◦ f ∗ = Id,
∗
0
∗
∗
et sur H (N/F ) on a f ◦ g = Id,
∗
∗
0
∗
donc f : H (N/F ) → H (M/F) est un isomorphisme.
Sur
On suppose désormais que
et
F
est homologiquement orientable
q = 4l.
Dénition 70.
On dit que
f
Soit
f : (M, F) → (N, F 0 )
une application feuilletée.
préserve les orientations transverses si
f ∗ ([ν]) = λ[ν 0 ]
avec
λ > 0.
Lemme 9.
tée
f : (M, F) → (N, F 0 ) est une équivalence d'homotopie feuille0
q
0
préservant les orientations transverses alors ∀ω ∈ Z (N/F ),
Si
on a
f ∗ (ω 0 ), ν
M
= λ ω0, ν 0 N .
Démonstration. On sait que f induit un isomorphisme
f ∗ : H ∗ (N/F 0 ) → H ∗ (M/F),
∗
0
q
∗
0
donc f ([ν ]) ∈ H (M/F) = R[ν] et f ([ν ]) = λ[ν] avec λ > 0,
∗
0
q−1
ainsi f (ν ) = λν + α où α ∈ dΩ
(M/F).
0
q
0
0
q
0
0
On a ω ∈ Z (N/F ), donc [ω ] ∈ H (N/F ) = R[ν ],
0
0
q−1
0
donc ω = µν + β où µ ∈ R et β ∈ dΩ
(N/F ).
∗ 0
∗ 0
∗
Par conséquent f (ω ) = µf (ν ) + f (β), et
Z
∗ 0 f (ω ), ν M =
(µf ∗ (ν 0 ) + f ∗ (β)) ∧ ∗ν
M
Z
Z
=µ
f ∗ (ν 0 ) ∧ χF +
f ∗ (β) ∧ χF
M
M
Z
f ∗ (β) ∈ dΩq−1 (M/F), donc
f ∗ (β) ∧ χF = 0 (voir proposition 44).
M
Z
Z
Z
∗ 0 (λν
+
α)
∧
χ
=
µλ
ν
∧
χ
+
µ
α ∧ χF .
Ainsi f (ω ), ν
=
µ
F
F
M
M
MZ
M
q−1 (M/F), donc comme précédemment
Or α ∈ dΩ
α ∧ χF = 0
M
Z
∗ 0 et f (ω ), ν
= µλ
dvolM = µλ.
M
M
Z
Z
Z
0 0
0
0
0
0
Or ω , ν
=
(µν + β ) ∧ ∗ν = µ
ν ∧ χF 0 +
β 0 ∧ χF 0 .
N
N
N
N
Z
0
q−1
0
Comme β ∈ dΩ
(N/F ), on a
β ∧ χF 0 = 0.
N
Z
0 0
Donc ω , ν
=µ
dvolN = µ, d'où le résultat.
N
Or
N
96
Théorème 34.
Sous les mêmes hypotheses,
Démonstration.
Soient
QB (f
∗
σ(N/F 0 ) = σ(M/F).
[ω10 ], [ω20 ] ∈ H 2l (N/F 0 ),
[ω10 ], f ∗ [ω20 ])
Z
=
f ∗ (ω10 ∧ ω20 ) ∧ ∗ν
ZM
f ∗ (ω10 ∧ ω20 ) ∧ χF
= f (ω10 ∧ ω20 ), ν M
= λ ω10 ∧ ω20 , ν 0 N
Z
ω10 ∧ ω20 ∧ ∗ν 0
=λ
=
M∗
=
avec
N
λQ0B (ω10 , ω20 )
λ > 0.
σ(Q0B ) = σ(t f ∗ QB f ∗ ) = σ(QB ).
Donc
Exemple 17.
On considère le feuilletage par suspension
B = S 1 , T = CP2 et Γ est isomorphe à Z3 et
Isom(CP2 ) déni par 1.[z0 , z1 , z2 ] = [z1 , z2 , z0 ].
M = B × T /Γ où
Z sur
donné par l'action de
M 0 = B 0 × T 0 /Γ0 où
=
=
Z3 et donné par l'action de Z sur
Isom(CP2 ) déni par 1.(x1 , x2 , x3 , x4 ) = (x2 , x3 , x1 , x4 ).
La signature basique de (M, F) est donnée par σ(M/F) = σ(T /Γ).
2
2
Comme H+ (CP2 ) = R et H− (CP2 ) = 0,
Γ
2
Γ
2
on a H+ (CP2 ) = R et H− (CP2 ) = 0. Donc σ(M/F) = 1.
0
0
0
0
0
0
La signature basique de (M , F ) est donnée par σ(M /F ) = σ(T /Γ ).
2
4
0
0
Comme H (S ) = {0}, on a σ(M /Γ ) = 0.
0
0
On en déduit que les feuilletages (M, F) et (M , F ) ne sont pas homotopi-
On considère également le feuilletage par suspension
B0
S1,
T0
S 4 et
Γ0 est isomorphe à
quement équivalents.
Problème ouvert.
Dans [EKAN93], A. El-Kacimi et M. Nicolau montrent
à l'aide de suites spectrales que la cohomologie basique est un invariant
topologique. Il est surement possible de montrer que la signature basique est
invariante par une homotopie feuilletée continue.
97
Chapitre 6
L'indice basique en tant
qu'indice distributionnel
Dans l'article de 1974 [Ati], Atiyah étudie les opérateurs transversalement
elliptiques par rapport à l'action d'un groupe de Lie compact. Il montre que
de tels opérateurs admettent un indice en tant que distribution. La formule
de N. Berline et M. Vergne permet alors de calculer cet indice ([BGV04,
BV96b, BV96a]). Nous allons reprendre l'article d'Atiyah et l'adapter au cas
d'un feuilletage muni d'une action de groupe de Lie compact respectant le
feuilletage. Nous montrons qu'un opérateur transversalement elliptique par
rapport au feuilletage et à l'action du groupe admet un indice basique en
tant que distribution et étudions certaines propriétés de cet indice. Nous
nissons par explorer le lien avec l'indice distributionnel classique d'Atiyah
sur la variété basique.
6.1 Existence de l'indice distributionnel
Nous considérons toujours notre variété fermée
riemannien. Soit
G
Dénition 71.
On dit qu'une action
est lisse et
c'est-à-dire
M
munie d'un feuilletage
un groupe de Lie compact.
τ : G × M → M est feuilletée si elle
si pour tout g ∈ G, τg = τ (g, .) est une application feuilletée
τg∗ (T F) ⊂ (T F).
Dans la suite on suppose que l'action de
munit
M
G
M est feuilletée et on
G-invariante.
W ] associée à (M, F) vérie
sur
d'une structure riemannienne quasi-brée
On suppose de plus que la variété basique
dim W ] > 0.
Lemme 10.
induite de
G
Soit
E
un
F -bré G-équivariant au-dessus de M . Alors l'action
E , préserve les sections basiques de E .
sur les sections de
98
Démonstration.
∇. Quitte à moyenner
∇ est G-invariante.
Soient σ ∈ Γ(E/F), g ∈ G et V ∈ Γ(T F).
On a ∇V (g.σ) = g.∇V (σ) = 0 puisque σ est basique. D'où le résultat.
On munit
E
d'une connexion basique
cette connexion, on peut supposer que
Notation 12.
E0
des F -brés G-équivariant au-dessus de M et
D : Γ(E/F) →
G-invariant d'ordre
m. On note G l'algèbre de Lie de G. Si Y ∈ G , on note Y ∗ le champ fondamental associé à Y .
∗
Si z ∈ M , on notera Θ(z) l'orbite de z dans M . On note TG M le bré
cotangent à l'action de G sur M déni par :
Soient
E
et
Γ(E 0 /F) un opérateur diérentiel basique
TG∗ M = {ξ ∈ T ∗ M, ξ(Y ∗ ) = 0, ∀Y ∈ G}.
Notons que
TG∗ M
n'est en général ni un bré vectoriel topologique ni une
variété.
Dénition 72.
On dit que D est (G, F)-transversalement elliptique
∀z ∈ M, ∀γ ∈ ((TG∗ M )z ∩ νz∗ F)\{0}, σ(D)(z, γ) est inversible.
Remarque.
On a
Notation 13.
si
(TG∗ M )z ∩ νz∗ F ∼
= (Tz Θ(z) ⊕ Tz F)⊥ .
On notera
H k (G)
le k-ième espace de Sobolev sur
G
qui a
été déni dans la première partie de cette thèse.
D est G-invariant et (G, F)-transversalement elliptique, par
ker D et ker D∗ sont des représentations de G (pas forcément
L'opérateur
conséquent
de dimension nies). On peut alors appliquer le théorème de Peter-Weyl
et écrire le noyau de
D
comme une somme de représentations irréductibles
unitaires :
ker D = ⊕a∈Ĝ ma Va
où
(Va )a∈Ĝ
est un ensemble de représentants des représentations irréduc-
tibles unitaires du groupe
G,
et les entiers
ma
sont les multiplicités qu'on
peut calculer à partir du lemme de Schur.
On pose alors
X
χker D =
ma χa
où
χa
est le caractère de la représentation
a∈Ĝ
Va .
Nous allons voir que cette série est eectivement convergente en un cer-
tain sens. On exprime
χker D
comme une forme linéaire continue sur
C ∞ (G)
dénie par
hχker D , φi :=
X
a∈Ĝ
où
πker D
Z
ma
Z
χa (g)φ(g)dg =:
G
φ(g)tr(πker D (g))dg
G
désigne la représentation de
nous pouvons énoncer :
99
G
dans
ker D.
Avec ces hypothèses,
Théorème 35.]
bolev
χker D
H − dim W (G).
Remarque.
est une distribution qui appartient à l'espace de So-
Par dénition du caractère d'une représentation,
χker D
est une
distribution centrale.
D est
{Y1 , ..., Yk } une base de G et Yi∗ les champs fondaM . On munit E d'une connexion basique ∇ qu'on peut
Nous allons utiliser plusieurs lemmes. Supposons d'abord que
d'ordre
m = 2m0 .
Soient
mentaux induits sur
supposer
G-invariante.
On pose
∆ = Id −
k
X
(∇Yi∗ )2 : Γ(E) → Γ(E).
i=1
Lemme 11.
L'opérateur
Démonstration.
∆
est basique et
G-invariant.
On désigne pour simplier, lorsqu'aucune confusion n'est
∗
possible, par Yi l'opérateur diérentiel associé à
Yi
agissant soit comme
champ de vecteur sur les fonctions diérentiables soit sur les sections diérentiables de
E
via la connexion basique
∇,
i.e. l'opérateur
∗
calcul montre que Yi est un opérateur diérentiel
∇Yi∗ .
Un simple
G-invariant.
∗
Soient V ∈ Γ(T F) et σ ∈ Γ(E/F). Comme ∇ est basique, on a R∇ (V, Yi ) =
0. Donc ∇V (∇Yi∗ (σ)) = −∇Yi∗ (∇V (σ)) − ∇[V,Yi∗ ] (σ).
Comme σ est basique, on a ∇V (σ) = 0. Comme l'action de G sur M est
∗
∗
feuilletée, le champ de vecteurs Yi est feuilleté. Donc [V, Yi ] est tangent au
feuilletage. Ainsi ∇[V,Y ∗ ] (σ) = 0 et ∇V (∇Y ∗ (σ)) = 0.
i
i
∗
∗
Ainsi Yi induit un opérateur Yi : Γ(E/F) → Γ(E/F).
Soient (U, φ) une carte feuilletée de M de coordonnées (x1 , ..., xp , y1 , ..., yq ).
p
q
X
X
∂
∂
∗
∗
gk (x, y)
On peut écrire Yi sous la forme Yi =
fk (x, y)
+
.
∂xk
∂yk
k=1
k=1
yk (exp((tYi ).z) − yk (z)
∗
∗
.
Or Yi (yk ) = fk (x, y) et Yi (yk ) = limt→0
t
L'action de G sur M est feuilletée, donc τexp(tYi ) envoie une feuille sur une
autre feuille et la fonction yk (exp(tYi ).z) est indépendante des coordonnées
xi . Donc fk (x, y) est indépendante de x, et sur Γ(E/F) l'opérateur ∇Yi∗
q
X
s'écrit sous la forme
fk (y)∇ ∂ . C'est-à-dire ∇Yi∗ est un opérateur dié∂yk
k=1
rentiel basique. Donc
Lemme 12.
∆ est un opérateur diérentiel basique G-invariant.
On pose maintenant
0
A = (D, ∆m ) : Γ(E/F) → Γ(E 0 /F) ⊕ Γ(E/F),
A
G-invariant d'ordre m = 2m0 .
∗
injectif si γ ∈ νz F\{0}.
est un opérateur diérentiel basique
Alors le symbole
σ(A)(z, γ)
est
100
Démonstration.
On utilise les notations précédentes et les notations intro-
duites dans la notation 12.
0
σ(A)(z, γ)(η) = (σ(D)(z, γ)(η), σ(∆m )(z, γ)(η)) et
∗
νz F = (νz∗ F ∩ (TG∗ M )z ) ⊕ (νz∗ F ∩ Tz Θ(z)).
∗
∗
∗
On écrit γ = α + ξ où α ∈ νz F ∩ (TG M )z et ξ ∈ νz F ∩ Tz Θ(z),
0
0
m
m
et σ(∆ )(z, γ) = σ(∆ )(z, α).
Supposons que α 6= 0.
m0
On a σ(A)(z, γ)(η) = 0 ⇒ σ(D)(z, γ)(η) = 0 et σ(∆ )(z, γ)(η) = 0.
0
m
Donc η = 0 puisque σ(∆ )(z, γ) est injectif (le symboles de ∆ se calcule
On a
comme dans le cas du laplacien usuel).
α = 0, alors σ(A)(z, γ)(η) = σ(D)(z, γ)(η) = 0,
(G, F)-transversalement elliptique, donc η = 0.
σ(A)(z, γ) est injectif si γ ∈ νz∗ F\{0}.
Si maintenant
or
D
Donc
est
Revenons à présent à la démonstration du théorème 35.
Démonstration du théorème 35.
0
Avec les notations précédentes, l'opérateur
A∗ A = D∗ D + ∆2m : Γ(E/F) → Γ(E/F) est un opérateur diérentiel
0
∗
basique G-invariant d'ordre 4m = 2m. De plus, A A est F -transversalement
elliptique. On note
(ker D)λ = {σ ∈ Γ(E/F)/ D(σ) = 0
et
∆(σ) = λσ}
et
0
(A∗ A)λ = {σ ∈ Γ(E/F)/ A∗ A(σ) = λ2m σ}.
aλ = dim(ker D)λ et bλ = dim(A∗ A)λ .
(ker D)λ ⊂ (A∗ A)λ , donc aλ ≤ bλ < +∞
On pose
On a
(puisque
A∗ A
est
F-
transversalement elliptique).
dim W ]
∗
−s est tras>
, l'opérateur (A A)
4m0
X
bλ
∗
où Sp(A A) désigne le spectre de
2m0 s
λ
∗
Selon le théorème 23 page 60 si
çable et
tr(A∗ A)−s =
λ2m0 ∈Sp(A A)
A∗ A. L'espace
(ker D)λ
est une représentation de dimension nie de
G
et
fλ = χ(ker D)λ son caractère.
G agit unitairement sur (ker D)λ , en diagonalisant g ∈ G, on obtient
|fλ (g)| = |trg|(ker D)λ | ≤ aλ ≤ bλ .
X
fλ
dim W ]
,
h
=
est normalement convergente et h
Donc si s >
0
2m
λm0 s
on note
Comme
λ∈Sp(∆)
est donc une fonction continue.
On note encore
Y1 , ..., Yk les champs de vecteurs
Y1 , ..., Yk ∈ G . On pose
lation à gauche de
∆G = Id −
k
X
i=1
101
Yi2 .
sur
G
prolongés par trans-
∆G (fλ )(g) = tr(∆g|(ker D)λ ).
∗
que Yi (fλ )(g) = tr(Yi g|(KerD) ).
λ
Nous montrons maintenant que
Il sut pour cela de montrer
Soient
σ ∈ (ker D)λ
et
x ∈ M,
alors on a
(Yi∗ ◦ τg )(σ)x = Yi∗ (τg (σ))x
etYi .(τg (σ)e−tYi .x ) − τg (σ)x
t→0
t
tY
i
e .(g.(σ(g−1 e−tYi ).x ) − τg (σ)x
= lim
t→0
t
(etYi g).(σ(g−1 e−tYi ).x ) − τg (σ)x
= lim
t→0
t
τ(etYi g) (σ)x − τg (σ)x
= lim
.
t→0
t
= lim
Par conséquent
Yi∗ ◦ τg = limt→0
tr((Yi∗ ◦ τg )|(ker D)λ ) = limt→0
Or
etYi
τ(etYi g) − τg
t
, et
tr(τ(etYi g)|(ker D)λ ) − tr(τg|(ker D)λ )
t
est la courbe intégrale de
Yi .
.
Donc
e−tYi (fλ )(g) − fλ (g)
t→0
t
fλ (etYi g) − fλ (g)
= lim
t→0
t
tr(τ(etYi g)|(ker D)λ ) − tr(τg|(ker D)λ )
.
= lim
t→0
t
Yi (fλ )(g) = lim
Yi (fλ )(g) = tr(Yi∗ g|(KerD)λ ).
déduit alors que ∀g ∈ G, on a :
Ainsi
On
∆G (fλ )(g) = tr(∆g|(ker D)λ )
= tr(g∆|(ker D)λ )
= λtr(g|(ker D)λ )
car
∆ = Id
sur
(ker D)λ
= λfλ (g)
Donc
0
0
m
∆m
G (fλ ) = λ fλ ,
et
χker D =
précédemment est continue si
Le résultat est donc vrai si
Si
le
D
s>
0
X
s
fλ = ∆m
G (h)
λ∈Sp(∆)
dim W ]
2m0
est d'ordre
. Donc
où
h
a été dénie
]
χker D ∈ H − dim W (G).
m = 2m0 .
D est d'ordre m quelconque, on a D∗ D est d'ordre 2m, et on peut appliquer
∗
∗
résultat à D D . Comme ker D = ker D D , le résultat est alors vrai pour
D.
102
Dénition 73.
On note alors
G
ind−∞,B (D)
= χker D − χker D∗
qu'on appelle indice distributionnel basique.
Remarque.
G
Si on note ind−∞,B (D)λ
G
ind−∞,B (D)
= χ(ker D)λ − χ(ker D∗ )λ ,
X
=
alors
G
ind−∞,B (D)λ .
λ∈Sp(∆)
On note Ds le prolongement de D en tant qu'opérateur borné
Ds : H s (M, E/F) → H s−m (M, E 0 /F) et on note Γ(E/F)λ , H s (M, E/F)λ le
s
noyau de l'opérateur ∆ − λId dans Γ(E/F) et H (M, E/F) respectivement.
Corollaire 14. L'opérateur D induit un opérateur Dλ : Γ(E/F)λ → Γ(E 0 /F)λ ,
et
(Ds )λ = Ds |H s (M,E/F )λ est un opérateur de Fredholm.
= χker(Ds )λ − χker(Ds∗ )λ , on a
En notant ind((Ds )λ )
G
ind−∞,B (Ds )
X
=
ind((Ds )λ ).
λ∈Sp(∆)
G
Et ind−∞,B (Ds ) est indépendant de
G
s,
ind−∞,B (Ds )
Démonstration.
L'opérateur
Remarque.
D
plus précisément
= indG
−∞,B (D).
D est G-invariant, donc D et ∆ commutent et
D induit un opérateur Dλ : Γ(E/F)λ → Γ(E 0 /F)λ .
0
Or (D, ∆ − λId) : Γ(E/F) → Γ(E/F) ⊕ Γ(E /F) a un symbole injectif.
Donc cet opérateur admet une paramétrix à gauche G-invariante notée T .
Comme T est G-invariant, T commute avec ∆ et on peut restreindre T en
0
un opérateur Tλ : Γ(E /F)λ → Γ(E/F)λ .
∗
0
De la même manière Dλ : Γ(E /F)λ → Γ(E/F)λ admet une paramétrix à
s
droite. Donc Dλ s'étend en un opérateur de Fredholm (Ds )λ : H (M, E/F) →
s−m
0
H
(M, E /F), et on sait alors que l'indice de (Ds )λ est indépendant de
s.
Si
est un opérateur diérentiel basique
(G, F)-transversalement
elliptique et si de plus
feuilletée d'un autre groupe de Lie compact
(G × H, F)-transversalement
butionnel de D sous la forme
G×H
H
D
alors
G-invariant,
commute avec l'action
D
est évidemment
elliptique. On peut alors écrire l'indice distri-
ind−∞,B (D)
=
X
α∈Ĝ,β∈Ĥ
103
cα,β χα χβ
où pour
α
xé
cα,β = 0
β.
pour presque tout
G×H
On peut donc voir ind−∞,B (D) comme une application linéaire continue de
C ∞ (G)
dans
C ∞ (H),
dénie par
φ 7→
X
Z
φχα dg.
cα,β χβ
G
α,β
6.2 Le cas des actions libres
G et H des groupes de Lie compacts. On suppose que l'action de
G × H sur M est lisse et que H agit librement sur M . On a donc un bré
principal p : M → M/H de groupe structural H au-dessus de la variété
M/H et p est une submersion G-équivariante.
Soient
Proposition 105.
G×H
F]
Soit
un feuilletage riemannien sur
Le feuilletage
M
F]
induit alors un feuilletage riemannien
G
sur
M/H
de
sur
l'action de
Démonstration.
p(L)
où
tel que l'action
F
sur
M/H
tel que
est feuilletée.
Comme l'action de
G×H
est feuilletée, la projection
p induit un feuilletage sur M/H dont les feuilles sont
L est une feuille de F ] . Le reste de la preuve est clair.
feuilletée. Donc
forme
M
est feuilletée.
Dans la suite on munit
M
p
est
de la
d'une structure riemannienne quasi-brée
(G × H)-invariante.
Proposition 106.
Soit
M/H . On note E ] le
G × H -équivariant.
Démonstration.
E
un
relevé de
F -bré vectoriel G-équivariant au-dessus de
E sur M , alors E ] est un F ] -bré vectoriel
La démonstration est similaire à la démonstration de la pro-
position 51 et est omise ici.
Notation 14. Soient E et E 0 des F -brés G-équivariants au-dessus de M/H .
Proposition 107. Soit D : Γ(E/F) → Γ(E 0 /F) un opérateur diérentiel
F -basique G-invariant
(G, F)-transversalement elliptique.
F ] -basique D] : Γ(E ] /F ] ) → Γ(E 0] /F ] )
]
qui est (G × H)-invariant et (G × H, F )-transversalement elliptique tels que
et
Alors il existe un opérateur diérentiel
le diagramme suivant est commutatif :
Γ(E ] /F ] )H
D]-
?
Γ(E/F)
D
104
Γ(E 0] /F ] )H
?
- Γ(E 0 /F)
Démonstration.
D] (σ ◦ p) = D(σ) ◦ p.
Soient (x, y) des coordonnées locales sur M/H adaptées au feuilletage F et
(x, y, t) les coordonnées locales sur M correspondantes (qui sont adaptées
]
au feuilletage F ). On remarque p(x, y, t) = p(x, y). Localement D(σ) s'écrit
X
∂α
sous la forme D(σ) =
aα (y) α1
α (σ),
∂y1 ...∂yq q
|α|≤m
X
∂α
aα (y)( α1
donc D(σ) ◦ p =
α (σ)) ◦ p,
∂y1 ...∂yq q
|α|≤m
X
∂α
]
aα (p(y, t)) α1
et D (σ ◦ p) =
α (σ ◦ p) car p(x, y, t) = p(x, y).
∂y1 ...∂yq q
Si
σ ∈ Γ(E/F),
on a
|α|≤m
Donc
D]
est un opérateur diérentiel
F ] -basique.
]
Montrons que D est
G-invariant.
Soient z ∈ M et σ ∈ Γ(E/F),
g. D] (σ ◦ p) (z) = g. D] (σ ◦ p)(g −1 .z)
= g.(D(σ)(g −1 .p(z)))
car
p
est
G-invariante
= g. (D(σ)) (p(z))
= D(g.σ)(p(z))
car
D
G-invariant
est
]
= D (g.σ ◦ p)(z).
Donc
D]
est
G-invariant.
D] est H -invariant.
Montrons que
h.(D] (σ ◦ p))(z) = h.(D(σ) ◦ p)(z)
= D(σ) ◦ p(z)
car
D(σ) ◦ p
est
H -invariante
]
= D (σ ◦ p)(z)
= D] (h.σ ◦ p)(z)
Donc
D]
est
H -invariant
et
car
σ◦p
est
H -invariante
G × H -invariant.
D] et D étant (G, F)-transversalement
(G × H, F ] )-transversalement elliptique.
En raison de la forme locale de
]
tique on déduit que D est
On note
(Wa )a∈Ĥ
un ensemble de représentants de l'ensemble des classes
de représentations irréductibles unitaires de
Wa
et
Wa = M ×H Wa
Théorème 36.
G×H
le
G-bré
H . On notera χa le caractére de
M/H associé à Wa .
vectoriel au-dessus de
Avec les notations de la proposition précédente on a
ind−∞,B (D
]
ellip-
)=
X
G
ind−∞,B (D
⊗ Wa∗ )χa ∈ C −∞ (G × H)G×H .
a∈Ĥ
105
Démonstration.
Γ(M, E ] /F ] ) est une représentation de H ,
∼
= ⊕a∈Ĥ ma Wa (Théorème de Peter-Weyl)
]
]
où ma = dim homH (Wa , Γ(M, E /F )) (Lemme de Schur).
]
]
Or homH (Wa , Γ(M, E /F )) ∼
= (Γ(M, E ] /F ] ) ⊗ Wa∗ )H .
]
∗
]
Notons que E ⊗ Wa est un F -bré et que
]
]
∗
]
∼
Γ(M, E /F ) ⊗ Wa = Γ(M, E ⊗ Wa∗ /F ] ). En eet,
]
∗
soit ∇1 une connexion basique sur le bré E . On munit le bré M × Wa
]
∗
de la connexion standard plate ∇2 et le bré E ⊗ Wa de la connexion
∇ = ∇1 ⊗ ∇ 2 .
La courbure de ∇ est donnée par R∇ = R∇1 ⊗ 1 + 1 ⊗ R∇2 .
]
De plus ∀X ∈ Γ(T F ), iX (R∇1 ) = 0 et ∇2 est plate,
]
∗
]
]
donc ∀X ∈ Γ(T F ), iX (R∇1 ⊗∇2 ) = 0, c'est-à-dire E ⊗ Wa est F -bré.
]
∗
]
∗
∼
Par ailleurs Γ(M, E ⊗ Wa ) = Γ(M, E ) ⊗ Wa . Montrons que cet isomor]
phisme induit un isomorphisme de sections basiques. Si σ ∈ Γ(M, E ) est
∗
]
∗
basique et w ∈ Wa alors σ ⊗ w est une section basique de Γ(M, E ⊗ Wa ).
En eet X ∈ Γ(T F), on a ∇1,X (σ) = 0. Donc
L'espace
]
]
donc Γ(M, E /F )
∇X (σ ⊗ w) = ∇1,X (σ) ⊗ w + σ ⊗ ∇2,X (w)
= σ ⊗ ∇2,X (w)
= σ ⊗ d(w)
=0
car
w
est un vecteur xé de
Wa∗ .
On obtient ainsi un isomorphisme
Γ(M, E ] ⊗ Wa∗ /F ] ) ∼
= Γ(M, E ] /F ] ) ⊗ Wa∗ ,
homH (Wa , Γ(M, E ] ⊗ Wa∗ /F ] )) ∼
= Γ(M, E ] ⊗ Wa∗ /F ] )H ,
]
]
∗
et homH (Wa , Γ(M, E ⊗ Wa /F )) ∼
= Γ(M/H, E ⊗ Wa∗ /F).
G×H
]
Le coecient de χa dans ind−∞,B (D ) est donc l'indice de l'opérateur
(G × H)-invariant D] ⊗ Ida : Γ(M, E ] ⊗ Wa∗ /F ] )H → Γ(M, E 0] ⊗ Wa∗ /F ] )H .
donc
Comme on a le diagramme commutatif :
Γ(M, E ] ⊗ Wa∗ /F ] )H
D] ⊗Ida
- Γ(M, E 0] ⊗ W ∗ /F ] )H
a
∼
=
∼
=
?
Γ(M/H, E ⊗
et que
H
Wa∗ )
?
- Γ(M/H, E 0 ⊗ Wa∗ )
D⊗Ida
Γ(M, E ] ⊗ Wa∗ /F ] )H ,
G×H
]
de χa dans ind−∞,B (D ) est
agit trivialement sur
on obtient que le coecient
106
G
ind−∞,B (D
⊗ Ida ).
6.3 Multiplicativité et excision
Notation 15.
Soient
(M, F) et (M 0 , F 0 ) des feuilletages riemanniens trans-
versalement orientés sur des variétés compactes connexes orientées. On munit
M0
Soient E
M
et
de métriques quasi-brées.
F -bré vectoriel au-dessus de M et E 0 un F 0 -bré vectoriel
0
0
0
au-dessus de M . On note E E le produit tensoriel externe de E et E
0
0
0
0
au-dessus de M × M , c'est-à-dire E E
(z,t) = Ez ⊗ Et , ∀(z, t) ∈ M × M .
0
0
On munit M × M du feuilletage F ⊕ F déni par :
T(z,t) (F ⊕ F 0 ) = Tz F ⊕ Tt F 0 , ∀(z, t) ∈ M × M 0 .
un
Proposition 108.
Démonstration.
E E 0 est un F ⊕ F 0 -bré vectoriel
σ ∈ Γ(E/F) et σ 0 ∈ Γ(E 0 /F), alors σ σ 0 ∈
Le bré vectoriel
0
au-dessus de M × M . De plus si
Γ(E E 0 /F ⊕ F 0 ).
Soient
∇1
et
∇2
des connexions basiques sur
E
et
E0.
E E 0 de la connexion ∇ = ∇1 ∇2 , caractérisée par
∇(σ = ∇1 (σ) σ 0 + σ ∇2 (σ 0 ), ∀σ ∈ Γ(E), ∀σ 0 ∈ Γ(E 0 ).
La courbure de ∇ est donné par R∇ = R∇1 1 + 1 R∇2 .
0
0
Soient X + X ∈ Γ(T (F ⊕ F )), on a alors :
iX+X 0 (R∇ ) = iX (R∇1 ) 1 + 1 iX 0 (R∇2 ) = 0 car ∇1 est F -basique et ∇2
0
est F -basique.
0
0
0
Donc ∇ est une connexion basique sur E E et E E est un F ⊕ F -bré.
On munit
σ0)
Le deuxième point est évident.
Proposition 109.
Sous les mêmes hypothèses, soit
m.
par A
A : Γ(E/F) → Γ(E/F)
un opérateur diérentiel basique d'ordre
On note
à = A 1
l'opérateur induit
sur
Γ(E E 0 /F ⊕ F 0 )
qui est
caractérisé par
Ã(σ σ 0 ) = A(σ) σ 0 , ∀σ ∈ Γ(E/F), ∀σ 0 ∈ Γ(E 0 /F).
Alors à est un opérateur diérentiel basique d'ordre m.
Démonstration.
Vérions d'abord que
A
induit bien un opérateur
0
0
sur Γ(E E /F ⊕ F ). On utilise encore la connexion basique ∇
1
2
1
2
On note φ, φ , φ les transports parallèles associés à ∇, ∇ , ∇ .
Par unicité du transport parallèle, on a
σ0
E 0 /F
F 0 ),
= ∇1 ∇2 .
φ = φ1 φ2 .
σ ∈ Γ(E ⊕
σ σ 0 est parallèle le long de toutes les courbes le long des feuilles
0
de F ⊕ F , c'est-à-dire si γ = (γ1 , γ2 ) est une courbe le long des feuilles de
0
0
0
t
F ⊕ F on a φt (σ σγ(0)
) = σ σγ(t)
, où φi est le transport parallèle le long
1
2 0
0
de γi (t). Ainsi φt (σγ1 (0) ) φt (σ
γ2 (0) ) = σγ1 (t) σγ2 (t) ,
1
2 0
0
et φt (σγ1 (0) ) = σγ1 (t) et φt (σ
γ2 (0) ) = σγ2 (t) .
0
C'est-à-dire σ (respectivement σ ) est parallèle le long de toutes courbes le
0
long des feuilles de F (respectivement F ).
0
0
Par conséquent σ ∈ Γ(E/F) et σ ∈ Γ(E /F).
Soit
donc
107
Ã(σ σ 0 ) = A(σ) σ 0 est bien déni et A induit un opérateur sur
Γ(E E 0 /F ⊕ F 0 ).
Soient (x, y) des coordonnées locales sur M adaptées au feuilletage F et (k, l)
0
0
des coordonnées locales sur M adaptées au feuilletage F . Donc (x, y, k, l)
0
0
sont des coordonnées locales sur M × M adaptées au feuilletage F ⊕ F .
α
P
∂
Localement A s'écrit sous la forme A =
α
|α|≤m aα (y)
α1
∂y1 ...∂yq q
où aα (y) ∈ hom(E(x,y) , E(x,y) ).
P
∂α
Ainsi à =
a
(y)
1
α
|α|≤m α
∂y1α1 ...∂yq q
0
0
où aα (y) 1 ∈ hom(E E
(x,y,k,l) , E E(x,y,k,l) ).
Donc
On en conclut que
Ã
est basique.
Corollaire 15.
Sous les mêmes hypotheses,
Démonstration.
Le calcul du symbole est évident au vu de la démonstration
∀(z, t) ∈ M × N, ∀ξ ∈ ν ∗ F, σ(Ã)((z, t), ξ) = σ(A)(z, ξ) 1.
De plus si A est F -transversalement elliptique alors à est
F ⊕ F 0 -transversalement elliptique.
précédente.
On utilisera les identications suivantes :
∼
×
= Tz∗ M ⊕ Tt∗ M 0 .
0
brés T F et T F s'identient
∗ (M
T(z,t)
Les
M 0)
T(z,t) (M × M 0 ) ∼
= Tz M ⊕ Tt M 0
à des parties de
T ∗ (M × M 0 ).
et
De plus on
a :
ν ∗ (F ⊕ F 0 ) ∼
= {ξ ∈ T ∗ (M × M 0 )/ξ(X) = 0, ∀X ∈ Γ(T (F ⊕ F 0 ))}
∼
= {ξ ∈ T ∗ (M × M 0 )/ξ(X) = 0, ∀X ∈ Γ(T F ⊕ T F 0 )}
∼
= {ξ ∈ T ∗ (M × M 0 )/ξ(X) = 0, ∀X ∈ Γ(T F)}
∩ {ξ ∈ T ∗ (M × M 0 )/ξ(X) = 0, ∀X ∈ Γ(T F 0 )}
∼
= {ξ1 + ξ2 ∈ T ∗ M ⊕ T ∗ M 0 /ξ1 (X) + ξ2 (X) = 0, ∀X ∈ Γ(T F)}
∩ {ξ1 + ξ2 ∈ T ∗ M ⊕ T ∗ M 0 /ξ1 (X) + ξ2 (X) = 0, ∀X ∈ Γ(T F 0 )}.
ξ2 ∈ T ∗ M 0 , on a ξ2 (X) = 0, ∀X ∈ Γ(T M ) et si ξ1 ∈ T ∗ M , on a
ξ1 (X) = 0, ∀X ∈ Γ(T M 0 ). Donc ν ∗ (F ⊕ F 0 ) est isomorphe à
{ξ ∈ T ∗ M/ξ(X) = 0, ∀X ∈ Γ(T F)}∩{ξ ∈ T ∗ M 0 /ξ(X) = 0, ∀X ∈ Γ(T F 0 )},
∗
0
∗
∗ 0
et ν (F ⊕ F ) est isomorphe à ν F ∩ ν F .
∗
Or σ(A)(z, ξ) est inversible si ξ ∈ ν F , donc σ(Ã)((z, t), ξ) est inversible
∗
0
0
si ξ ∈ ν (F ⊕ F ), et à est F ⊕ F -transversalement elliptique.
Or si
Proposition 110.
E → M un F -bré vectoriel et E 0 → M 0 un
A : Γ(E/F) → Γ(E/F) un opérateur diérentiel basique
F -transversalement elliptique d'ordre m et B : Γ(E 0 /F) → Γ(E 0 /F) un opé0
rateur diérentiel basique d'ordre m F -transversalement elliptique.
Soient
F 0 -bré vectoriel,
108
à et B̃
commutent.
à −B̃ ∗
(ii) On note A]B =
. Alors A]B est un opérateur diérentiel
B̃ Ã∗
σ(A) 1 −1 σ(B)∗
basique d'ordre m et σ(A]B) =
.
1 σ(B) σ(A)∗ 1
0
De plus A]B est F ⊕ F -transversalement elliptique.
(i) Alors les opérateurs
Démonstration.
Ã(σ (i) Soient
σ0)
= A(σ) σ ∈ Γ(E/F)
et
σ 0 ∈ Γ(E 0 /F),
on a
σ0.
B̃(Ã(σ σ 0 )) = B̃(A(σ) σ 0 )
= A(σ) B(σ 0 )
= Ã(σ B(σ 0 ))
= Ã(B̃(σ σ 0 )).
Donc
Ã
et
B̃
commutent.
(ii) Le deuxième point découle des propositions précédentes.
Notation 16.
Soient
G, H
des groupes de Lie compacts. Dans la suite on
suppose qu'on a une action lisse de
sur
G
sur
M
et une action lisse de
G×H
M 0.
On suppose de plus que ces actions sont feuilletées, que
structure riemannienne quasi-brée
G-invariante
et
M0
(G × H)-invariante.
que E est un bré G-équivariant
M
est munie d'une
d'une structure rie-
mannienne quasi-brée
On suppose de plus
et que
E0
est un bré
(G × H)-équivariant.
G × H sur M × M 0 donnée par
(g, h).(z, t) = (g.z, (g, h).t), ∀(g, h) ∈ G × H, ∀(z, t) ∈ M × M 0 et E E 0
est un bré (G × H)-équivariant.
On a une action lisse feuilletée de
Théorème 37.
Soient A : Γ(E/F) → Γ(E/F) un opérateur diérentiel baG-invariant (G, F)-transversalement elliptique et
B : Γ(E 0 /F) → Γ(E 0 /F) un opérateur diérentiel basique (G × H)-invariant
0
et (G × H, F )-transversalement elliptique. Alors A]B est un opérateur dif0
férentiel basique (G × H, F ⊕ F )-transversalement elliptique et
sique
G×H
ind−∞,B (A]B)
= indG
−∞,B (A)
G×H
ind−∞,B (B)
∈ C −∞ (G × H).
Nous allons utiliser plusieurs lemmes.
Lemme 13.
L'opérateur
A]B
est
(G × H)-invariant
transversalement elliptique.
109
et
(G × H, F ⊕ F 0 )-
Démonstration.
Soient
Montrons que A]B est (G × H)-invariant.
σ ∈ Γ(E/F), σ 0 ∈ Γ(E 0 /F), et (g, h) ∈ G × H ,
Ã((g, h).(σ σ 0 )) = Ã g.σ (g, h).σ 0
= A(g.σ) (g, h).σ 0
= g.A(σ) (g, h).σ 0
car
A
est
G-invariant
0
= (g, h).(A(σ) σ )
= (g, h).(Ã(σ σ 0 )).
à est (G × H)-invariant. De même B̃ est (G × H)-invariant.
A]B est (G × H)-invariant.
0
Montrons que A]B est un opérateur (G × H, F ⊕ F )-transversalement ellip0
tique. Soit (z, t) ∈ M × M , on a :
(T(z,t) ΘG×H (z, t) + T(z,t) (F ⊕ F 0 ))⊥ = (T(z,t) ΘG×H (z, t) + Tz F + Tt F 0 )∗ .
∗ 0
0
∗
∗
G×H (z, t)+T
0 ⊥ ∼
Donc (T(z,t) Θ
(z,t) (F ⊕F )) = (TG×H (M ×M ))(z,t) ∩νz F ∩νt F .
Or l'orbite de z dans M sous l'action de G est contenue dans l'orbite de (z, t)
0
dans M × M sous l'action de G × H ,
G
G×H (z, t) et (T ∗
0
∗
ainsi Tz Θ (z) ⊂ T(z,t) Θ
G×H (M × M ))(z,t) ⊂ (TG M )z .
Or A est (G, F)-transversalement elliptique,
∗
∗
donc ∀ξ ∈ (TG M )z ∩ νz F, σ(Ã)((z, t), ξ) est inversible.
0
∗
∗
En particulier ∀ξ ∈ (TG×H (M ×M ))(z,t) ∩νz F, σ(Ã)((z, t), ξ) est inversible.
0
Or B est (G × H, F )-transversalement elliptique,
∗
0
∗ 0
donc ∀ξ ∈ (TG×H (M × M ))(z,t) ∩ νt F , σ(B̃)((z, t), ξ) est inversible.
G×H (z, t) +
On en déduit que σ(A]B)((z, t), ξ) est inversible ∀ξ ∈ (T(z,t) Θ
0
∗
T(z,t) (F ⊕ F )) ,
0
c'est-à-dire que A]B est (G × H, F ⊕ F )-transversalement elliptique.
Donc
Ainsi
Lemme 14.
Les noyaux de
A]B
et de
(A]B)∗
sont donnés par :
ker(A]B) = ⊕λ ker A (ker B)λ ⊕ ⊕λ ker A∗ (ker B ∗ )λ ,
ker((A]B)∗ ) = ⊕λ ker A∗ (ker B)λ ⊕ ⊕λ ker A (ker B ∗ )λ .
Démonstration. On
∗note P0∗, Q0 , P1 , Q1
les opérateurs dénis par :
à à + B̃ B̃
0
P0 0
=
=
et
0 Q0
0
ÃÃ∗ + B̃ B̃ ∗
ÃÃ∗ + B̃ ∗ B̃
0
P1 0
∗
(A]B)(A]B) =
=
0 Q1
0
Ã∗ Ã + B̃ B̃ ∗
Les opérateurs P0 , Q0 , P1 , Q1 sont des opérateurs diérentiels basiques G×H
(A]B)∗ (A]B)
invariants.
ker(A]B) = ker((A]B)∗ (A]B)) = ker P0 ⊕ ker Q0 ,
ker((A]B)∗ ) = ker((A]B)(A]B)∗ ) = ker P1 ⊕ ker Q1 .
On a ker à ∩ ker B̃ ⊂ ker P0 .
On a
110
et
σ ∈ Γ(E E 0 /F ⊕ F 0 ) ⊕ Γ(E E 0 /F ⊕ F 0 ),
hP0 (σ), σi = hÃ(σ), Ã(σ)i + hB̃(σ), B̃(σ)i, donc ker P0 = ker à ∩ ker B̃ .
Or ker B̃ est formé de sections basiques σ(z, t) telles que
∀z ∈ M, σ(z, .) ∈ ker B .
On écrit ker B = ⊕λ (ker B)λ la décomposition de ker B en fonction des
valeurs propres de ∆H comme dans la démonstration du théorème 35.
De même on écrit ker B̃ = ⊕λ (ker B̃)λ et ker P0 = ⊕λ (ker P0 )λ .
Donc (ker B̃)λ est l'espace des sections lisses basiques du bré vectoriel plat
KBλ = M × (ker B)λ au-dessus de M .
Or à commute avec B̃ et ∆H , donc à induit un opérateur sur (ker B̃)λ ,
c'est-à-dire sur les sections basiques de KBλ .
Or à = A 1, donc l'opérateur induit est A 1KB .
λ
Or ker P0 est formé par les sections basiques de ker B̃ annulées par Ã,
ainsi (ker P0 )λ est formé par les sections basiques de (ker B̃)λ annulées par
Ã, donc (ker P0 )λ = ker(A 1KBλ ) = ker A (ker B)λ .
∗
∗
En permutant Ã, Ã , B̃ et B̃ on obtient :
Soit
ker(A]B) = ker P0 ⊕ ker Q0
= ⊕λ ker A (ker B)λ ⊕ ⊕λ ker A∗ (ker B ∗ )λ
ker((A]B)∗ ) = ker P1 ⊕ ker Q1
= ⊕λ ker A∗ (ker B)λ ⊕ ⊕λ ker A (ker B ∗ )λ
Revenons à la démonstration du théorème 37.
Démonstration
En appliquant les lemmes précédents on a,
X du théorème 37. X
χker(A]B) =
χker A(ker B)λ +
λ
χker A∗ (ker B ∗ )λ .
λ
ker A (ker B)λ est une représentation de G × H de la forme
π(g, h) = π1 (g) ⊗ π2 (g, h), ainsi χker A(ker B)λ = χker A χ(ker B)λ .
X
X
Par conséquent χker(A]B) =
χker A χ(ker B)λ +
χker A∗ χ(ker B ∗ )λ ,
Or
λ
G×H
ind−∞,B (A]B)
=
X
χker A χ(ker B)λ +
X
λ
−
X
=
X
=
X
λ
λ
et
λ
χker A∗ χ(ker B ∗ )λ
λ
χker A∗ χ(ker B)λ +
X
χker A χ(ker B ∗ )λ
λ
G×H
χker A ind−∞,B (B)λ −
X
λ
G×H
G
ind−∞,B (A)ind−∞,B (B)λ
λ
G×H
= indG
−∞,B (A)ind−∞,B (B).
111
χker A indG×H
−∞,B (B)λ
Remarque. Comme B est un opérateur diérentiel basique (G×H)-invariant
(G × H, F 0 )-transversalement elliptique
X on peut écrire son indice distribuG×H
tionnel sous la forme ind−∞,B (B) =
cα,β χα χβ .
et
α,β
(ker B ∗ )λ sont de dimension nies on a un nombre ni
d'indices alpha tel que cα,β 6= 0.
G
−∞ (G) et indG×H (B) ∈ C −∞ (G × H)
Donc le produit de ind−∞,B (A) ∈ C
−∞,B
Comme
(ker B)λ
et
est bien déni.
φ ∈ C ∞ (H) et ψ ∈ C ∞ (G) on a :
G×H
G×H
G
ind−∞,B (A]B)(ψ ⊗ φ) = ind−∞,B (ψ ind−∞,B (B)(φ)).
Si
Nous allons maintenant étudier la propriété d'excision pour l'indice distributionnel basique.
Notation 17. Soit U une variété non-compacte munie d'un feuilletage riemmanien
F 0 et
G.
j : U → M tel que j est feuilletée et
plus que j(U ) est saturé dans M .
d'une action lisse feuilletée du groupe de Lie compact
On suppose qu'on a un plongement
G-équivariante,
et on suppose de
F 0 -bré G-équivariant tel que E est trivial en dehors
de la saturation d'un compact de U . L'application j est un diéomorphisme
local de U sur j(U ), donc on peut dénir le bré vectoriel poussé-en-avant
j∗ (E).
Soit
E → U
un
Proposition 111.
dessus de
j(U )
Le bré vectoriel
et se prolonge en un
j∗ (E) est un F -bré G-équivariant auF -bré G-équivariant au-dessus de M .
Démonstration.
Comme E est G-équivariant et j est G-équivariante, j∗ (E)
G-équivariant au-dessus de j(U ).
0
Soient (x, y) des coordonnées locales sur U adaptées au feuilletage F ,
comme j est un diéomorphisme local qui préserve le feuilletage,
(x◦j −1 , y ◦j −1 ) sont des coordonnées locales sur j(U ) adaptées au feuilletage
F . E étant un F 0 -bré au-dessus de U , on munit j∗ (E) de la connexion
induite par une connexion basique sur E .
Donc j∗ (E) est un F -bré, et j∗ (E) est trivial en dehors de la saturation
d'un compact de j(U ). Puisque j(U ) est un ouvert saturé, on prolonge j∗ (E)
par un bré au-dessus de M qui est trivial en-dehors de j(U ) et qu'on note
j! (E). Montrons maintenant que j! (E) est un F -bré. Si j(U ) est dense alors
le résultat est immédiat et on peut donc réduire au cas où j(U ) n'est pas
dense dans M . En utilisant les résultats de [Hae88], voir aussi [EKAN93],
il est facile de montrer qu'il existe un voisinage tubulaire ouvert N saturé
(même pour les fermetures de feuilles) du bord de U dans M ainsi qu'une
fonction ϕ̃ sur M tels que
ϕ̃ est une fonction basique pour les fermetures de feuilles de F , et donc
∞ sur M ;
pour F , qui est de plus de classe C
est
112
0 ≤ ϕ̃ ≤ 1 ;
La restriction de
La restriction de
ϕ̃
ϕ̃
à
U
au complémentaire de
En utilisant la fonction basique
sur
j! (E)
1;
N dans U c
est identiquement égale à
ϕ̃,
est égale à
0.
on construit alors une connexion basique
.
Proposition 112. Sous les mêmes hypothèses, soit D : Γ(E/F 0 ) → Γ(E 0 /F 0 )
G-invariant (G, F 0 )-transversalement elliptique tel qu'en dehors de la saturation d'un compact de U , D = Id modulo
0
les trivialisations de E et E . Alors D induit un opérateur diérentiel basique
G-invariant (G, F)-transversalement elliptique sur j(U ), qu'on note j∗ (D),
et qui se prolonge en dehors de j(U ) par l'identité.
un opérateur diérentiel basique
Démonstration.
On a
j∗ (D) = j∗ ◦ D ◦ j∗−1 .
Montrons que
j∗ (D)
est
G-
invariant.
Soient
σ ◦ j ∈ Γ(j∗ (E)/F), z ∈ j(U ),
et
g ∈ G,
j∗ (D) (g.((σ ◦ j)z )) = j∗ (D)(g.(σg−1 .j(z) ))
= j∗ ◦ D(g.(σj −1 (g−1 .j(z)) ))
= j∗ ◦ D(g.(σg−1 .z ))
car
j −1
est
G-équivariante
= j∗ ◦ D((g.σ)z )
= j∗ (g.(D(σ)z )
= g.(j∗ ◦ D(σ)z )
car
car
D
est
G-invariant
j
est
G-équivariante
= g.(j∗ ◦ D ◦ j∗−1 (σj(z) ))
= g.(j∗ (D)((σ ◦ j)z )).
Donc
j∗ (D)
est
G-invariant.
(x, y) sur U et (x ◦ j −1 , y ◦ j −1 ) sur j(U )
de la proposition précédente on constate que j∗ (D) est F -basique,
−1 (z), ξ), donc j (D) est (G, F)-transversalement
et que σ(j∗ (D))(z, ξ) = σ(D)(j
∗
En utilisant les coordonnées locales
elliptique.
Théorème 38.
G
Sous les mêmes hypothèses, ind−∞,B (j∗ (D)) est indépendant du choix de j .
Démonstration.
en dehors de
σ ∈ Γ(j∗ (E)/F),
j(U ), j∗ (D) est égal à l'identité,
donc
D(σ ◦ j) = 0 ⇔ supp(σ ◦ j) ⊂ U
et
D(σ) = 0
⇔ supp(σ) ⊂ j(U )
et
j∗ (D)(σ) = 0.
Soit
ker j∗ (D) = ker D. De même ker j∗ (D)∗ = ker D∗ . Comme j∗ (D) est
opérateur (G, F)-transversallement elliptique sur une variété fermée, il
Donc
un
113
admet un indice distributionnel basique. Par conséquent
D
admet un indice
distributionnel basique et comme ces deux opérateurs ont les mêmes noyaux
G
on a ind−∞,B (j∗ (D))
= indG
−∞,B (D).
6.4 Lien avec l'indice basique et l'indice équivariant
Nous reprenons les notations de la section 4.1.
Nous allons maintenant étudier le problème de l'indice basique dans le cas où
la variété
F
M
est munie d'un feuilletage riemannien transversalement orienté
G.
H = SO(q) et on suppose que dim W ] > 0.
0
0
Soient E et E des F -brés G-équivariant et D : Γ(E/F) → Γ(E /F) un
opérateur diérentiel basique G-invariant (G, F)-transversalement elliptique
0
d'ordre m = 2m .
On a vu précédemment que D admet un indice distributionnel basique
G
ind−∞,B (D).
et d'une action feuilletée d'un groupe de Lie compact
On note
Lemme 15.
de
G
sur
G sur M se relève en une action feuilletée
G sur M ] commute avec l'action de H et
G × H sur M ] .
L'action feuilletée de
M ].
De plus l'action de
on a une action feuilletée de
Démonstration.
Evident.
Lemme 16. Le F -bré G-équivariant E au-dessus de M
F ] -bré G × H -équivariant au-dessus de M ] noté E ] .
Démonstration.
se relève en un
La démonstration est similaire à la démonstration de la pro-
position 51.
Lemme 17.
(i) L'action feuilletée de
G×H
sur
(M ] , F ] )
induit une
]
sur W .
G×H
]
(ii) Comme Ēu = Γ(Lu , E/F), ∀u ∈ W , l'action de G × H sur E induit
une action sur le bré utile Ē .
(iii) De plus on a trivialement que l'application ψ : Γ(E/F) → Γ(Ē) est
(G × H)-invariante.
action de
Démonstration.
Evident.
Proposition 113.
M ] en un opérateur
:
→
(G × H)-invariant
]
(G × H, F )-transversalement elliptique d'ordre m.
G×H
]
]
En particulier D admet un indice distributionnel basique ind−∞,B (D ).
D]
Γ(E ] /F ] )
Démonstration.
L'opérateur
D
se relève sur
Γ(E 0] /F ] ) qui est basique
Evident.
114
Théorème 39.
On rappelle que l'opérateur
D]
induit un opérateur
D̄ : Γ(Ē) →
Γ(Ē 0 ) , et que ces deux opérateurs sont conjugués.
L'opérateur
D̄
est donc
(G × H)-invariant (G × H)-transversalement
ellip-
G×H
tique et admet par conséquent un indice distributionnel ind−∞ (D̄) au sens
d'Atiyah (voir [Ati]). De plus ces deux opérateurs ont le même indice distributionnel, c'est-à-dire
G×H
ind−∞,B (D
Démonstration.
Les opérateurs
D̄
]
) = indG×H
−∞ (D̄).
et
D]
sont conjugués,
donc ils ont les mêmes noyaux et conoyaux. D'où le résultat.
Théorème 40.
Alors l'indice
]
H = D̄
D],H = D|Γ(E
] /F ] )H et D̄
|Γ(Ē)H .
distributionnel basique de D est donné par
On note
G
ind−∞,B (D)
Démonstration.
],H
H
= indG
) = indG
−∞,B (D
−∞ (D̄ ).
Le résultat est une conséquence immédiate des isomorphismes
Γ(E/F) ∼
= Γ(E ] /F ] )H ∼
= Γ(Ē)H
]
proviennent de la dénition de D .
suivants
et
ker D ∼
= ker D],H ∼
= ker D̄H , qui
Remarque. Pour G = {e} on retrouve le problème posé par El-Kacimi dans
[EKA90].
Remarque.
G×H
On a ind−∞
(D̄) =
X
−
(m+
ρ − mρ )χρ
ˆ
ρ∈G×H
G×H
∗
−
)χρ .
− mρ = ind((D̄ ⊗ Wρ )
X
G
H
+
−
Et ind−∞ (D̄ ) =
(ma − ma )χa où m+
a
où
m+
ρ
H
∗ G
− m−
a = ind((D̄ ⊗ Va ) )χa .
a∈Ĝ
Théorème 41.
On a ind((D̄
H
⊗ Va∗ )G ) = ind((D ⊗ Va∗ )G×H ), ∀a ∈ Ĝ.
Autrement dit
G×H
H
hindG
−∞ (D̄ ), χa i = hind−∞ (D̄), χa ⊗ 1H i
et
G×H
hindG
−∞,B (D), χa i = hind−∞ (D̄), χa ⊗ 1H i.
Démonstration.
Si
(π, Va )
On notera
D̄H ⊗ Va∗ = D̄H ⊗ 1a
où 1a = IdV ∗ .
a
G, alors (π, Va ) induit une
par (π̃, Va ) où π̃(g, h) = π(g)
est une représentation irréductible de
G × H donnée
(π̃, Va ) = (π ⊗ 1H , Va ).
∗
∗
que D̄ ⊗ 1a : Γ(Ē) ⊗ Va → Γ(Ē 0 ) ⊗ Va
représentation irréductible de
c'est-à-dire
Montrons
115
est
(G × H)-invariant.
Soient
(g, h) ∈ G × H, σ ∈ Γ(Ē)
et
v ∈ Va∗ ,
on a
D̄ ⊗ 1a ((g, h).(σ ⊗ v)) = D̄ ⊗ 1a ((g, h).σ, g.v)
= D̄((g, h).σ) ⊗ g.v
= (g, h).D̄(σ) ⊗ g.v
car
D̄
est
(G × H)-invariant
= (g, h).(D̄(σ ⊗ v))
= (g, h).(D̄ ⊗ 1a (σ ⊗ v)).
Γ(Ē) ⊗ Va∗ est engendré par des éléments de la forme σ ⊗ v on a que
D̄ ⊗ 1a est (G × H)-invariant.
H G
G×H où P G×H = P
On note P = D̄⊗1a . Montrons que (P ) = P
|(Γ(Ē)⊗Va∗ )G×H
H
H
G
H
et P
= P|(Γ(Ē)⊗Va∗ )H et (P ) = P|((Γ(Ē)⊗V ∗ )H )G .
Comme
a
(Γ(Ē) ⊗ Va∗ )G×H = {s ∈ Γ(Ē) ⊗ Va∗ /∀(g, h) ∈ G × H, (g, h).s = s},
(Γ(Ē) ⊗ Va∗ )H = {s ∈ Γ(Ē) ⊗ Va∗ /∀h ∈ H, h.s = s}, et
On a
et
((Γ(Ē) ⊗ Va∗ )H )G = {s ∈ (Γ(Ē) ⊗ Va∗ )H /∀g ∈ G, g.s = s}
= {s ∈ Γ(Ē) ⊗ Va∗ /∀h ∈ H, h.s = s
=
=
{s ∈ Γ(Ē) ⊗ Va∗ /∀(g, h)
(Γ(Ē) ⊗ Va∗ )G×H
(P H )G = P G×H . Montrons
∗
Soient σ ∈ Γ(Ē) et v ∈ Va . On a
Donc
que
et
∀g ∈ G, g.s = s}
∈ G × H, (g, h).s = s}
(Γ(Ē) ⊗ Va∗ )H = Γ(Ē)H ⊗ Va∗ .
σ ⊗ v ∈ (Γ(Ē) ⊗ Va∗ )H ⇔ ∀h ∈ H, h.(σ ⊗ v) = σ ⊗ v
⇔ ∀h ∈ H, h.σ ⊗ v = σ ⊗ v
⇔ σ ∈ Γ(Ē)H .
Γ(Ē) ⊗ Va∗ est engendré par des éléments de la forme σ ⊗ v on déduit
∗ H = Γ(Ē)H ⊗ V ∗ .
que (Γ(Ē) ⊗ Va )
a
H
∗ G
∗ H G
∗ G×H .
Montrons que ind((D̄ ⊗ Va ) ) = ind(((D̄ ⊗ Va ) ) ) = ind((D ⊗ Va )
H
∗
∗ H
Or Γ(Ē) ⊗ Va = (Γ(Ē) ⊗ Va ) ,
H
∗
G
donc (Γ(Ē)
⊗ Va ) = ((Γ(Ē) ⊗ Va∗ )H )G = (Γ(Ē) ⊗ Va∗ )G×H . D'où le
Comme
résultat.
Problème ouvert.
Calculer l'indice distributionnel basique en fonctions
d'invariants transverses au feuilletage.
116
Annexe A
Généralités sur les feuilletages
et théorie de Molino
Nous allons rappeler les premières notions sur les feuilletages. Nous rappellerons également la construction des feuilletages par suspension, la notion
de structure transverse, en particulier la dénition des feuilletages riemanniens qui est l'objet de ce manuscrit, et enn la notion d'holonomie(voir par
exemple [Mol88, MM03, Ton97, EKAB84]).
A.1 Premières dénitions
Soit
(M, g)
une variété riemannienne compacte connexe orientée sans
n.
bord de dimension
Dénition 74.
atlas maximal
F de codimension q sur M est la donnée d'un
ϕi : Rn → Ui est un diéomorphisme qui véri-
Un feuilletage
(Ui , ϕi )i∈I
où
e :
si
Ui ∩ Uj
est non-vide, le changement de cartes
est de la forme
x0 = ϕij (x, y)
et
y 0 = γij (y).
0 0
ϕ−1
j ◦ ϕi : (x, y) 7→ (x , y )
Un tel atlas est dit feuilleté et de telles cartes sont appelées des cartes feuilletées.
π : Rn = Rp × Rq → Rq la seconde projection. On appelle plaque du
−1
feuilletage F les bres de l'application π ◦ ϕi .
La variété M est décomposée en sous-variétés connexes de dimension p. Ces
sous-variétés sont appelées les feuilles de F et sont une réunion de plaques.
Soit
Proposition 114.
un atlas maximal
Soit F un feuilletage de codimension q sur M donné par
q
(Ui , ϕi )i∈I . Alors l'application fi = π ◦ ϕ−1
i : Ui → R est
une submersion.
De plus si
Ui ∩ Uj
est non-vide, on a
fj = γij ◦ fi
relation de cocycle.
117
et les
(γij )ij
vérient une
Les submersions
fi
et les diéomorphismes
tement le feuilletage
Remarque.
γij
de
Rq
caractérisent complè-
F.
On peut alors donner une dénition alternative de la notion de
feuilletage.
Dénition 75.
On appelle feuilletage sur M la donnée d'un recouvrement
(Ui )i∈I de M , et d'une famille de submersions fi : Ui → T sur une
variété T de dimension q (appelée variété transverse) qui vérie :
∀i, j tels que Ui ∩ Uj est non-vide on a fj = γji ◦ fi où
γji : fi (Ui ∩ Uj ) → fj (Ui ∩ Uj ) sont des diéomorphismes qui vérient une
ouvert
condition de cocycle.
On dit que
(Ui , fi , T, γij )
est un cocycle feuilleté dénissant
F.
Dénition 76.
Soit F un feuilletage sur M , si x ∈ M on note Tx F l'espace
x à la feuille contenant x.
T F = qx∈M Tx F , T F est appellé l'espace tangent au feuilletage.
tangent en
On note
Remarque.
TF
L'espace tangent au feuilletage
involutif de dimension
p
de
est un sous-bré vectoriel
TM.
De plus par le théorème de Frobenius, le feuilletage
ractérisé par la donnée de
Exemple 18.
F
est entièrement ca-
T F.
p : M → B est une submersion, alors les composantes
connexes des bres de p dénissent un feuilletage sur M .
En particulier si M est de la forme M = F × B , on peut munir M du
feuilletage dont les feuilles sont les ensembles de la forme F × {b}, b ∈ B .
Si
Exemple 19.
Soit π : M → B une bration avec dim M = n et dim B = q .
π est une submersion et que T M = V (M ) ⊕ H(M ) où
V (M ) = Ker π∗ et π∗ induit un isomorphisme de H(M ) sur T B .
Alors V (M ) est un sous-bré involutif de T M et dénit un feuilletage sur
M de codimension q dont les feuilles sont les bres de la bration.
On sait que
Dénition 77.
Si
Dénition 78.
On dit que le feuilletage
M et (M 0 , F 0 ) est une autre
f : M → M 0 est feuilletée si
0
pour toute feuille L de F , f (L) est contenue dans une feuille de F , ou de
0
manière équivalente si f∗ (T F) ⊂ T F .
F
est un feuilletage sur
∞
variété feuilletée, on dira que l'application C
F
est simple, si
F
est déni par
une submersion dont les bres sont connexes.
Dénition 79.
restreint à
U
Remarque.
On dit qu'un ouvert
U
de
M
est simple, si le feuilletage
F
est un feuilletage simple.
Tout point de
M
possède un voisinage ouvert qui est un ouvert
simple.
118
Dénition 80. Soit U une partie de M , on dit que U est saturé pour F , si
U est une réunion de feuilles, autrement dit si la feuille passant par un point
x de U est contenue dans U .
Dénition 81.
Soit
T
une sous-variété de
est une transversale si en tout point de
T
M
de dimension
l'espace tangent
q , on dit que T
à T est supplé-
mentaire à l'espace tangent au feuilletage en ce point.
On dit qu'une transversale est totale si elle rencontre toute les feuilles du
feuilletage
Remarque.
(i) Un feuilletage admet toujours au moins une transversale
totale.
(ii) En tout point de
Remarque.
M
il passe au moins toujours une transversale.
Nous allons à présent rappeler la construction des feuilletages
par suspension qui nous sera utile pour fournir des exemples de feuilletages.
Dénition 82.
B et T des variétés connexes de dimension p et q
h : π1 (B) → Dif f (T ) un morphisme de groupes où π1 (B)
désigne le groupe fondamental de B .
On note M̃ = B̃ × T où B̃ désigne le revêtement universel de B et p̃ : B̃ → B
Soient
respectivement, et
la projection associée.
Proposition 115.
On a une action
C∞
de
π1 (B)
sur
M̃
dénie par
L[γ] (x̃, y) = ([γ].x̃, h([γ])(y)), ∀x̃ ∈ B̃, ∀y ∈ T.
On notera
M = M̃ /π1 (B)
la variété quotient et
π : M̃ → M
la surjection
canonique.
Proposition 116.
On munit
M̃
d'un feuilletage de codimension
q
noté
F̃
T B̃ dont les feuilles sont de la forme B̃ × {y}, y ∈ T .
L[γ] envoie une feuille de F̃ sur une feuille de F̃ , on peut dénir un
feuilletage F sur M de codimension q dont les feuilles sont de la forme π(L̃)
ou L̃ est une feuille de F̃ .
Le feuilletage (M, F) est alors appelé feuilletage par suspension du morphisme h.
déni par
Comme
Remarque.
p̃ induit une bation localement triviale
T . On voit alors que les bres de p sont des transversales
totales et connexes du feuilletage (M, F) (on dit que le feuilletage F est
transverse à la bration p).
La variété T s'identie alors à une transversale de (M, F).
p:M →B
L'application
de bre
Exemple 20.
On considère le feuilletage où
B
est le cercle
S1
et
T = S1.
B̃ = R et π1 (B) = Z. On dénit le morphisme de groupe
ρ : π1 (B) → Dif f (T ) par ρ(1) = Me2πiθ où Me2πiθ désigne la multiplication
Donc
119
par
e2πiθ .
On obtient alors un feuilletage sur le tore
T 2.
θ est rationnel les feuilles sont diéomorphes au cercle S 1 , sinon les feuilles
sont isomorphes à la droite réelle R (et elles sont denses).
Si
A.2 Structures transverses
(Ui , fi , T, γij )
M.
Soit
variété
un cocycle feuilleté dénissant le feuilletage
Une structure transverse à
Remarque.
F
est une structure sur
T
F
sur la
invariante par les
On appelle espace des feuilles l'espace quotient
M/F
γij .
(c'est-à-
dire deux points sont équivalents s'ils appartiennent à la même feuille) muni
de la topologie quotient.
En fonction du feuilletage
F
la topologie de
M/F
peut-être radicalement
diérente (voir par exemple [Mol88]).
M/F dière d'une
F comme une structure
que M/F ne soit pas muni
Plus le feuilletage dière d'un feuilletage simple, plus
variété. On peut voir une structure transverse sur
M/F ,
géométrique sur l'epace des feuilles
bien
d'une structure de variété en général.
Dénition 83.
T est une variété riemannienne et
F est un feuilletage riemmannien.
Si
tries, on dira que
les
γij
sont des isomé-
Proposition 117. Le feuilletage F est riemannien si et seulement si on peut
M d'une métrique riemmanienne g tel que :
(i) ker gx = Tx F, ∀x ∈ M ,
(ii) LV (g) = 0, ∀V ∈ Γ(T F) où
LV (g)(X, Y ) = V (g(X, Y )) − g(LV (X), Y ) − g(X, LV (Y )).
munir
Dénition 84.
on dira que
F
Remarque.
Si la variété
T
admet un parallélisme invariant par les
γij ,
est transversalement parallélisable.
Si
F
est un feuilletage transversalement parallélisable, alors
F
est un feuilletage riemannien. En eet : il sut de dénir la métrique riemannienne sur le bré normal
sur toute la variété
Dénition 85.
dira que
F
Si
M
T
νF = T M/T F
en un point et de la transporter
à l'aide du parallélisme transverse.
est un groupe de Lie et les
γij
sont des translations, on
est un feuilletage de Lie.
Remarque.
Un feuilletage de Lie est transversalement parallélisable. En
eet : tout groupe de Lie est parallélisable et on peut toujours choisir un
parallélisme invariant par translation à gauche.
Dénition 86.
que
F
Si
T
est orientable et les
est transversalement orientable.
120
γij
préservent l'orientation on dira
Proposition 118.
Dénition 87.
Si
T
Si
spin, on dira que
Exemple 21.
F
T
orientable si et
est une variété analytique complexe et les
biholomorphes, on dira que
Dénition 88.
F est transversalement
νF = T M/T F est orientable.
Le feuilletage
seulement si le bré normal
F
γij
sont
est transversalement holomorphe.
est une variété spin et les
γij
préservent la structure
est transversalement spin.
π : M → B,
Dans le cas d'un feuilletage par bration
structure transverse au feuilletage
structure géométrique sur la base
F
B.
une
est exactement le tiré-en-arrière d'une
Exemple 22. Dans le cas d'un feuilletage par suspension M = B̃ ×T /π1 (B)
du morphisme
h,
une structure transverse au feuilletage
une structure géométrique sur
T
F
est exactement
invariante par l'action du groupe
Γ = h(π1 (B)).
A.3 Holonomie
Dans ce paragraphe nous allons rappeler la notion d'holonomie (voir par
exemple [CC00, Mol88, MM03, EKAB84, Ton97]).
L une feuille de F , x0 , x00
0
en x et x .
Soient
passant
Proposition 119.
une submersion
des points de
On suppose que
π:M →W
F
L et T, T 0
des transversales
est un feuilletage simple déni par
dont les bres sont connexes.
x00 sont dans la même feuille, on a π(x0 ) = π(x00 ).
L'application π induit des diéomorphismes locaux d'un ouvert V de T sur
W et d'un ouvert V 0 de T 0 sur W .
0
On peut restreindre ces ouverts tel que π(V ) = π(V ). On obtient donc un
0
diéomorphisme φ : V → V appelé glisser le long des feuilles.
Comme
x0
et
Proposition 120.
Revenons au cas d'un feuilletage quelconque.
γ : [0, 1] → L un chemin continue de x0 à x00 ,
et t0 = 0 < t1 < ... < tk = 1 une subdivision de [0, 1] tel que pour i = 1, ..., k
l'image de γ([ti − 1, ti ]) est contenue dans un ouvert feuilleté Ui .
Comme γ([ti − 1, ti ]) est connexe, γ([ti − 1, ti ]) est contenu dans une plaque
(L0 )i dans l'ouvert Ui .
Soit Ti une transversale à la variété feuilletée (Ui , FUi ) passant en xi = γ(ti ).
Glisser le long des feuilles dénit un diéomorphisme φi d'un voisinage ouvert
Vi−1 de xi−1 dans Ti−1 sur un voisinage ouvert Vi de xi dans Ti .
On a donc un diéomorphisme φk ◦ φk−1 ◦ ... ◦ φ1 d'un voisinage ouvert de
x0 dans T sur un voisinage ouvert de x00 dans T 0 .
Soient
121
Ce diéomorphisme sera encore appelé glisser le long de
γ
et parfois noté
holγ .
On appelle holonomie de
holγT,T
0
ou
holγ
γ
le germe de ce diéomorphisme qu'on notera
s'il n'y a pas d'ambiguïté.
Proposition 121.
γ vérie les propriétés suivantes :
γ ne dépend pas des transversales intermédiaires Ti .
(ii) L'holonomie de γ ne dépend pas de la chaîne d'ouverts feuilletés mais
uniquement du chemin γ .
(iii) L'holonomie de γ ne dépend que de la classe d'homotopie du chemin
γ à extrémités xées.
(iv) Si α est un autre chemin le long de la feuile L tel que α et γ soient
composables alors on a holαγ = holα holγ .
0
(v) Soient S une autre transversale en x0 et S une autre transversale en
0
0
0 ,S 0
T,T
S,T
S,S
T
x00 , alors holγ = holx¯0 ◦ holγ ◦ holx¯0 où x¯0 et x¯00 désignent les
L'holonomie de
(i) L'holonomie de
0
chemins constants en
Proposition 122.
Si
γ
x0
et
x00 .
est un lacet en
x0 ,
c'est-à-dire si
x00 = x0
et
T0 = T,
holγ laisse xe x0 .
holγ ne dépend que de la classe d'homotopie du chemin γ , on a donc
un morphisme de groupe π1 (L, x0 ) → Dif fx0 (T ) du groupe fondamental
de L en x0 vers le groupe des germes de diéomorphismes locaux de T qui
laissent xe x0 . L'image ce morphisme est un sous-groupe de Dif fx0 (T )
appelé le groupe d'holonomie de L en x0 .
On dit que le feuilletage F est sans holonomie si pour toute feuille le groupe
alors
Comme
d'holonomie est trivial.
Dénition 89.
On dit que deux chemins
α
et
γ
le long de la même feuille
et ayant les mêmes extrémités ont la même holonomie si
holα−1 γ = Id.
Cette relation est une relation d'équivalence sur l'ensemble des classes d'homotopie le long de la même feuille et ayant les mêmes extrémités. Les classes
d'équivalence seront appelées des classes d'holonomie.
Dénition 90.
(0)
où G
=X
On appelle groupoïde la donnée d'un couple
(G(1) , G(0) ),
γ:X→X
(1) est l'espace des èches
est l'espace des unités et G
munis des applications suivantes :
∆ : X → G(1) ,
(1) → G(1) ,
l'inverse i : G
(1)
l'image r : G
→ X,
(1) → X ,
la source s : G
(1)
(1)
la composition m : G2 →, où G2 est l'ensemble de paires d'éléments
0
(1)
0
composables (γ, γ ) dans G
, c'est-à-dire r(γ ) = s(γ).
l'inclusion
Les applications ci-dessus doivent vérier les propriétés suivantes :
r(∆(x)) = s(∆(x)),
et
m(u, ∆(s(u))) = u = m(∆(r(u)), u),
122
r(i(u)) = s(u) et m(u, i(u)) = ∆(r(u)), m(i(u), u) = ∆(s(u)),
s(m(u, v)) = s(v) et r(m(u, v)) = r(u),
m(u, m(v, w)) = m(m(u, v), w) si r(w) = s(v) et s(u) = r(v).
Dénition 91.
On appelle groupoïde d'holonomie de
GF où G(0) est la variété
M
(M, F)
le groupoïde
(1) est donné par les classes d'holonomie de
et G
chemin le long des feuilles.
L'inclusion est donnée par les classes d'holonomie de chemin constant, l'inverse et la composition sont donnés par l'inverse et la composition des chemins, et la source et l'image sont donnés par le point de départ et d'arrivée
du chemin.
A.4 Théorie de Molino
Nous allons rappeler maintenant deux théorèmes dûs à Pierre Molino qui
donnent la structure des feuilletages riemanniens. Pour plus de détails voir
[Mol88, MM03, EKAB84].
Théorème 42.
On suppose que le feuilletage
(M, F)
est transversalement
parallélisable, alors :
(i) Les adhérences des feuilles sont les bres d'une bration localement
triviale
W
π :M →W
appelée bration basique de
sera appelée la variété basique de
(ii) Il existe un groupe de Lie simplement connexe
F0
(M, F).
La variété
(M, F).
induit dans chaque adhérence de feuille
F
Γ tel que le feuilletage
Γ-feuilletage de
est un
Lie à feuilles denses.
Théorème 43. On suppose que F est transversalement orientable. Soit alors
SO(q) → M ] → M le bré principal des repères orthonormés transverses à
F . Le feuilletage F se relève sur M ] en un feuilletage F ] tel que :
]
(i) dim F = dim F
]
(ii) Le feuilletage F est transversalement parallélisable et invariant par
l'action du groupe H = SO(q).
]
De plus le parallélisme transverse à F se compose d'une partie verticale
(Q1 , ..., QN ) où N = q(q − 1)/2 = dim SO(q) formées des champs fonda]
mentaux de l'action de SO(q) sur M et d'une partie horizontale (P1 , ..., Pq )
donnée par la connexion de Levi-Civita transverse du bré principal
SO(q) → M ] → M .
Le parallélisme (P1 , ..., Pq , Q1 , ..., QN ) vérie :
(i) [Pi , Pj ] est vertical pour i, j = 1, ..., q ,
(ii) [Pi , Qk ] est horizontal pour i = 1, ..., q, k = 1..., N ,
(iii) [Qk , Ql ] est vertical pour k, l = 1, ..., N .
Remarque.
On peut toujours supposer quitte à passer à un revêtement à
deux feuillets que
(M, F)
est transversalement orientable (voir [MM03]).
123
Le théorème reste vrai si le feuilletage n'est pas transversalement orientable,
il sut de remplacer
SO(q)
par
O(q).
124
Annexe B
Notion de F -brés
Nous allons à présent étudier la notion de
F -brés
([KT75]) qui sera la
classe de brés vectoriels que nous considérerons par la suite. Nous commencerons par faire quelques rappels sur les connexions (voir [Spi79, GHV73,
KT68]). On désignera par
X
une variété.
Dénition 92. Soit P un bré principal au-dessus de X de groupe structural
G,
où
G
est un groupe de Lie compact.
P la donnée d'un sous-bré principal H tel que :
∀z ∈ H, Tz P = Vz ⊕ Hz où Hz désigne la bre de H en z .
(ii) ∀g ∈ G, ∀z ∈ P, Hzg = (Rg )∗ Hz où Rg est l'action à droite de g sur
P.
On appelle connexion sur
(i)
Dénition 93. Soit P un bré principal au-dessus de X de groupe structural
G,
où
G
est un groupe de Lie compact.
P la donnée d'un sous-bré principal H donné par
G-invariante ξ sur P à valeurs dans G l'algèbre de
On appelle connexion sur
le noyau d'une 1-forme
G.
∗
de ξ signie : (Rg ) (ξ) = Adg −1 (ξ).
Lie du groupe
L'invariance
Remarque.
Les deux dénitions précédentes sont en fait équivalentes (voir
[Spi79, GHV73]). Si
E
est le bré vectoriel associé à
P,
on alors une corres-
pondance biunivoque entre l'ensemble des connexions linéaires sur le bré
vectoriel
E
et l'ensemble des connexions sur le bré pincipal
Proposition 123.
Soient
connexion linéaire sur
E
P.
un bré vectoriel au-dessus de
X
et
∇
une
E.
Alors il existe une unique connexion linéaire
∇∗
sur
E∗
(notée encore
∇
n'y a pas d'ambiguïté) telle que
∀σ ∈ Γ(E), ∀σ ∗ ∈ Γ(E ∗ ), ∀X ∈ Ξ(M ),
h∇∗ (σ ∗ ), σi (X) + hσ ∗ , ∇(σ)i (X) = (d hσ ∗ , σi)(X).
De plus la courbure de
∇
est donnée par :
R∇∗ (X, Y )(σ ∗ ) = −R∇ (X, Y )∗ (σ ∗ ), ∀X, Y ∈ Ξ(M ), ∀σ ∗ ∈ Γ(E ∗ ).
125
s'il
Proposition 124.
Soient
E
et
E 0 des brés
E et E 0 .
vectoriels au-dessus de
X
et
∇, ∇0 des connexions linéaires sur
Alors il existe une unique connexion linéaire notée
∇ ⊗ ∇0
sur
E ⊗ E0
tel
que :
∇ ⊗ ∇0 (σ ⊗ σ 0 ) = ∇(σ) ⊗ σ 0 + σ ⊗ ∇(σ 0 ), ∀σ ∈ Γ(E), ∀σ ∈ Γ(E 0 ).
De plus la courbure de
∇ ⊗ ∇0
est donnée par :
R∇⊗∇0 = R∇ ⊗ Id + Id ⊗ R∇0 .
Proposition 125.
Soient
connexion linéaire sur
E
un bré vectoriel au-dessus de
X
et
∇
une
E.
Alors il existe une unique connexion linéaire
∇Λk
sur
Λk E
(notée encore
∇
s'il n'y a pas d'ambiguité) telle que :
∇Λk (σ1 ∧ ... ∧ σk ) =
k
X
σ1 ∧ ... ∧ ∇(σi ) ∧ ... ∧ σk , ∀σi ∈ Γ(E).
i=1
De plus la courbure de
∇Λ k
est donnée par :
R∇Λk (X, Y )(σ1 ∧ ... ∧ σk ) =
k
X
∀X, Y ∈ Ξ(M ), ∀σi ∈ Γ(E),
σ1 ∧ ... ∧ R∇ (X, Y )(σi ) ∧ ... ∧ σk .
i=1
Proposition 126. Soient E un bré vectoriel au-dessus de X , ∇ une connexion
linéaire sur
E,
et
γ
un chemin dans
X.
φ : R × Eγ(0) → E
γ : R → X tel que sur chaque bre φ est un isomorphisme et
φ] ◦ ∇ = d ◦ φ] où φ] est l'application induite par φ sur Γ(E).
L'isomorphisme φt : Eγ(0) → Eγ(t) est appelé transport parallèle le long de
γ de γ(0) à γ(t).
Alors il existe un unique morphisme de brés vectoriels
qui induit
Dénition 94.
vérie
Si
σ ∈ Γ(E),
on dit que
σ
est parallèle le long de
γ
si
σ
∇
une
φt (σγ(0) ) = σγ(t) .
Proposition 127.
Soient
E
un bré vectoriel au-dessus de
X
et
E . Alors on a :
γ1 et γ2 sont deux chemins composables, alors le transport parallèle
associé à γ1 γ2 est la composé du transport paralléle associé à γ1 et de
celui associé à γ2 .
(ii) Le transport parallèle associé à ∇ ne dépend que de la classe d'homotopie du chemin γ si et seulement si la courbure de ∇ est nulle
(c'est-à-dire la connexion ∇ est plate).
connexion linéaire sur
(i) Si
Démonstration.
Voir [KT68].
126
Proposition 128.
Soit
E
un bré vectoriel au-dessus de
X.
On suppose que les deux conditions suivantes sont vériées :
(i) pour tout chemin
γ
dans
X
et
∀t ∈ [0, 1],
on a un isomorphisme
φt : Eγ(0) → Eγ(t) ,
(ii) pour tout ouvert
U
de
Rn
U
M,
tel que
est convexe,
U
contient l'origine
et U est l'image d'une carte de
on note λx le chemin de U où
λx (t) = tx avec x ∈ U , alors l'application U → Gln (R) qui à x associe
∞
le transport parallèle associé à λx est C ,
alors il existe une unique connexion ∇ sur E tel que φt est le transport
parallèle le long de γ de γ(0) à γ(t).
De plus si γ est la courbe intégrale de X , ∇X est donnée par :
φ−1
t (σγ(0) ) − σγ(0)
.
t→0
t
∇X = lim
Démonstration.
Voir [KT68, Spi79].
Revenons à présent à notre variété
F.
P
M
munie d'un feuilletage riemannien
M de groupe structural G où G
p : P → M la projection.
On notera E le bré vectoriel associé à P .
Soit H une connexion sur P on notera ξ la 1-forme de connexion sur P à
valeurs dans l'algèbre de Lie G associée à H et ∇ la dérivée covariante sur
E associée à H . On rappelle que ∀z ∈ P , la submersion p induit un ismorphisme d'espace vectoriel de Hz sur Tp(z) M .
Soit
un bré principal au-dessus de
est un groupe de Lie compact et
Dénition 95.
feuilleté si
τ
Dans ce cas
On pose
τ = p∗ (T F).
τ
dénit un feuilletage
est invariant par l'action de
On dit que le bré vectoriel
G.
E est
F̃
Dénition 96.
P
est un
P
est
F -bré
associé est un
tel que dim(F)
= dim(F̃)
et
F̃
∇
est une connexion adaptée.
H
est basique si
ξ
est basique.
est feuilleté et admet une connexion basique, on dira
principal.
On dit que le bré vectoriel
E
est un
F -bré
vectoriel si le bré principal
F -bré et on dira dans ce cas que ∇ est une connexion basique.
Proposition 129.
∇,
P
feuilleté si le bré principal associé est un
On dit que la connexion
Si le bré principal
P
sur
bré feuilleté, et on dit dans ce cas que
que
On dit que le bré principal
est intégrable.
Si
E
est un bré vectoriel muni d'une connexion linéaire
alors :
E est un bré feuilleté si et seulement si sa courbure R∇ vérie
R∇ (U, V ) = 0, ∀U, V ∈ Γ(T F),
(ii) le bré E est un F -bré si et seulement si iV (R∇ ) = 0, ∀V ∈ Γ(T F).
(i) le bré
Démonstration.
Voir [KT75].
127
Exemple 23. Selon le théorème 12, νF muni de la connexion de Levi-Civita
transverse est un
F -bré.
Proposition 130.
Démonstration.
Donc
iV (R
∇∗
C'est-à-dire
Si
E
est un
F -bré
alors
E∗
et
Λk E ∗
sont des
F -brés.
E est un F -bré, on a iV (R∇ ) = 0, ∀V ∈ Γ(T F).
) = 0, ∀V ∈ Γ(T F) et iV (R∇∗ k ) = 0, ∀V ∈ Γ(T F).
E∗
Corollaire 16.
Comme
et
Λk E ∗
On note
Λ
sont des
F -brés.
νF ∗ = ν ∗ F . Alors ν ∗ F
et
Λk ν ∗ F
sont des
F -brés.
Dénition 97. Soient E un bré feuilleté au-dessus de M et ∇ une connexion
adaptée sur
Si
E.
α ∈ Γ(E), on dit que α est basique si ∀V ∈ Γ(T F), ∇V (α) = 0.
Γ(E/F) l'espace vectoriel des sections basiques.
On note
Remarque.
On voit immédiatement que
Exemple 24.
Γ(E/F) est un Ω0 (M/F)-module.
Les sections basiques du bré normal
νF ,
sont exactement
les champs de vecteurs basiques. En eet :
si
X
est tangent au feuilletage, la connexion de Levi-Civita transverse
est donné par la dérivée de Lie
LX ,
∇X
il sut alors d'utiliser la caractérisation
des champs basiques donnée par les propositions 35 et 36.
Proposition 131.
L'espace des sections basiques de
à l'espace des formes diérentielles basiques de degré
Démonstration.
Λk ν ∗ F
k.
est isomorphe
On a
Ωk (M/F) = {ω ∈ Ωk (M )/ iV (ω) = LV (ω) = 0, ∀V ∈ Γ(T F)},
k
donc Ω (M/F) ∼
= {ω ∈ Ωk (νF)/ LV (ω) = 0, ∀V ∈ Γ(T F)}.
∗
Montrons que ∀V ∈ Γ(T F), ∇V = LV .
∗
La connexion ∇ est caracterisée par :
∀V ∈ Γ(T F), ∀s ∈ Γ(νF), ∀s∗ ∈ Γ(ν ∗ F)
h∇∗ (s∗ ), si (V ) + hs∗ , ∇(s)i (V ) = (d hs∗ , si)(V ).
Donc on a
∇∗V (s∗ )(s) = −s∗ (∇V (s)) + V (s∗ (s))
= −s∗ (LV (s)) + V (s∗ (s))
= LV (s∗ )(s)
Donc
Donc
∀V ∈ Γ(T F), ∀ω ∈ Ωk (νF), LV (ω) = ∇∗V (ω).
Ωk (M/F) ∼
= {ω ∈ Ωk (νF)/ ∇∗V (ω) = 0, ∀V ∈ Γ(T F)}.
Proposition 132.
tées sur
E.
Alors
E un bré feuilleté et ∇, ∇0 des connexions adap∀σ ∈ Γ(E), ∀V ∈ Γ(T F), ∇V (σ) = ∇0V (σ).
Soient
En particulier la notion de section basique est indépendante du choix de la
connexion adaptée.
128
Démonstration.
Voir [KT75].
Dénition 98.
Soit
E un bré muni d'une métrique hermitienne h.
h comme une section du bré S 2 E ∗ des formes bilinéaires
symétriques sur E . La connexion basique ∇ sur E s'étend de manière natuS
2 ∗
relle en une connexion basique ∇ sur S E .
S
On dira que E est un F -bré hermitien si ∇V (h) = 0, ∀V ∈ Γ(T F).
On peut considérer
Proposition 133.
FE
sur
E
Démonstration.
TE
Si le bré
E est un F -bré hermitien, alors le
F est un feuilletage riemannien.
feuilletage
relevé du feuilletage
FE
q:E→M
Le bré normal à
tangent aux bres de
s'identie à la somme directe du bré
et du bré
q ∗ (νF)
métiques riemanniennes invariantes le long des feuilles de
129
qui sont munis de
FE .
Annexe C
Index
Cet index indique les pages où sont présentées les diérentes notions
introduites dans la thèse :
métrique quasi-brée : page 30,
connexion de Levi-Civita transverse : page 31 et page 32,
courbure principale : page 36,
forme diérentielle basique : page 37,
cohomologie basique : page 37,
forme volume transversale : page 44,
forme caractéristique : page 45,
espace de Sobolev basique : page 50 ,
opérateur diérentiel basique : pages 51 et 52,
opérateur diérentiel basique transversalement elliptique : page 52,
indice basique : page 60,
Laplacien basique : page 61,
caractéristique d'Euler basique : page 68,
signature basique : page 70,
indice distributionnel basique : page 103,
F -bré
: page 127,
connexion basique : page 127.
130
Bibliographie
[AL92]
J. A. Alvarez Lopez.
The basic component of the mean cur-
vature of riemannian foliations.
Geometry, 10 :179194, 1992.
[AS68]
Annals of Global Analysis and
M.F. Atiyah and I.M. Singer. The index of elliptic operators :
The Annals of Mathematics, 87(3) :546604, 1968.
M.F. Atiyah. Elliptic operators and compact groups.
3.
[Ati]
Lecture
Notes in Math. 401.
[BGV04]
N. Berline, E. Getzler, and M. Vergne.
operators.
Heat kernels and Dirac
Grundlehren text Editions. Springer-Verlag, Berlin,
2004.
[BKR10a]
J. Brüning, Franz F. W. K., and K. Richardson. Index theory
for basic dirac operators on riemannian foliations.
Preprint,
2010.
[BKR10b]
J. Brüning, Franz F. W. Kamber, and K. Richardson.
The
equivariant index theorem for tansversally elliptic operators and
the basic index theorem for riemannian foliations.
Preprint,
2010.
[BV96a]
N. Berline and M. Vergne.
The chern character of a trans-
versally elliptic symbol and the equivariant index.
Mathematicae, 124(1) :1149, 1996.
[BV96b]
N. Berline and M. Vergne.
Inventiones
L'indice équivariant des opéra-
teurs transversallement elliptiques.
Inventiones Mathematicae,
124(1) :51101, 1996.
Astérisque, 116 :3152, 1984.
Foliations 1, volume 23 of Graduate
[Car84]
Y. Carrière. Flots riemanniens.
[CC00]
A. Candel and L. Conlon.
Studies in Mathematics.
American Mathematical Society, Wil-
mington, DE, 2000.
[Dom98]
D.
Dominguez.
riemannian
Finiteness
and
tenseness
theorems
for
American Journal of Mathematics,
foliations.
120(6) :12371276, 1998.
[Duf ]
M. Duo.
Opérateurs transversalement elliptiques et formes
diérentielles équivariantes.
131
[EKA90]
A. El Kacimi-Alaoui. Opérateurs transversalement elliptiques
sur un feuilletage riemannien et applications.
thematica, 73(1) :57106, 1990.
[EKAB84]
A. El Kacimi-Alaoui and R. Barre.
thematics Lecture Series.
Compositio Ma-
Foliations, volume 11 of Ma-
Publish or Perish Inc., Wilmington,
DE, 1984.
[EKAH86]
A. El Kacimi-Alaoui and G. Hector. Décomposition de Hodge
basique pour un feuilletage riemannien.
Fourier, 36(3) :207227, 1986.
[EKAN93]
A. El Kacimi Alaoui and M. Nicolau.
variance of the basic cohomology.
Annales de l'institut
On the topological in-
Mathematische Annalen,
295 :627634, 1993.
[EKASH85] A. El Kacimi-Alaoui, V. Sergiescu, and G. Hector. La cohomologie basique d'un feuilletage riemannien est de dimension nie.
[Far06]
Mathematische Zeitschrift, 188 :593599, 1985.
J. Faraut. Analyse sur les groupes de Lie. Calvage et Mounet,
2006.
[GHV73]
[Gil84]
[GL10]
W. Greub, S. Halperin, and R. Vanstone.
Connections, curof Pure and applied
vature, and cohomology vol2, volume 47-2
Mathematics. Academic Press, 1973.
P. B. Gilkey. Invariance theory, the heat equation, and the
Atiyah-Singer index theorem, volume 11 of Mathematics Lecture Series. Publish or Perish Inc., Wilmington, DE, 1984.
A. Gorokhovsky and J. Lott. The index of a transverse dirac
type operator : the case of abelain molino sheaf.
[Hae58]
Preprint, 2010.
A. Haeiger. Structures feuilletées et cohomologie à valeur dans
un faisceau de groupoïdes.
Commentarii Mathematici Helvetici,
32(1) :248329, 1958.
[Hae88]
[Hel01]
A. Haeiger. Leaf closures in riemannian foliations.
A Fête of
Topology, Academic Press, Boston, MA, pages 332, 1988.
S. Helgason. Dierential Geometry, Lie Groups, and Symmetric
Spaces, volume 34 of Graduate Studies in Mathematics. American Mathematical Society, 2001.
[Hir78]
F.E.P. Hirzebruch.
Topological methods in algebraic geometry.
Springer-Verlag, 1978.
[KT68]
F.W. Kamber and P. Tondeur.
Flat manifolds.
Lecture Notes
in Math. 67. Springer-Verlag, 1968.
[KT75]
F.W. Kamber and P. Tondeur.
teristic classes.
Foliated bundles and charac-
Lecture Notes in Math. 493. Springer-Verlag,
1975.
132
[KT87]
F. Kamber and P. Tondeur.
De Rahm-Hodge theory for rie-
Math. Ann., pages 415431, 1987.
Lawson and M.-L. Michelsohn. Spin Geometry.
mannian foliations.
[LM89]
H. Blaine Jr.
Princeton university press, 1989.
[Mas92]
[MM03]
[Mol88]
[MS74]
X. Masa. Duality and minimality in riemannian foliations.
Com-
ment. Math. Helvetici, 67 :1727, 1992.
I. Moerdijk and J. Mrcun. Introduction to foliations and Lie
groupoids, volume 91 of Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge, 2003.
P. Molino. Riemmannian foliations, volume 73 of Progress in
Mathematics. Birkhauser Boston, Inc., Boston, 1988.
J. Milnor and J. D. Stashe. Characteristic classes, volume 76
of Annals of Mathematics Studies. Princeton University Press,
Princeton ; Tokyo University Press, Tokyo, 1974.
[Nov63]
SP Novikov. Topology of foliations.
Trans. Moscow Math. Soc,
14 :268305, 1963.
[NRT90]
S. Nishikawa, M. Ramachandran, and P. Tondeur.
equation for riemmanian foliations.
The heat
Transactions of the Ameri-
can Mathematical Society, 319(2) :619630, 1990.
[PR96]
E. Park and K. Richardson. The basic laplacian of a riemannian
foliation.
American Journal of Mathematics,
118 :12491275,
1996.
The
[Rei59a]
B.L. Reinhart. Foliated manifolds with bundle-like metrics.
[Rei59b]
B.L. Reinhart. Harmonic integrals on foliated manifolds.
[Ric98]
K. Richardson. The asymptotics of heat kernels on riemannian
Annals of Mathematics, 69(1) :119132, 1959.
rican Journal of Mathematics, 81(2) :529536, 1959.
Geometric and Functional Analysis, 8(2), 1998.
foliations.
[Ric10]
Ame-
K. Richardson.
Traces of heat operators on riemannian folia-
Trans. Amer. Math. Soc., 362(5), 2010.
Roe. Elliptic operators, topology and asymptotic methods.
tions.
[Roe98]
J.
Chapman & Hall/CRC, 1998.
[Rum79]
H. Rummler.
Quelques notions imples en géométries rieman-
niennes et leurs applications aux feuilletages compacts.
ment. Math. Helvetici, 54 :224239, 1979.
[Ser85]
V. Sergiescu.
Cohomologie basique et dualité des feuilletages
Annales de l'institut Fourier, 35(3) :137158, 1985.
A comprehensive introduction to dierential geome-
riemanniens.
[Spi79]
M. Spivak.
try vol 2.
Com-
Publish or Perish, Inc, 1979.
133
[Thu74]
W. Thurston. The theory of foliations of codimension greater
than one.
Commentarii Mathematici Helvetici, 49(1) :214231,
1974.
[Ton97]
[Wel80]
P. Tondeur. Geometry of Foliations, volume 90 of Monographs
in Mathematics. Birkhauser Verlag, 1997.
R.O.N. Wells. Dierential analysis on complex manifolds. Springer, 1980.
134