Activité sur l`étude d`un saut en parachute

Etude d’un mouvement : le saut en parachute le plus haut du monde
Situation déclenchante projeter la video youtube du reportage de
France 24 : http://www.youtube.com/watch?v=Rfl89gQkak0
Le 14 octobre 2012, La mission « Red Bull Stratos » permit à l’Autrichien Félix Baumgartner de sauter en
chute libre depuis une nacelle située à 39km d'altitude, en pleine stratosphère. Ce saut fait de lui le premier
homme à franchir le mur du son sans assistance mécanique. Dans sa chute libre, qui a duré 4 min 19 s,
l'Autrichien de 43 ans a atteint une vitesse maximale de 1342 km/h. C'est aussi le saut en parachute le plus haut
jamais effectué.
Son ballon s’est donc élevé jusqu’à la stratosphère où l’atmosphère est environ 500 fois moins dense qu’au
niveau du sol. Malgré sa très grande vitesse, l’action des frottements de l’air sur le parachutiste a été moins
importante durant la première phase de la chute ce qui a permis à Félix Baumgartner de battre le record de
vitesse de Joseph Kittinger qui datait de 1960 avec 988 km/h pour un saut de 30000 m d’altitude.
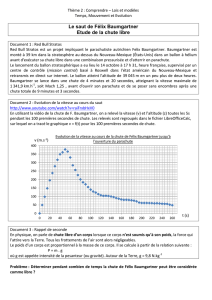
Au cours de la première phase de son saut, on repère la position de Baumgartner
sur un axe Ox. L’origine 0 de l’axe correspondant au point de départ du saut à t = 0 s.
En négligeant les frottements de l’air, l’évolution de la position du parachutiste
au cours du temps serait celle représentée sur le graphique suivant qui répond
à l’équation horaire :
²gt
2
1
)t(x 
avec g l’intensité de la pesanteur dont on prendra pour
valeur 9,8N.kg-1.
a) Calculer le temps mis par Baumgartner pour faire une chute de 6000 m depuis sa nacelle
Vérifier cette valeur graphiquement.
Document a :
0
x

b) A l’aide des informations précédentes et des documents ci-dessous, nous allons essayer de déterminer au
bout de combien de temps Baumgartner a atteint la vitesse instantanée de son record c'est-à-dire 1342 km.h-1.
Définition : la vitesse instantanée v(t) du point G ou vitesse de G tout court est égale à la vitesse moyenne
entre deux positions infiniment proches.
Documents b : exemple d’un mouvement décéléré
m
m
t
x
Vmoyenne 

Document c : extrait du cours de votre professeur de mathématiques :
…
2 ) Nombre dérivé d’une fonction en un point
Def : On appelle nombre dérivé de la fonction f au point a, la limite, si elle existe, du taux de variation entre a et a+h,
quand h tend vers 0. Cette limite, notée f ’(a) vérifie : .
…
4 ) Tangentes
Prop : Si f est dérivable en a, alors Cf admet au point A une tangente (T) de pente f ’(a).
Plus précisément, l’équation de (T) est : y = f ’(a)(x - a) + f(a).
b.1) Application : en vous appuyant sur les informations précédentes, calculer la vitesse instantanée du
parachutiste à t = 20s.
b.2) En généralisant, quelle est la relation qui lie la vitesse instantanée v(t) à un instant t, f’(t) et
dt
dx
(t) ?
b.3) A l’aide de l’équation horaire et des informations précédentes déterminer au bout de combien de temps
Baumgartner a atteint la vitesse record de 1342 km.h-1.
)t(
dt
dx
)t(v 22 
La vitesse instantanée
à t2

c) Choix de l’altitude du saut
A l’aide du document précédent, proposer une explication justifiant le choix de l’altitude de départ pour le saut
par Félix Baumgartner qui lui a permis de battre le record du monde de la plus haute altitude de saut en
parachutisme.