La loi de Wien

Image Partie 2 / Les couleurs de la lumière et de la matière
Activité
expérimentale Les spectres lumineux des corps chauds
▪ Nous sommes entourés de diverses sources de lumière, les étoiles et les lampes utilisées dans la vie
courante : lampe à incandescence (lampes de chevet), lampe fluorescente (lampes à « économie
d’énergie » des plafonniers des maisons, « néons » des salles de classes), lampe halogène, lampe à
vapeur de sodium (éclairage public)…
▪ Pour observer les lumières émises par ces sources de lumières, on dispose, en premier de notre œil,
mais également de prismes, de réseaux, de spectroscopes (dispositifs plus complets, comportant une
fente et un réseau, ou éventuellement un prisme)
 Dans ce TP, on s’intéresse aux lumières émises par les corps (solides, liquides ou gaz) portés à
haute température
Lumière émise par une lampe à incandescence
- Brancher une lampe aux bornes d’un généra-
teur puis faire varier l’intensité du courant tra-
versant la lampe.
 Qu’observe-t-on ?
- Observer maintenant à l’aide d’un réseau ou
d’un spectroscope, la lumière émise par le fila-
ment bien blanc
 Qu’observe-t-on ?
 Dessiner le spectre observé lorsque le fila-
ment fortement chauffé est blanc (T = 2700K)
 Comment peut-on qualifier ce genre de spec-
tre ?
- Observer à l’aide d’un réseau ou
d’un spectroscope, la lumière émise par le fila-
ment très faiblement éclairé
 Qu’observe-t-on ?
 Dessiner le spectre observé lorsque le fila-
ment faiblement chauffé est rouge (T=1500 K)
 Que peut-on conclure sur les spectres des
lumières émises par les corps chauds ?
Vers la loi de Wien...
Températures de surface des étoiles
▪ Bételgeuse et Bellatrix sont deux étoiles ap-
partenant à la constellation d’Orion qui est très
facilement visible dans le ciel des nuits d’hiver
La température de surface est de 3 500 K pour
Bételgeuse et de 28 000 K pour Bellatrix.
 D’après ces données et de ce qui a été vu
précédemment sur la couleur du filament chauf-
fé de la lampe à incandescence, quelle devrait-
être la couleur de ces étoiles?
 Comment peut-on expliquer les couleurs réel-
les de Bételgeuse et de Bellatrix (rouge pour
Bételgeuse et bleue pour Bellatrix) ?
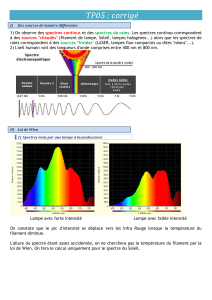
Le profil spectral
Le graphe suivant
représente l’intensité
lumineuse émise en
fonction de la lon-
gueur d’onde pour des
corps de températures
différentes.

▪ Pour étudier plus en profondeur la lumière
émise par une source lumineuse, on ne peut pas
se contenter de l’observation de son spectre. On
utilise son profil spectral (relevé par des détec-
teurs électroniques).
▪ Ce profil spectral est une courbe représentant
l’intensité de la lumière émise par la source
en fonction de
la longueur d’onde.
 Quelle est la longueur d’onde correspondant
au maximum d’intensité lumineuse à 3500K ? à
5000 K ?
 De manière générale, que peut-on dire de la
longueur d’onde de la radiation la plus intense
lorsque la température augmente ?
La loi de Wien
▪ Dans le tableau ci-dessous, il est donné, pour
plusieurs températures en Kelvin, la valeur de la
longueur d’onde correspondant au maximum
d’émission lumineuse du corps chauffé.
T (K) 2500 3500 4500 5500 6500
λM (nm) 1156 826 642 526 445
7500 8500 9500 10500 11500
385 345 305 275 251
12500 13500 14500 15500 16500
231 214 200 186 175
17500 18500 19500
165 156 148
 A l’aide d’un tableur, recopier ces données et
tracer la courbe 
 T
1
f
M
avec λM en m et T en K
 Que remarque-t-on?
 En déduire une relation entre la longueur
d’onde λM et l’inverse de température.
 Enoncer la loi de Wien
Applications en astronomie
► Application 1
Le profil spectral d'une étoile est représenté ci-
dessous.
 Evaluer λmax, la longueur d'onde de la radia-
tion lumineuse la plus intense émise par cette
étoile.
 En appliquant la loi de Wien, donner une es-
timation de la température de surface de cette
étoile.
► Application 2
Bételgeuse Soleil Bellatrix
Température
de surface 3 500 K 5500 K 28 000 K
λM (nm)
 Calculer la longueur d’onde de la radiation
lumineuse la plus intense pour ces 3 étoiles.
 Associer aux trois étoiles, un des trois spec-
tres ci-dessous
 Conclure sur la couleur de ces étoiles.
 Quels sont les paramètres dont dépend la
couleur d’une étoile ?